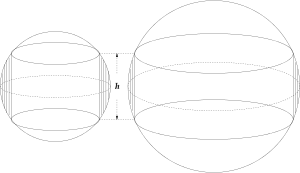
Problème du rond de serviette

Une version de ce problème est posée au XVII^e siècle dans les mathématiques japonaises par Seki Kōwa. D'après Smith et Mikami 1914, Seki appelait le solide un « anneau-arc (arc-ring, kokan ou kokwan en japonais).

Schéma illustrant les différentes variables.

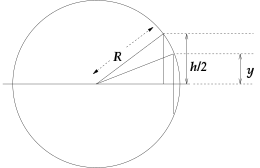
On suppose un cylindre dont l'axe passe par le centre d'une boule de rayon ${\displaystyle R}$. ${\displaystyle h}$ représente la hauteur (distance parallèle à l'axe) de la partie du cylindre située à l'intérieur de la boule. La « bande » est la partie de la boule située en dehors du cylindre.

D'après le théorème de Pythagore, le rayon du cylindre est :

${\displaystyle {\sqrt {R^{2}-\left({\frac {h}{2}}\right)^{2}}},\qquad \qquad (1)}$

le rayon d'une coupe transversale horizontale de la boule à une hauteur ${\displaystyle y}$ au-dessus de l'« équateur » de la boule est :

${\displaystyle {\sqrt {R^{2}-y^{2}}}.\qquad \qquad (2)}$

La coupe transverse (en) de la bande avec le plan à la hauteur ${\displaystyle y}$ est la région située à l'intérieur du grand cercle dont le rayon est donné en (2) et à l'extérieur du petit cercle dont le rayon est donnée en (1). L'aire de la coupe est donc l'aire du plus grand cercle moins celle du petit cercle :

${\displaystyle {\begin{aligned}&{}\quad \pi ({\text{grand rayon}})^{2}-\pi ({\text{petit rayon}})^{2}\\&=\pi \left({\sqrt {R^{2}-y^{2}}}\right)^{2}-\pi \left({\sqrt {R^{2}-\left({\frac {h}{2}}\right)^{2}\,{}}}\,\right)^{2}=\pi \left(\left({\frac {h}{2}}\right)^{2}-y^{2}\right).\end{aligned}}}$

On remarque que ${\displaystyle R}$ n'apparaît plus dans l'expression. L'aire de la coupe transverse à une hauteur ${\displaystyle h}$ ne dépend donc pas de ${\displaystyle R}$, tant que ${\displaystyle y}$ ≤ ${\displaystyle h}$/2 ≤ ${\displaystyle R}$.

Le volume de la bande est :

${\displaystyle \int _{-h/2}^{h/2}({\text{aire de la coupe à la hauteur }}y)\,dy,}$

qui lui non plus ne dépend pas de ${\displaystyle R}$.

Cela est une application de la méthode des indivisibles. Puisque l'aire de la coupe est la même que celle d'une sphère de rayon ${\displaystyle h}$/2, le volume est :

${\displaystyle {\frac {4}{3}}\pi \left({\frac {h}{2}}\right)^{3}={\frac {\pi h^{3}}{6}}.}$

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Napkin ring problem » (voir la liste des auteurs).

• (en) Keith Devlin, « The Napkin Ring Problem » [archive du 11 août 2011], Mathematical Association of America, 2008
• (en) Keith Devlin, « Lockhart's Lament » [archive du 11 août 2011], Mathematical Association of America, 2008
• (en) Martin Gardner, My best mathematical and logic puzzles, Dover Publications, 1994, « Hole in the Sphere », p. 8
• (en) Samuel I. Jones, Mathematical Wrinkles for Teachers and Private Learners, Norwood, MA, J. B. Cushing Co., 1912 Problem 132 asks for the volume of a sphere with a cylindrical hole drilled through it, but does not note the invariance of the problem under changes of radius.
• (en) Mark Levi, The Mathematical Mechanic : Using Physical Reasoning to Solve Problems, Princeton University Press, 2009, 102–104 p. (ISBN 978-0-691-14020-9, lire en ligne), « 6.3 How Much Gold Is in a Wedding Ring? ». Levi argues that the volume depends only on the height of the hole based on the fact that the ring can be swept out by a half-disk with the height as its diameter.
• (en) L. Lines, Solid geometry : With Chapters on Space-lattices, Sphere-packs and Crystals, Dover, 1965. Reprint of 1935 edition. A problem on page 101 describes the shape formed by a sphere with a cylinder removed as a "napkin ring" and asks for a proof that the volume is the same as that of a sphere with diameter equal to the length of the hole.
• (en) George Pólya, Mathematics and Plausible Reasoning, Vol. I: Induction and Analogy in Mathematics, Princeton University Press, 1990, 191–192 p.. Reprint of 1954 edition.
• (en) David E. Smith et Yoshio Mikami, A History of Japanese Mathematics, Open Court Publishing Company, 1914, 121–123 p. (lire en ligne). Republished by Dover, 2004, (ISBN 0-486-43482-6). Smith and Mikami discuss the napkin ring problem in the context of two manuscripts of Seki on the mensuration of solids, Kyuseki and Kyuketsu Hengyo So.

• (en) Eric W. Weisstein, « Spherical Ring », sur MathWorld
• (en) [vidéo] The Napkin Ring Problem sur YouTube