Mathématiques japonaises
Les mathématiques japonaises (和算, wasan) concernent les méthodes et résultats mathématiques développés au Japon durant l’époque d'Edo (1603-1867). Le terme Wasan, de Wa signifiant « Japon » et San, « mathématiques », est un néologisme créé dans les années 1870[1] par opposition au terme yosan désignant les théories occidentales[2].
Dans l’histoire des mathématiques, le développement des wasan n'entre pas dans le développement des théories occidentales et propose des solutions alternatives. Mais les wasan ne sont progressivement plus utilisées au début de l’ère Meiji (1868–1912) avec l’ouverture du Japon à la culture occidentale et l’adoption par les mathématiciens japonais des mathématiques occidentales.
Histoire
Cette approche des mathématiques a évolué durant une période où le Japon était coupé de l’influence européenne. Mōri Kambei est le premier mathématicien japonais connu[3]. Il est professeur de mathématiques et compte parmi ses élèves Yoshida Mitsuyoshi, Imamura Chisho et Takahara Kisshu. Ces trois personnages seront identifiés plus tard comme les trois arithméticiens[4].
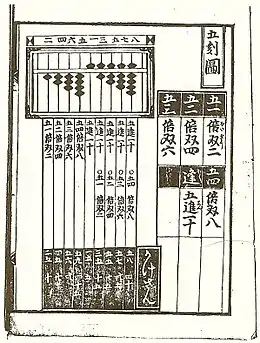
Yoshida est l’auteur du plus ancien texte mathématique japonais qui nous soit parvenu. Cette œuvre de 1627 s'appelle Jinkoki et traite de l’arithmétique soroban[5].
Seki Kōwa (1642-1708) développe le calcul différentiel à la même époque que les Européens[6] et invente vers 1680 la méthode d'accélération de convergence appelée Delta-2 et attribuée à Alexander Aitken qui l'a redécouverte en 1926 et popularisée[7].
Mathématiciens notables
- Mōri Kambei (début du XVIIe siècle), développe des méthodes arithmétiques pour l'emploi du soroban (boulier japonais)
- Yoshida Mitsuyoshi (1598–1672)
- Seki Takakazu (1642–1708), principe du cercle (enri), qui représente une forme brute de calcul intégral
- Takebe Kenkō (1664–1739)
- Matsunaga Ryohitsu (fl. 1718-1749)[8]
- Kurushima Kinai (d. 1757)
- Arima Raido (1714–1783)[9]
- Ajima Naonobu (1739–1783)
- Fujita Sadasuke (1734-1807)
- Aida Yasuaki (1747–1817)
- Sakabe Kōhan (1759–1824)
- Hasegawa Ken (c. 1783-1838)[9]
- Wada Nei (1787–1840)
- Shiraishi Nagatada (1796–1862)[10]
- Koide Chōjūrō (1797–1865)[9]
- Omura Isshu (1824–1871)[9]
Notes et références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Japanese mathematics » (voir la liste des auteurs).
- Selin, Helaine. (1997). Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures, p. 641. sur Google Livres
- Smith, David et al. (1914). A History of Japanese Mathematics, p. 1 n2. sur Google Livres
- Campbell, Douglas et al. (1984). Mathematics: People, Problems, Results, p. 48.
- Smith, p. 35. sur Google Livres
- Restivo, Sal P. (1984). Mathematics in Society and History, p. 56. sur Google Livres
- Smith, pp. 91-127. sur Google Livres
- Claude Brezinski. Convergence acceleration during the 20th century. J. Comput. Appl. Math, 122:1–21, 2000.
- Smith, pp. 104, 158, 180. sur Google Livres
- List of Japanese mathematicians - - Université Clark, Dept. of Mathematics and Computer Science
- Smith, p. 233. sur Google Livres
Bibliographie
- Campbell, Douglas M. et John C. Iggins. (1984). Mathematics: People, Problems, Results. Belmont, California: Warsworth International. (ISBN 0534032001 et 9780534032005); (ISBN 053403201X et 9780534032012); (ISBN 0534028799 et 9780534028794); OCLC 300429874
- Endō Toshisada (1896). History of mathematics in Japan (日本數學史史, Dai Nihon sūgakush). Tōkyō: _____. OCLC 122770600
- Fukagawa, Hidetoshi, et Daniel Pedoe. (1989). Japanese temple geometry problems = Sangaku. Winnipeg: Charles Babbage. (ISBN 0919611214 et 9780919611214); OCLC 474564475
- __________ et Daniel Pedoe. (1991) How to resolve Japanese temple geometry problems? (日本の幾何ー何題解けますか?, Nihon no kika nan dai tokemasu ka) Tōkyō : Mori Kitashuppan. (ISBN 4627015305 et 9784627015302); OCLC 47500620
- __________ et Tony Rothman. (2008). Sacred Mathematics: Japanese Temple Geometry. Princeton: Princeton University Press. (ISBN 9780691127453 et 069112745X); OCLC 181142099
- Horiuchi, Annick. (1994). Les Mathématiques japonaises à l’époque d’Edo (1600–1868) : Une Étude des travaux de Seki Takakazu (?-1708) et de Takebe Katahiro (1664–1739). Paris : Librairie Philosophique J. Vrin. (ISBN 2711612139 et 9782711612130) ; OCLC 318334322
- Kobayashi, Tatsuhiko. (2002) What kind of mathematics and terminology was transmitted into 18th-century Japan from China?, Historia Scientiarum, vol. 12, no 1.
- Kobayashi, Tatsuhiko. Trigonometry and Its Acceptance in the 18th-19th Centuries Japan.
- Morimoto, Mitsuo. Infinite series in Japanese Mathematics of the 18th Century.
- Morimoto, Mitsuo. A Chinese Root of Japanese Traditional Mathematics – Wasan
- Ogawa, Tsukane. A Review of the History of Japanese Mathematics. Revue d’histoire des mathématiques 7, fascicule 1 (2001), 137-155.
- Restivo, Sal P. (1992). Mathematics in Society and History: Sociological Inquiries. Dordrecht: Kluwer Academic Publishers. (ISBN 0792317653 et 9780792317654); OCLC 25709270
- Selin, Helaine. (1997). Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures. Dordrecht: Kluwer/Springer. (ISBN 0792340663 et 9780792340669); OCLC 186451909
- David Eugene Smith et Yoshio Mikami. (1914). A History of Japanese Mathematics. Chicago: Open Court Publishing. OCLC 1515528; see online, multi-formated, full-text book at archive.org
Articles connexes
- Sangaku, des énigmes géométriques japonaises de géométrie euclidienne gravées sur des tablettes de bois
- Soroban, un boulier japonais
- Catégorie:Mathématicien japonais
Liens externes
- (en) Sangaku
- « Les mathématiques japonaises : Entretien avec Marion Cousin », sur blogs.mediapart,
- (en) Kümmerle, Harald. Bibliography on traditional mathematics in Japan (wasan)