Paradoxe d'Achille et de la tortue
Le paradoxe d'Achille et de la tortue, formulé par Zénon d'Élée, dit qu'un jour, le héros grec Achille a disputé une course à pied avec une tortue. Comme Achille était réputé être un coureur très rapide, il avait accordé gracieusement au lent reptile une avance de cent mètres.
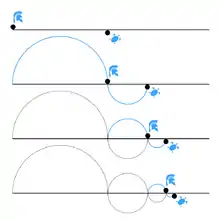
L'argument exposé par Zénon est qu'Achille ne pourra pas rattraper la tortue si celle-ci a de l'avance sur lui, et ce, quelle que soit sa vitesse (non nulle) ; car pendant qu'Achille court jusqu'au point d'où a démarré la tortue, cette dernière avance, de telle sorte qu'Achille ne pourra jamais annuler l'avance de l'animal.
Argument énoncé par Zénon
Zénon d'Élée affirme donc que le rapide Achille n'a jamais pu rattraper la tortue[2] - [3]. En effet, supposons pour simplifier le raisonnement que chaque concurrent court à vitesse constante, l'un très rapidement et l'autre très lentement : au bout d'un certain temps, Achille aura comblé ses cent mètres de retard et atteint le point de départ de la tortue ; mais pendant ce temps, la tortue aura parcouru une certaine distance, certes beaucoup plus courte mais non nulle, disons un mètre. Cela demandera alors à Achille un temps supplémentaire pour parcourir cette distance, pendant lequel la tortue avancera encore plus loin, puis une autre durée avant d'atteindre ce troisième point alors que la tortue aura encore progressé. Ainsi, toutes les fois qu'Achille atteint l'endroit où la tortue se trouvait, elle se retrouve encore plus loin. Par conséquent, le rapide Achille n'a jamais pu et ne pourra jamais rattraper la tortue.
Résolution du paradoxe
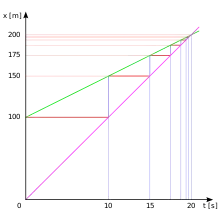
Pour simplifier la résolution, on choisit arbitrairement les valeurs suivantes : Achille se déplace à 10 m/s (proche du record du monde du 100 mètres au XXe siècle), la tortue à 5 m/s (peu vraisemblable mais rend le graphique plus lisible) et la tortue a 100 mètres d'avance sur Achille.
Avec une série
Dans le paradoxe de Zénon, on calcule la durée de l'événement « Achille rattrape la tortue » en additionnant tous les événements de type « Achille parcourt la distance jusqu'à la position actuelle de la tortue ». Or, ces durées sont de plus en plus petites, mais jamais égales à zéro, et leur nombre est infini.
L'erreur mathématique était de dire « donc Achille ne rattrape jamais la tortue », car l'analyse moderne démontre qu'une série infinie de nombres strictement positifs peut converger vers un résultat fini.
Avec les vitesses 10 m/s pour Achille et 5 m/s pour la tortue qui a 100 m d'avance, la première étape prend 10 secondes, la suivante 5 secondes, etc. On obtient la série suivante : T = 10 + 5 + 2,5 + 1,25 + … Finalement, la durée exacte est : 20 secondes.
Plus formellement, la somme des étapes s'écrit :
C'est la somme d'une série géométrique. On utilise le résultat général :
La série géométrique réelle de terme initial et de raison est convergente, et sa somme vaut :
Et l'on trouve ici :
Par résolution d'équation
On peut éviter les additions infinies en cherchant non pas à faire rattraper la tortue là où elle se trouve, mais en cherchant à quel moment Achille et la tortue seront au même point. Formellement, on cherche T tel que , ce qui donne .
On retrouve ainsi .
Équivalence graphique
Le graphique plus haut donne les positions respectives d'Achille et de la tortue.
La somme de l'infinité des termes de la série revient à suivre les lignes verticales rouges et horizontales bleues jusqu'à trouver un point de rencontre. La résolution de l'équation revient à chercher directement l'intersection des lignes « Achille » et « tortue ».
Sur l'existence de l'infiniment petit
On notera aussi qu'à travers ce paradoxe, existe une volonté de montrer que l'infiniment petit n'existe pas. Pensée également partagée par Démocrite, l'inventeur de la notion d'atome. La physique quantique va elle aussi dans ce sens en admettant l'existence d'une unité de temps et d'une unité de taille toutes deux indivisibles — approximativement e–44 s et e–35 m (unités de Planck).
Si l'on utilise cette limite, il n'est plus possible de découper en une infinité d'étapes : on additionne donc un nombre fini de durées finies (non infiniment petites), et le total est une durée finie. Cependant, la résolution mathématique démontre bien que la durée reste finie même en acceptant le découpage en une infinité d'étapes, et donc cet exercice de pensée ne réfute pas l'existence de l'infiniment petit.
Notes et références
- Cet article est partiellement ou en totalité issu de l'article intitulé « Paradoxes de Zénon » (voir la liste des auteurs).
- Grandjean, Martin (2014) Henri Bergson et les paradoxes de Zénon : Achille battu par la tortue ?
- Aristote (trad. Jules Barthélemy-Saint-Hilaire), Physique, Paris, Ladrange, Durand, (lire en ligne), « Livre VI, chapitre 14, § 4 » : « Le second sophisme de Zénon est celui qu'on appelle l'Achille. Il consiste à dire que jamais le plus lent, quand il est en marche, ne pourra être atteint par le plus rapide, attendu que le poursuivant doit, de toute nécessité, passer d'abord par le point d'où est parti celui qui fuit sa poursuite, et qu'ainsi le plus lent conservera constamment une certaine avance. » (IVe siècle av. J.-C.).
- (en) Simplicius (trad. David Konstan), On Aristotle Physics 6, Londres, Bloomsbury, , 181 p. (ISBN 978-0-7156-2217-9, lire en ligne), chap. 1014-1015 (vers 533-538 apr. J.-C.)
Voir aussi
Articles connexes
Liens externes
- Notices dans des dictionnaires ou encyclopédies généralistes :


![{\displaystyle q\in \left]-1,1\right[}](https://img.franco.wiki/i/efdd8603bc8d056e3f777774e57957e72714a5ed.svg)




