Ordinateur quantique de Kane
L'architecture de Kane pour la réalisation de l'ordinateur quantique est une proposition théorique suggérant l'utilisation des spins nucléaires d'atomes donneurs uniques de 31P dans un cristal de silicium isotopiquement pur (28Si) comme composants de base (qubits).
Historique
L'architecture de Kane a été proposée par B. E. Kane en 1997[1]. Le premier pas vers la réalisation de l'architecture fut la démonstration du positionnement d'un dopant unique de phosphore avec une précision d'un site atomique par lithographie à l'hydrogène assistée par STM en 2011[2]. Une autre étape importante fut la démonstration du contrôle quantique complet du spin d'un électron piégé par l'atome de phosphore[3] et du spin du noyau[4] en 2012. L'intégration de tous les composants nécessaires à un processeur quantique pleinement fonctionnel pose encore un grand défi technologique en 2013.
Fonctionnement
Système physique
L'architecture consiste en un réseau bi-dimensionnel de dopants de 31P dans un cristal hôte de 28Si séparés par une distance d'environ 10 à 20 nm et enfoui à la même profondeur sous une interface silicium-oxyde de silicium (SiO2).
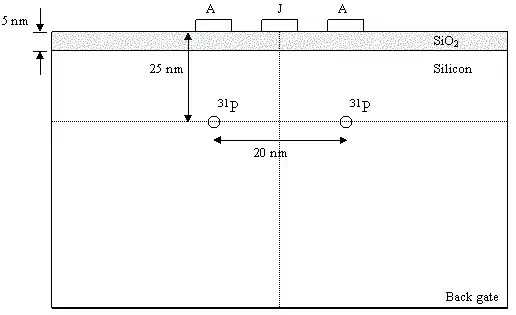
Chaque atome de phosphore possède une grille (ou électrode) de contrôle (grille A) au-dessus et une grille d'échange (grille J) est située entre deux grilles A. Le système est opéré à basse température (~100 mK) et sous champ magnétique (~2 T).
Qubits logiques
L'information quantique est représentée par l'état propre des spins nucléaires. Le spin du noyau atomique de 31P forme un système à deux niveaux (qubit) avec un temps de cohérence potentiellement très élevé (de l'ordre de la centaine de secondes). Un électron piégé sur l'atome de phosphore est utilisé pour contrôler la fréquence de résonance du noyau.
La mesure du qubit est réalisée en transférant l'état quantique du noyau au spin de l'électron, puis en mesurant la capacité entre deux grilles. L'électron possède aussi un bon temps de cohérence (de l'ordre de 2 secondes[5]).
Portes logiques
Les portes logiques à un qubit sont réalisées en utilisant l'électron, contrôlé par la grille A, pour amener le spin du noyau en résonance avec un champ magnétique alternatif. La manipulation du spin se fait alors selon les techniques de la résonance magnétique nucléaire.
Les portes logiques à deux qubits sont réalisées en utilisant la grille J pour déformer la fonction d'onde des électrons de sorte que les deux spins nucléaires soient couplés entre eux à travers les spins électroniques et le couplage hyperfin.
Avantages et inconvénients
L'architecture de Kane comporte plusieurs avantages qui motivent les efforts de recherche encore en 2013 :
- le temps de cohérence est potentiellement très favorable comparativement au temps requis par opération, ce qui permet un faible taux d'erreurs et la correction d'erreur quantique[5] - [4] ;
- elle permet l'informatique quantique universelle[1] ;
- elle peut en principe comporter des millions de qubits (scalable), contrairement à beaucoup d'autres architectures populaires[1] ;
- elle est en principe intégrable avec les composants de base de la microélectronique sur le même substrat[1].
L'architecture possède aussi des inconvénients, notamment :
Références
- B. E. Kane, A silicon-based nuclear spin quantum computer, Nature, vol. 393, no 133 (1998).
- M. Fuechsle, J. A. Miwa, S. Mahapatra, H. Ryu, S. Lee, O. Warschkow, L. C. L. Hollenberg, G. Klimeck et M. Y. Simmons, A single-atom transistor, Nature Nanotechnology, vol. 7, no 242 (2012).
- J. J. Pla, K. Y. Tan, J. P. Dehollain, W. H. Lim, J. J. L. Morton, D. N. Jamieson, A. S. Dzurak et A. Morello, A single-atom electron spin qubit in silicon, Nature, vol. 489, no 541 (2012).
- J. J. Pla, K. Y. Tan, J. P. Dehollain, W. H. Lim, J. J. L. Morton, F. A. Zwanenburg, D. N. Jamieson, A. S. Dzurak et A. Morello, High-fidelity readout and control of a nuclear spin qubit in silicon, Nature, vol. 496, no 334 (2013).
- A. M. Tyryshkin, S. Tojo, J. J. L. Morton, H. Riemann, N. V. Abrosimov, P. Becker, H.-J. Pohl, T. Schenkel, M. L. W. Thewalt, K. M. Itoh et al., Electron spin coherence exceeding seconds in high-purity silicon, Nature Materials, vol. 11, no 143 (2012).