Orbite de transfert

L'orbite de transfert (en jaune) permet de passer de l'orbite basse (en vert) à l'orbite haute (en rouge)

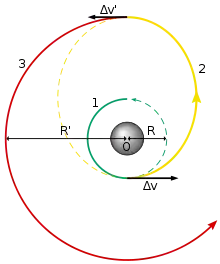
Une trajectoire (aussi appelée transfert, parfois simplement orbite) de Hohmann est une trajectoire qui permet de passer d'une orbite circulaire à une autre orbite circulaire située dans le même plan, en utilisant uniquement deux manœuvres impulsionnelles. En se limitant à deux manœuvres, cette trajectoire est celle consommant le moins d'énergie possible. Avec plus de deux manœuvres par contre, on peut recourir à des transferts dit bi-elliptiques qui se révèlent plus économes en énergie, mais à condition que le rayon de l'orbite d'arrivée excède d'un facteur ~12 celui de l'orbite de départ.

Une orbite de transfert de Hohmann idéale nécessite que les orbites de départ et d'arrivée soient circulaires, dans le même plan orbital et que la trajectoire parcoure 180° de l'orbite de transfert. Dans le monde réel, l'orbite cible peut ne pas être circulaire ni coplanaire et la trajectoire de l'engin spatial peut représenter moins de 180° de l'orbite de transfert ou au contraire plus de 180°. Si la trajectoire parcourt moins de 180° on parle de transfert de Hohmann de type I dans le cas contraire il s'agit d'un transfert de Hohmann de type II[1] - [2].

L'orbite de départ est circulaire de basse altitude, soit, par exemple, ${\displaystyle \scriptstyle {r_{1}=1,15R}}$ (avec R rayon terrestre), de période ${\displaystyle \scriptstyle {T_{1}=T_{0}\left({\frac {r_{1}}{R}}\right)^{3/2}}}$, de vitesse ${\displaystyle \scriptstyle {V_{1}=V_{0}\left({\frac {R}{r_{1}}}\right)^{1/2}}}$, dans laquelle ${\displaystyle \scriptstyle {T_{0}\approx 84\;{\rm {min}}}}$ et ${\displaystyle \scriptstyle {V_{0}\approx \ 8,2\;{\rm {km/s}}}}$.

L'orbite visée est circulaire de haute altitude, soit, par exemple, ${\displaystyle \scriptstyle {r_{2}=6,61R}}$, dont la période ${\displaystyle \scriptstyle {T_{2}=T_{0}\left({\frac {r_{2}}{R}}\right)^{3/2}}}$ et la vitesse ${\displaystyle \scriptstyle {V_{2}=V_{0}\left({\frac {R}{r_{2}}}\right)^{1/2}}}$ sont définies par des formules similaires.

L'orbite de Hohmann est l'ellipse de transfert de périgée ${\displaystyle \scriptstyle {r_{1}}}$ et d'apogée ${\displaystyle \scriptstyle {r_{2}}}$, donc de grand axe ${\displaystyle \scriptstyle {2a=r_{1}+r_{2}\approx 7,76R}}$, et d'excentricité ${\displaystyle \scriptstyle {e={\frac {r_{2}-r_{1}}{r_{2}+r_{1}}}\approx 0,708}}$. Son moment cinétique ${\displaystyle \scriptstyle L}$, son énergie ${\displaystyle \scriptstyle E}$ et sa période ${\displaystyle \scriptstyle T}$ sont donc connues.

Au temps ${\displaystyle \scriptstyle t_{0}}$, le moteur fournit un surcroît de vitesse ${\displaystyle \scriptstyle v}$ au satellite tel que
${\displaystyle m(V_{1}+v)r_{1}=L}$.

Au temps ${\displaystyle \scriptstyle {t_{0}+{\frac {T}{2}}}}$, le satellite parvient à son apogée ${\displaystyle \scriptstyle r_{2}}$ mais avec une vitesse insuffisante. Le moteur fournit un surcroît de vitesse ${\displaystyle v'}$ de sorte que
${\displaystyle L+mv'r_{2}=mV_{2}r_{2}}$.

Il faut donc que le décalage angulaire, au temps ${\displaystyle t_{0}}$, entre la position du satellite ${\displaystyle S_{1}}$ et la position du satellite ${\displaystyle S_{2}}$ soit ${\displaystyle \pi (1-{\frac {T}{T_{2}}})}$, dans le cas d'un rendez-vous.

Le transfert du satellite de ${\displaystyle r_{1}}$ à ${\displaystyle r_{2}}$ entraîne un coût énergétique correspondant aux deux allumages du moteur : surcroît ${\displaystyle v=0,277V_{0}}$, puis ${\displaystyle v'=0,178V_{0}}$.

• Orbite
• Orbite de transfert géostationnaire
• Effet Oberth
• Orbite d'attente
• Orbite de rebut
• Orbitographie

• Une simulation animée du changement d'orbite, avec pilotage manuel ou automatique
• Illustration du voyage vers la planète Mars
• Droit français : arrêté du 20 février 1995 relatif à la terminologie des sciences et techniques spatiales.