Numération maya
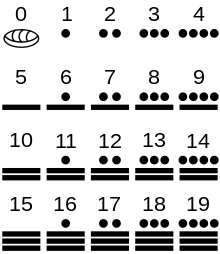
La numération maya est une numération de base vingt pratiquée dans la civilisation mésoaméricaine maya. Durant la période classique et post-classique, du IIIe au XIIIe siècle, on a la trace d'une numération de position écrite savante, à sous-base quinaire, vigésimale à une irrégularité près. Les chiffres constitutifs de cette numération, de 1 à 19, possèdent plusieurs écritures possibles, ou bien sous forme de glyphes céphalomorphes, ou à l'aide d'un système répétitivo-additif de traits valant 5 et de points valant 1.
Les Mayas distinguaient l'aspect cardinal de l'aspect ordinal du nombre, et ne confondaient pas, par exemple, une durée avec une date.
Ils ont inventé des signes différents, attestés dès le IVe siècle, pour noter les deux aspects, ordinal et cardinal, du nombre zéro.
Leur énonciation des nombres a la particularité, rare dans la numération orale, de procéder par protraction en se référant non à la vingtaine inférieure mais à la nouvelle vingtaine commencée.
Traces dans l'histoire
_-_Guatemala-0572.jpg.webp)
Les mayanistes ne disposent que de rares documents pour étudier le système de numération écrite maya. Tous les codex ont été brûlés lors de la conquête espagnole à l'exception de trois d'entre eux : le codex de Dresde, celui de Paris et celui de Madrid[2] . Il est donc pour l'instant impossible d'avoir une bonne idée de leur système métrologique (volume, surface, longueurs, quantité de graines, quantité de bétail...). À l'exception de quelques quantités (offrandes, nombre de prisonniers) les seules utilisations attestées concernent la mesure du temps[3].
Sur ce cas particulier, les traces de numération sont nombreuses : dans les cités, sur les stèles, les frontons de portes, les Mayas ont gravé l’histoire des cités et des rois ou la marche du Soleil et des planètes visibles à l’œil nu. De telles traces sur les monuments mayas sont relevées entre 290 après J.C. pour la plus ancienne jusqu'à 909 après J.C. pour la plus récente[4].
Sur les Codices, ils ont noté la marche des planètes visibles, ont calculé, à l'aide de tables de multiples, les occurrences de conjonctions entre leur divers calendriers dans un but numérologique et astrologique, pour déterminer les périodes fastes et néfastes à toute entreprise[5].
Dans les cités mayas, les gens utilisaient la numération parlée de leur langue (chol, yucatèque, etc.) et les scribes disposaient de plusieurs numérations écrites ainsi que d'un système d'unités de temps. Ces systèmes étaient tous de caractère vigésimal.
Comptage du temps

Pour écrire les petits nombres, par exemple la durée d'une lunaison (c'est-à-dire les entiers 29 ou 30) ou les petits déplacements (dans l'almanach divinatoire de 260 jours), les Mayas disposaient d'une numération de type additif utilisant trois signes pour 1, 5 et 20 ; dans cette écriture : '20,9' s'interprète 20 + 9. On trouve ainsi le nombre 62 écrit à l'aide de 3 signes « 20 » complétés de 2 points dans le codex de Madrid[6].
Les mayas utilisaient quatre systèmes principaux de comptage du temps. L'un, le calendrier Tzolk'in, fait référence à une année liturgique de 260 jours associant 20 noms de jours à 13 numéros de jours. Pour un tel calendrier, seuls 13 nombres sont nécessaires. Un autre, le calendrier Haab fait référence à l'année « vague » de 365 jours découpée en 18 mois de 20 jours et un mauvais mois de 5 jours. Utilisant un système de numérotation des jours dans le mois de 0 à 19, il ne leur était pas nécessaire de développer une numération au delà de 20. La donnée d'une date sous les deux formes Tzolk'in et Haab, permettait de préciser la position d'un événement sur une période de 18 980 jours (ou 52 années vagues), le calendar round[7].
Seul le dernier calendrier, utilisant le compte long, comptage du nombre de jours écoulés depuis la naissance d'un nouveau cycle du monde, naissance évaluée en 3114 avant J.C.[8], nécessitait de mettre en place un système de numération solide. Ce système consiste à compter le temps écoulés à l'aide d'une « année » (ou tun) de 360 jours (ou 360 kin), année découpée en 18 mois (ou uinal) de 20 jours. Un groupe de 20 tun porte le nom de katun, un groupe de 400 tun ou 20 katun porte le nom de baktun, s'ensuivent d'autres noms régulièrement construits : pictun pour 20 baktun, calabtun pour 20 pictun, etc[9].
Sur la plupart des dates en compte long figurant sur les monuments, c'est un système d'écriture avec unités qui est donnée, où la date est précisée en 5 glyphes en commençant par les poids forts (baktun. katun. tun. uinal. kin)[10]. Ainsi la plaque de Leyde indique une date de 8 baktun, 14 katun, 3 tun, 1 uinal, 12 kin soit 1 253 912 j écoulés depuis le point de départ du calendrier et permet de dater la plaque de l'an 320 de l'ère chrétienne[11]. Les distances, ou intervalles entre deux dates, quant à elles, sont souvent présentées avec leurs unités mais en commençant par les poids faibles (kin, uinal, tun, etc.)[12]. Malgré l'apparition d'un zéro de position, cette habitude de préciser les unités persiste sur les monuments tandis que la numération de position sans unité est majoritaire dans les codices[13].
La présence avérée d'un cycle de 13 baktun dans la cosmologie maya a pu faire croire que les dates en compte long ne devaient pas dépasser 13 baktun (et donc 5 chiffres). Cette hypothèse (dite hypothèse courte) est réfutée par l'existence d'intervalles de temps gravés en compte long et dépassant 13 baktuns[14] laissant soupçonner un système ouvert du comptage du temps.
Cette pratique du compte long et de l'écriture positionnelle associée n'est pas l'apanage de la civilisation maya et l'on trouve des écritures de ce type sur le site olmèque de Tres Zapotes qui daterait de 32 avant J.C[15], si les Olmèques ont bien pris le même point de départ, ou bien sur la Stèle n° 1 de La Mojarra datée de 156 après J.C.
Numération de position
_(20468176849).jpg.webp)
Cette sorte de numération très présente dans les codices est toujours utilisée dans le cadre du compte long et présente donc une irrégularité due au fait que dans un tun il n'y a que 18 uinal et non 20[3].
L'écriture d'un nombre se fait par empilement de chiffres. Chaque étage correspond à un poids 20 fois supérieur au poids de l'étage inférieur, à l'exception du passage du 2e au 3e étage où la multiplication n'est que de 18. Ainsi la valeur de l'étage le plus bas est multipliée par 1, du second étage par 20, du troisième étage par 20 × 18 = 360, du quatrième étage par 400 × 18 = 7200 et ainsi de suite, la valeur du ne étage (pour n > 2) étant multipliée par 20n-2 × 18. Par exemple :
|
Cette notation positionnelle est utilisée autant pour donner des dates que pour les intervalles de temps ou distance entre dates. Dans ce cadre, les Mayas distinguaient les distances positives vers le futur et les distances négatives, vers le passé qu'ils identifiaient à l'aide d'un symbole spécial mis sur le chiffre des unités (une sorte d'anneau)[18].
À cause de l'irrégularité présente entre le deuxième chiffre et le troisième, la multiplication par la base ne peut pas se réduire à un simple décalage des chiffres vers le haut. Cette absence de zéro opérateur, présent dans la numération sexagésimale savante mésopotamienne, est, pour Geneviève Guitel[19], une limitation de la numération maya, alors que Cauty et Hoppan font remarquer que cette irrégularité n'est pas un réel obstacle. En effet, si un nombre s'écrit, en numération maya , le multiplier par 1.0 conduit bien à décaler tous les chiffres sauf les premiers: Si le nombre entre parenthèses est plus petit que 18, on obtient directement l'écriture du résultat. Sinon, un jeu sur les retenues, permet de trouver rapidement la bonne écriture[20].
Chiffres céphalomorphes
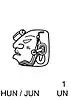
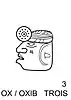
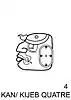
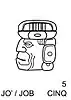
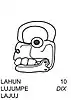
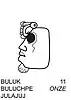
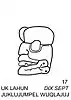
Les scribes mayas disposaient, outre du système des chiffres point/barre ci-dessus, de nombreuses formes graphiques pour représenter les vingt chiffres nécessaires à l'écriture de leurs nombres (le plus souvent des durées) ou des unités de leur système d'unités de temps (les glyphes de période: kin, uinal, tun, katun, baktun, etc.). Le plus célèbre système est certainement celui des chiffres céphalomorphes (chaque chiffre, de 0 à 19, est représenté par un glyphe ayant la forme d'une tête). Chaque chiffre correspond à un dieu identifiable le plus souvent à ses attributs. On y retrouve des dieux célestes comme certains de l'Inframonde reconnaissables à la présence du maxillaire inférieur. Sur les vignettes apparaissent les nombres correspondant en 3 langues Maya : Yucatèque, puis Chol (langue de la plupart des cités classiques du Peten) puis K'iche'.
La construction des chiffres de 13 à 19, se rapproche de leur énonciation : il s'agit d'ajouter 10 (lahun - représentée par une tête de mort) aux chiffres 3, 4, ... ou 9. Les têtes représentants 13, 14, ..., 19 reprennent donc les têtes 3, 4, ..., 9 avec le simple ajout d'un maxillaire inférieur décharné[21].
Deux zéros mayas
Les scribes mayas utilisaient une numération vigésimale (à base vingt) et ils disposèrent de deux zéros distincts, marqués par des glyphes différents[22]. De manière générale, ils distinguaient toujours soigneusement les durées (de nature cardinale) et les dates (de nature ordinale), par exemple dans les almanachs divinatoires, en écrivant les premières en noir et les secondes en rouge. Ils ont donc créé deux types de zéro : un zéro ordinal et un zéro cardinal.
Zéro ordinal
Le zéro ordinal servait à noter le premier jour des 18 mois de vingt jours ou de la période complémentaire de cinq jours qui constituent l'année solaire (le ha'ab de 365 jours). Par exemple, le premier de l'an était un 0 Pop.
Ce zéro ordinal est plus ancien que le zéro cardinal car attesté pour la première fois par une pendeloque de jade (connue sous le nom de plaque de Leyde), et il date du 17 septembre 320 (apr. J.-C.)[23]. Sur cette pendeloque, le même glyphe apparaît aussi dans un contexte « littéraire » où il note le verbe CHUM désignant l'action de monter sur le trône, l'intronisation du roi dont la figure apparaît au recto de la plaque. Le premier jour de chaque mois (jour 0) est considéré comme le jour d'installation dans le mois, ce qui explique ce glyphe d'installation[24]. Le second jour du mois est donc à comprendre comme le 1e jour après l'installation dans le mois.
Zéro cardinal
Le zéro cardinal, est un zéro de position, comme celui de la numération décimale ou de toute autre numération de position. Par exemple : 9.9.16.0.0. (codex de Dresde p. 24) note la durée 9-baktun 9-katun 16-tun 0-uinal 0-kin, c'est-à-dire la durée de 9 x 400 tun (année de compte de 360 jours) + 9 x 20 tun + 16 tun + 0 uinal (mois de 20 jours) + 0 kin (jour).
Un chiffre zéro cardinal est attesté pour la première fois par les stèles 18 et 19 de Uaxactun (Peten, Guatemala) datées du 3 février 357 où ses trois occurrences en position finale ont la forme d'une fleur à 4 pétales mais dont le dernier pétale est masqué par le nom de la période[25]. Une autre forme de ce zéro de position, céphalomorphe, est celle de la main de l'accomplissement, ou celle du miroir d'obsidienne. Dans les codex du Postclassique, le zéro de position a la forme d'un couteau (notamment de couteau sacrificiel) et parfois la forme d'un coquillage[26].
La plus vieille attestation d'un zéro purement de position, sans indication de période est attesté sur une stèle de Pestac dans l'écriture 9.11.12.9.0 correspondant à l'année 665 après J.C.[27].
Numération parlée (yucatèque, données de Beltran, XVIIIe siècle)
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ces formes font apparaître la spécificité des numérations mayas parlées précolombiennes, à savoir que les Mayas disposaient d'une opération que nous ne connaissons pas dans notre arithmétique. Une opération qui donne le résultat 45 quand on la fait porter sur les arguments 5 (Ho) et 60 (oxkal) ). Le linguiste Claude Hagège a proposé d'appeler cette opération « opération de protraction ». Le constituant «tu» («tuy» devant voyelle) est la contraction du locatif «ti» signifiant «vers, en » et de l'indice personnel de 3e personne «u-», lequel sert à dériver l'ordinal à partir du cardinal (comme notre suffixe -ième qui fait passer de 3 à 3e)[30].
Selon André Cauty, la numération parlée yucatèque est d'un type spécial que l'on peut dire ordinal en vision d'antériorité rétrograde[30]. En effet, si l'expression de 45 (Ho tuy oxkal) dit quelque chose comme «cinq vers le 3e vingt», sa valeur numérique 45 ne peut être obtenue qu'en revenant au 2e vingt.
Le relateur «tu> peut être sous-entendu comme dans 30 (lahucakal). Dans les composés de la deuxième vingtaine (de 21 à 39), les yucatèques ne précisent généralement pas le coefficient du «vingt» dont il est question (et qui ne peut être que le premier valant la peine d'être cité, c'est-à-dire 2) comme dans l'expression «hun tu kal» de 21[30].
La protraction concerne aussi les nœuds supérieurs de la numération comme 900 s'écrivant «ho tuy ox bak», expression dans laquelle «kal» est sous-entendu et qui peut se traduire par «cinq (vingtaines) vers la 3e quatrecentaine»[30].
Les Mayas transcrivaient parfois par écrit les sons de l'expression parlée du petit nombre; les exemples sont rares (trois dans le codex de Dresde) mais ils sont précieux parce qu'on a alors une trace écrite de l'opération de protraction avec présence du syllabogramme «tu» qui fournit par exemple la valeur 35 à l'aide de trois composantes : le chiffre 15, la syllabe «tu» et le graphe «uinal» (le coefficient 2 étant là aussi élidé)[30].
La notation protractive est aussi attestée sur les monuments pour noter l'âge de la Lune. C'est le compte des jours depuis la nouvelle Lune qui s'exprime par un signe composé lorsqu'il est compris entre 21 et 30. Dans ce cas, le scribe n'écrivait pas le signe «tu» de l'opération de protraction et juxtaposait les deux arguments. L'âge 29 par exemple s'écrivait «9,20», dans l'ordre croissant. Cet ordre distingue la notion d'âge de la lune de celle de durée d'une lunaison et oppose la protraction à l'addition : par exemple, la lunaison de vingt-neuf jours, elle, était notée «20,9» dans l'ordre décroissant des arguments[31].
Notes et références
- Pour une traduction complète, lire (de) John F. Harris, John Ferguson Harris et Stephen K. Stearns, Understanding Maya Inscriptions : A Hieroglyph Handbook, UPenn Museum of Archaeology, , pages 154 et suivantes ou The Stelae of Quirigua | Uncovered History
- Ifrah 1981.
- Cauty et Hoppan 2007, p. 5.
- T. Jones et Selin, p. C-14.
- T. Jones et Selin, p. 465.
- Cauty et Hoppan 2007, p. 15.
- Cauty et Hoppan 2007, p. 6.
- T. Jones et Selin, p. C-13.
- Ifrah 1981, p. 439.
- Cauty et Hoppan 2007, p. 17.
- Ifrah 1981, p. 443.
- T. Jones et Selin, p. C-18.
- Cauty et Hoppan 2007, p. 9.
- Cauty et Hoppan 2007, p. 19.
- Malmström 2008, p. 1235.
- Ifrah 1981, p. 452.
- Cauty 1998, p. 10.
- Closs 2008, p. 1408.
- Geneviève Guitel, Histoire comparée des numérations écrites, Flammarion,
- Cauty Hoppan.
- Cauty et Hoppan 2007, p. 2.
- [PDF] Red Latinoamericana de Etnomatemática: Les deux zéros mayas
- André Cauty, « Zéro : un agent double maya », p=1
- Ifrah 1981, p. 435.
- Cauty Zéro, p. 2.
- Cauty Zéro, p. 4.
- Closs et Selin, p. 1408.
- (es) Pedro Beltrán de Santa Rosa, Arte del idioma maya reducido a sucintas reglas y semilexicon yucateco, (lire en ligne), pp 195 et suivantes
- Beltran (Beltran 1742, p. 201) signale que les indiens d'origine utilisaient «pic» pour 8 000 mais qu'au moment de sa transcription, l'usage était plutôt de lui donner la valeur 1000.
- Cauty et Hoppan 2007, p. 3.
- Cauty et Hoppan 2007, p. 4.
Bibliographie
- (en) Helaine Selin (dir.), Encyclopædia of the History of Science, Technology, and Medecine in Non-Western Cultures, Springer Verlag, ;
- Martha J. Macri Jones, « Astronomy in Mesoamerica », dans Encyclopædia of the History of Science, Technology, and Medecine in Non-Western Cultures;
- Tom Jones, « Calendars in Mesoamerica », dans Encyclopædia of the History of Science, Technology, and Medecine in Non-Western Cultures;
- Keith Jordan, « Cosmology in Mesoamerica », dans Encyclopædia of the History of Science, Technology, and Medecine in Non-Western Cultures;
- Vincent H. Malmström, « Long count », dans Encyclopædia of the History of Science, Technology, and Medecine in Non-Western Cultures;
- Michael P. Closs, « Mathematics : Maya Mathematics », dans Encyclopædia of the History of Science, Technology, and Medecine in Non-Western Cultures.
- Georges Ifrah, Histoire universelle des chiffres, Paris, Seghers, , 567 p. (ISBN 2-221-50205-1);
- André Cauty et Jean-Michel Hoppan, « Les Écritures mayas du Nombre », ;
- André Cauty, « Lire et faire parler un texte : par qui et comment les pages 24 à 29 du «Codex de Dresde» peuvent-elles être traduites », Amerindia, no 23, (lire en ligne).
Voir aussi
Articles connexes
Liens externes
- (en) Reading Maya Hieroglyphs - Apprentissage interactif en Shockwave
- (en) Maya Mathematics - Conversion en ligne depuis le système décimal à la numération maya.
- IAM - Intelligence Arithmétique Maya d'André Cauty : blog site
- « Les Écritures mayas du nombre »
- « Numération et action. Le cas des numérations mayas »