Nombre composé
Un nombre composé est un entier naturel différent de 0 qui possède un diviseur positif autre que 1 ou lui-même. Par définition, chaque entier plus grand que 1 est donc soit un nombre premier, soit un nombre composé, et les nombres 0 et 1 ne sont ni premiers ni composés.
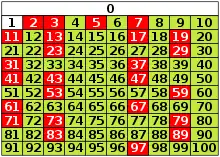
Autre définition : un nombre composé est le produit d'au moins deux nombres premiers (qu'ils soient distincts ou identiques).
Par exemple, l'entier 14 est un nombre composé parce qu'il a les nombres 1, 2, 7 et 14 pour diviseurs (quatre diviseurs).
Tous les entiers naturels pairs, hormis zéro et 2, sont composés. La méthode permettant de lister tous les entiers naturels impairs composés est appelée crible de Sundaram.
Propriétés
- Tous les nombres pairs plus grands que 2 sont composés.
- Le plus petit nombre composé est 4.
- Chaque nombre composé peut être écrit comme un produit de plusieurs nombres premiers (non nécessairement distincts).
- Un nombre est un carré parfait si et seulement si son nombre de diviseurs est impair.
- pour tout nombre composé n > 5.
- La moyenne arithmétique de deux nombres premiers consécutifs impairs (parfois appelée nombre interpremier), comme 6 = 5 + 72 ou 9 = 7 + 112, est toujours un nombre composé.
Densité asymptotique
La raréfaction des nombres premiers montre que la proportion des nombres composés entre 1 et n tend vers 1 lorsque n tend vers +∞, autrement dit qu’ils sont de densité asymptotique[1] égale à 1.
Généralisation aux entiers relatifs
Un entier relatif est dit composé si sa valeur absolue est un entier naturel composé. Par exemple : -4 est composé.
Sortes de nombres composés
Une manière de classer les nombres composés consiste à compter le nombre de facteurs premiers. Un nombre composé avec deux facteurs premiers est un nombre semi-premier ou un nombre 2-presque premier (les facteurs n'ont pas besoin d'être distincts, par conséquent, les carrés de nombres premiers sont inclus). Un nombre composé avec trois facteurs premiers distincts est un nombre sphénique. Dans quelques applications, il est nécessaire de différencier les nombres composés d'un nombre impair 2x + 1 de facteurs premiers distincts de ceux composés d'un nombre pair 2x de facteurs premiers distincts. Pour ce dernier cas
(où μ est la fonction de Möbius), tandis que pour le cas précédent
Par exemple, si x = 0 : μ(1) = 1 et pour tout nombre premier p, μ(p) = –1. Pour un nombre n avec un ou plus de nombres premiers répétés, μ(n) = 0.
Une autre manière de les classer consiste à compter le nombre de diviseurs. Tous les nombres composés ont au moins trois diviseurs. Dans le cas du carré d'un nombre premier p, ces diviseurs sont 1, p et p2. Un nombre n qui possède plus de diviseurs qu'un x < n quelconque est un nombre hautement composé (bien que les deux premiers de ces nombres soient 1 et 2).
Premiers nombres composés
Les vingt premiers nombres composés sont (suite A002808 de l'OEIS)
4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32.
Le crible de Sundaram donne une méthode simple pour générer tous les nombres composés impairs.
Notes et références
- En l’absence d’une loi de probabilité sur N pour laquelle la probabilité d’obtenir un nombre multiple de k vaille 1/k, on ne peut raisonner en termes de probabilité d’obtenir un nombre composé.


