Modèle d'eau
En chimie numérique, les modèles d'eau classiques sont utilisés pour la simulation de l'eau et des solutions aqueuses (avec ce qu'on appelle un solvant explicite, par opposition aux modèles à solvants implicites). Ces modèles utilisent généralement les approximations de la mécanique moléculaire. De nombreux et différents modèles ont été proposés ; ils peuvent être classés en fonction du nombre de points employés pour définir le modèle (atomes plus sites spécifiques), de la rigidité ou de la flexibilité de la structure, ou encore de la prise en compte des effets de polarisation.
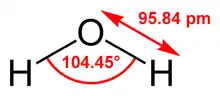
Les modèles simples : présentation
Les modèles d'eau les plus simples considèrent la molécule d'eau comme rigide et reposent sur les interactions non-liantes. L'interaction électrostatique est modélisée en utilisant la loi de Coulomb et les forces de dispersion et de répulsion en utilisant un potentiel de Lennard-Jones.
Les sites chargés peuvent se situer sur les atomes ou sur des sites spécifiques (comme les paires non-liées). Le terme de Lennard-Jones est typiquement appliqué de manière restreinte aux atomes d'oxygène.
La figure ci-dessous montre la forme générale des modèles d'eau de 3 à 6 sites. Les paramètres géométriques exactes (la longueur de la liaison OH et la valeur de l'angle HOH) sont variables selon le modèle.
Modèles à trois sites
Le modèle le plus simple comprend trois sites d'interactions, correspondant aux trois atomes de la molécule d'eau. Chaque atome se voit assigner une charge ponctuelle, et l'atome d'oxygène se voit aussi doté de paramètres de Lennard-Jones. Les modèles à 3 sites sont très utilisés pour les simulations de dynamique moléculaire en raison de leur simplicité et de leur efficacité dans les calculs. La plupart des modèles utilisent une géométrie rigide reproduisant la géométrie d'une molécule d'eau. Une des exceptions est le modèle SPC, qui suppose un angle tétraédrique idéal (soit 109,47° pour l'angle HOH) au lieu de la valeur observée de 104,5°.
Le tableau ci-dessous liste les paramètres de quelques modèles à 3 sites.
| TIPS[1] | SPC[2] | TIP3P[3] | SPC/E[4] | |
|---|---|---|---|---|
| r(OH), Å | 0,9572 | 1,0 | 0,9572 | 1,0 |
| HOH, deg | 104,52 | 109,47 | 104,52 | 109,47 |
| A × 10−3, kcal Å12/mol | 580,0 | 629,4 | 582,0 | 629,4 |
| B, kcal Å6/mol | 525,0 | 625,5 | 595,0 | 625,5 |
| q(O) | −0,80 | −0,82 | −0,834 | −0,8476 |
| q(H) | +0,40 | +0,41 | +0,417 | +0,4238 |
Le modèle SPC/E ajoute une correction de polarisation moyenne à la fonction d'énergie potentielle :
dans laquelle μ est la valeur du dipôle de la molécule d'eau effectivement polarisée (2,35 D pour le modèle SPC/E), μ0 est la valeur du dipôle d'une molécule d'eau isolée (1,85 D d'après l'expérience), et αi est une constante de polarisibilité isotrope, de valeur 1,608 × 10−40 F.m. Les charges du modèle étant constantes, cette correction n'entraîne qu'un ajout de 1,25 kcal/mol (5,22 kJ/mol) à l'énergie totale. Le modèle SPC/E donne une meilleure densité et une meilleure constante de diffusion que le modèle SPC.
Autres modèles :
- Fergunson (SPC flexible)
- CVFF (flexible)
Modèles à 4 sites
Les modèles à 4 sites situent la charge négative sur un pseudo-atome (noté M dans la figure) placé près de l'oxygène le long de la bissectrice de l'angle HOH. Cette disposition améliore la distribution de la charge électrostatique autour de la molécule d'eau. Le premier modèle à avoir utilisé cette approche fut le modèle de Bernal-Fowler publié en 1933, qui fut d'ailleurs aussi le premier modèle d'eau. Cependant, ce modèle ne reproduit pas correctement les propriétés massiques de l'eau, comme par exemple la densité et l'énergie de vaporisation, et il n'est donc que d'intérêt historique. C'est une conséquence directe de la méthode de paramétrisation choisie; des modèles plus récents, utilisant les techniques de calculs informatiques disponibles depuis, ont été paramétrés en utilisant des simulations de type Monte Carlo ou des simulations de dynamique moléculaire et ces paramètres ont été ajustés jusqu'à obtention d'une bonne reproduction des propriétés massiques.
Le modèle TIP4P, publié initialement en 1983, est très largement implémenté dans les codes de chimie numérique et est parfois utilisé pour les simulations de systèmes biomoléculaires. Il y a eu des reparamétrisations importantes du modèle TIP4P pour des usages spécifiques : le modèle TIP4P-Ew, pour des utilisations avec des méthodes de sommation d'Ewald; le TIP4P/Ice, pour les simulations d'eau solide (glace); et TIP4P/2005, une paramétrisation générale pour la simulation complète du diagramme de phases de l'eau.
| BF[5] | TIPS2[6] | TIP4P[3] | TIP4P-Ew[7] | TIP4P/Ice[8] | TIP4P/2005[9] | |
|---|---|---|---|---|---|---|
| r(OH), Å | 0,96 | 0,9572 | 0,9572 | 0,9572 | 0,9572 | 0,9572 |
| HOH, deg | 105,7 | 104,52 | 104,52 | 104,52 | 104,52 | 104,52 |
| r(OM), Å | 0,15 | 0,15 | 0,15 | 0,125 | 0,1577 | 0,1546 |
| A × 10−3, kcal Å12/mol | 560,4 | 695,0 | 600,0 | 656,1 | 857,9 | 731,3 |
| B, kcal Å6/mol | 837,0 | 600,0 | 610,0 | 653,5 | 850,5 | 736,0 |
| q(M) | −0,98 | −1,07 | −1,04 | −1,04844 | −1,1794 | −1,1128 |
| q(H) | +0,49 | +0,535 | +0,52 | +0,52422 | +0,5897 | +0,5564 |
Autres :
- TIP4PF (flexible)
Modèles à 5 sites
Les modèles à 5 sites situent la charge négative sur des atomes fictifs (notés L) représentant les doublets non liants de l'atome d'oxygène. Un des modèles les plus anciens fut le modèle BNS de Ben-Naim et Stillinger, proposé en 1971, qui fut rapidement suivi du modèle ST2 de Stillinger et Rahman en 1974. En raison principalement de leur coût de calcul important, les modèles à cinq sites ne furent que peu développés jusqu'aux années 2000, lorsque le modèle TIP5P de Mahoney et Jorgensen fut publié. Lorsqu'on le compare aux modèles plus anciens, le modèle TIP5P procure des améliorations dans la géométrie pour les dimères d'eau, une structure plus tétrahédrique qui reproduit mieux les fonctions de distributions radiales obtenues à partir de la diffraction de neutrons, et la température de la densité maximale de l'eau. Le modèle TIP5P-E est une reparamétrisation du modèle TIP5P pour l'utilisation de sommes d'Ewald.
| BNS[10] | ST2[10] | TIP5P[11] | TIP5P-E[12] | |
|---|---|---|---|---|
| r(OH), Å | 1,0 | 1,0 | 0,9572 | 0,9572 |
| HOH, deg | 109,47 | 109,47 | 104,52 | 104,52 |
| r(OL), Å | 1,0 | 0,8 | 0,70 | 0,70 |
| LOL, deg | 109,47 | 109,47 | 109,47 | 109,47 |
| A × 10−3, kcal Å12/mol | 77,4 | 238,7 | 544,5 | 590,3 |
| B, kcal Å6/mol | 153,8 | 268,9 | 554,3 | 628,2 |
| q(L) | −0,19562 | −0,2357 | −0,241 | −0,241 |
| q(H) | +0,19562 | +0,2357 | +0,241 | +0,241 |
| RL, Å | 2,0379 | 2,0160 | ||
| RU, Å | 3,1877 | 3,1287 |
On notera cependant que les modèles BNS et ST2 n'utilisent pas directement la loi de Coulomb pour les termes électrostatiques, mais une version modifiée qui est atténuée pour de faibles distances en étant multipliées par une fonction de permutation S(r) :
Ainsi, les paramètres RL et RU s'appliquent seulement aux modèles BNS et ST2.
Modèles à 6 sites
On notera l'existence d'au moins un modèle à 6 sites développé par Nada et van der Eerden[13] qui combine tous les sites des modèles à 4 et 5 sites. Ce modèle reproduit de meilleure manière la structure et les mélanges de glace (il existe en effet plusieurs types de phases pour l'eau solide) que les autres modèles.
Autres modèles
- Le modèle MB. Ce modèle plus abstrait - ressemblant au logo de la marque Mercedes-Benz - reproduit certaines propriétés de l'eau dans des systèmes bidimensionnels. Il n'est pas utilisé comme tel pour des simulations de systèmes « réels » donc tridimensionnels, mais il reste utile pour des études qualitatives ainsi que pour des propos éducatifs[14].
- Des modèles cœur-couche. Des modèles de ce type à un et deux sites ont aussi été développés[15].
Coût numérique
Le coût numérique des simulations d'eau s'accroît avec le nombre de sites d'interaction du modèle utilisé. Le temps processeur est approximativement proportionnel au nombre de distances interatomiques qui doivent être calculées. Pour un modèle à 3 sites, 9 distances sont nécessaires pour chaque paire de molécules d'eau (de chaque atome de l'une à chaque atome de l'autre). Pour un modèle à 4 sites, 10 distances sont requises (chaque site chargé avec chaque site chargé, ainsi que l'interaction O-O). Pour un modèle à 5 sites, 17 (4 × 4 + 1). enfin, pour un modèle `a 6 sites, 26 distances sont nécessaires (5 × 5 + 1).
Lorsque des modèles d'eau rigides sont utilisés dans une dynamique moléculaire, il existe un coût supplémentaire associé à la conservation de la contrainte structurale, correspondant à l'utilisation d'algorithmes de contrainte.
Voir aussi
Références
- Jorgensen, W. L. Quantum and statistical mechanical studies of liquids. 10. Transferable intermolecular potential functions for water, alcohols, and ethers. Application to liquid water. J. Am. Chem. Soc. 1981, 103, 335-340.
- H.J.C. Berendsen, J.P.M. Postma, W.F. van Gunsteren, and J. Hermans, In Intermolecular Forces, edited by B. Pullman (Reidel, Dordrecht, 1981), p. 331.
- Jorgensen, W. L.; Chandrasekhar, J.; Madura, J.; Impey, R. W.; Klein, M. L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys 1983, 79, 926-935. DOI 10.1063/1.445869
- H. J. C. Berendsen, J. R. Grigera, and T. P. Straatsma. The Missing Term in Effective Pair Potentials. J. Phys. Chem 1987, 91, 6269-6271. DOI 10.1021/j100308a038
- Bernal, J. D.; Fowler, R.H. J. Chem. Phys. 1933, 1, 515. DOI 10.1063/1.1749327
- Jorgensen, W. L. Revised TIPS for simulations of liquid water and aqueous solutions. J. Chem. Phys 1982, 77, 4156-4163. DOI 10.1063/1.444325
- H. W. Horn, W. C. Swope, J. W. Pitera, J. D. Madura, T. J. Dick, G. L. Hura, and T. Head-Gordon. Development of an improved four-site water model for biomolecular simulations: TIP4P-Ew. J. Chem. Phys. 2004, 120, 9665-9678. DOI 10.1063/1.1683075
- J. L. F. Abascal, E. Sanz, R. García Fernández, and C. Vega. A potential model for the study of ices and amorphous water: TIP4P/Ice. J. Chem. Phys. 2005, 122, 234511. DOI 10.1063/1.1931662
- J. L. F. Abascal and C. Vega. A general purpose model for the condensed phases of water: TIP4P/2005. J. Chem. Phys. 2005, 123, 234505. DOI 10.1063/1.2121687
- F.H. Stillinger, A. Rahman, Improved simulation of liquid water by molecular dynamics. J. Chem. Phys. 1974, 60, 1545-1557. DOI 10.1063/1.1681229
- Mahoney, M. W.; Jorgensen, W. L. A five-site model liquid water and the reproduction of the density anomaly by rigid, non-polarizable models. J. Chem. Phys. 2000, 112, 8910-8922. DOI 10.1063/1.481505
- Rick, S. W. A reoptimization of the five-site water potential (TIP5P) for use with Ewald sums. J. Chem. Phys. 2004, 120, 6085-6093. DOI 10.1063/1.1652434
- H. Nada, J.P.J.M. van der Eerden, J. Chem. Phys. 2003, 118, 7401. DOI 10.1063/1.1562610
- K. A. T. Silverstein, A. D. J. Haymet, and K. A. Dill. A Simple Model of Water and the Hydrophobic Effect. J. Am. Chem. Soc. 1998, 120, 3166-3175. DOI 10.1021/ja973029k
- S. Izvekov, G. A. Voth. Multiscale coarse graining of liquid-state systems J. Chem. Phys. 2005, 123, 134105. DOI 10.1063/1.2038787
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Water model » (voir la liste des auteurs).



