Mathématiques incas

Extension maximale de l'empire inca et de ses quatre régions principales

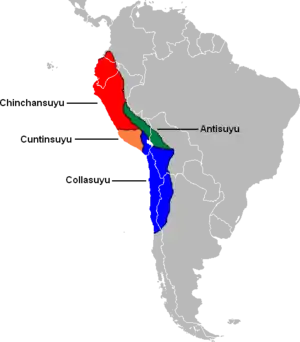
Les géographies variées des Andes, du bassin amazonien, de la côte du Pacifique et des déserts environnants donnent à l'empire inca une géologie et un climat très variés et instables, en plus des inondations, sécheresses et tremblements de terre périodiques. Ces aspects indiquent un besoin de connaissances mathématiques : le génie agricole et le génie civil sont essentiels à la survie, par exemple pour le contrôle de l'irrigation et la construction de ponts[4].

De plus, comme pour toute autre groupe humain, la connaissance et la prédiction des saisons et du climat se développement de pair avec les mathématiques et l'astronomie[4].

Comme mentionné précédemment, l'empire inca était formé de plusieurs groupes culturels, chacun avec ses propres pratiques et connaissances mathématiques. Lors de leur absorption dans l'empire, ces connaissances ont presque certainement été aussi assimilées[5].

Les Moches, du nord du Pérou, ont pu apporter des connaissances reliées à l'agriculture avec l'irrigation par des rivières. Les Huaris pratiquaient l'irrigation en terrasses et leur art était en grande partie basé sur des mathématiques. Les Aymaras pratiquaient aussi ce type d'agriculture ainsi que de la domestication de lamas et d'alpacas. Un autre groupe est les Nazcas, du sud du Pérou, dont les géoglyphes révèlent une compréhension de la géométrie et de l'astronomie[5].

Un exemple concret de contribution de groupes culturels distincts, est le quipu, qui était connu des Huaris et Aymaras avant la prise d'ampleur de l'empire inca[5]. Par ailleurs tous les groupes de l'empire inca, même s'ils pouvaient jouir d'une certaine indépendance, étaient taxés. Les quipus étaient donc essentiels aux archives et à l'administration de l'État, dans ce contexte culturellement varié[6].

Le quipu péruvien VA 42527 (Museum für Völkerkunde, Berlin), déjà étudié par Gary Urton, comporte une division en quatre quadrants très particulière. En associant l’analyse statistique des données à une étude de type expérimentale de ce quipu, de façon curieuse, Alberto Sáez-Rodríguez[7] ouvre de nouvelles pistes de recherche dans l’étude des quipus. Dans son article scientifique, Alberto Sáez-Rodríguez prouve l'existence d'une carte stellaire en deux dimensions, correspondant aux coordonnées X, Y des 6 étoiles les plus brillantes de l'amas ouvert des Pléiades (M45). L’enjeu de ce travail est de démontrer que les Incas connaissaient bien un système de coordonnées rectangulaires 200 ans avant René Descartes.

On connait surtout les quipus pour l'utilité qu'en avait l'administration inca. Ceux-ci s'en servaient pour toute la gestion économique et sociale de l'empire. Les quipucamayocs (« maîtres du Quipu »), présents au nombre de trois au minimum dans chaque communauté recensaient toutes les données démographiques et économiques du lieu. Ces données renvoyées vers les centres administratifs de l'empire permettaient aux Incas de contrôler la prospérité des communautés. Ils pouvaient ainsi répartir les surplus vers les communautés moins florissantes.

Les quipus semblent également avoir constitué un outil de communication dans l'ancien Pérou ; Garcilaso de la Vega, chroniqueur fils d'une princesse inca et d'un noble espagnol, nous rapporte un témoignage d'une telle utilisation. On sait en effet que les chaskis (les hommes à pied qui parcouraient l'Empire pour remettre le courrier) utilisaient les quipus pour mémoriser les messages avec des données qualitatives et quantitatives.

Les quipus pouvant aussi être interprétés comme des messages codés sous la forme de nœuds de différentes sortes sur des fils de laine, coton ou autre matériau et de différentes couleurs, ils servaient aux statistiques de l'État : recensement très précis (nombre d'habitants par âge et par sexe), nombre d'animaux, état des stocks, tributs payés et dus des différents peuples, enregistrement de l'ensemble des entrées et sorties de marchandises des entrepôts de l'État, etc. Seuls les administrateurs connaissaient la clé des quipus : c'étaient les quipucamayocs[9]. Ce système de quipus était aussi utilisé par les dirigeants des provinces pour transmettre les nouvelles importantes à l'Inca[10].

Il semblerait que les quipus aient aussi servi à notifier les grandes dates de l'Histoire et à consigner certains récits ou secrets religieux mais ceux-ci restent indéchiffrables de nos jours contrairement à certains quipus de statistiques.

Le site archéologique de Incahuasi, dont les premiers quipus ont été découverts en 2013, permettra aux scientifiques d'en comparer un grand nombre ainsi que des objets avec lesquels ils ont été découverts. L'un des plus grands experts en quipus, Gary Urton, qui travaille aussi sur le site avec Alejandro Chu, qui a mené les excavations, a déclaré que sans être une véritable pierre de Rosette, il s'agit d'une importante quantité de nouvelles données et qu'il sera possible de bâtir un vocabulaire de base[11].

Pour les plus grands nombres :

où le noyau est une puissance de 10. Donc, les exemples :

• isqon pachak: [9] {100} = 9 ¥ 100 = 900
• qanchis chunka pichqa: [7] {10} + (5) = 75
• kimsa pachak chuska chunka qanchis waranqa ishkay : [[3] {100} ([4] {10} (7))] {1000} (2) = 347002

Le système numérique des Incas est donc de base 10.

Grâce à ce système, on pouvait indiquer les unités, dizaines, centaines, etc. Des recherches récentes en relation avec les yupanas suggèrent qu'elles étaient capables d'exprimer par le calcul des nombres considérables en s'appuyant sur un système non-décimal, mais plutôt en relation avec le nombre 40 ; sommes, restes, multiplications et divisions étaient donc possibles ainsi que l'enregistrement de textes, ce qui emplit d'espoir les chercheurs en quête de la compréhension du fonctionnement des quipus.

La yupana dessinée par Guaman Poma révèle des connaissances astronomiques comme les cycles de Mercure et Vénus; la même yupana permet d'obtenir l'année solaire sidérale inca, dont la précision est impressionnante, et un fantastique calendrier perpétuel, créé autour du chiffre 5[16].

Bien que certains investigateurs aient fait des hypothèses selon lesquelles cet instrument pourrait fonctionner comme un abaque[17] - [18] de calcul, d'autres sont plus sceptiques face à cette éventualité[19]. Néanmoins, le rapport du XVI^e siècle du prêtre espagnol José de Acosta suggèrent que les Incas pouvaient avoir eu un dispositif similaire.

Les chercheurs croient que de telles calculatrices s'appuyaient sur les nombres de Fibonacci pour minimiser la quantité de grains à utiliser par casier[20].

• (en) D'Altroy, Terence. The Incas. Oxford: Blackwell Publishing, 2003.
• (en) Moseley, Michael E. The Incas and Their Ancestors, the Archeology of Peru. London: Thames and Hudson, 1992.
• (en) Thomas E. Gilsdorf, Ethnomathematics of the Inkas, in Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures, Springer-Verlag Berlin Heidelberg DOI: 10.1007/SpringerReference_77966, 2008 (lire en ligne).
• (en) Urton, Gary. At the Crossroads of the Earth and Sky: An Andean Cosmology. Austin: University of Texas Press, 1981.
• (en) Urton, Gary. The Social Life of Numbers, A Quechua Ontology of Numbers and Philosophy of Arithmetic. Austin: University of Texas Press, 1997.