Maillage

Principaux types d'éléments utilisés en 2D.

Principaux types d'éléments utilisés en 3D.

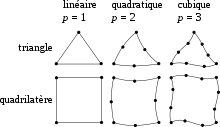
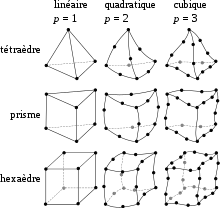
Ce qui suit suffit à définir un maillage non structuré :

• un ensemble de points de l'espace dits sommets du maillage ; dans la pratique, il s'agit d'un tableau de coordonnées
• un ensemble d'éléments ou cellules reliant les sommets entre-eux; dans la pratique, il s'agit d'un - ou plusieurs, dans le cas des maillages hybrides - tableau(x) dit de connectivité

L'espace auquel appartiennent les points est, le plus fréquemment, ${\displaystyle \mathbb {R} ^{2}}$ ou ${\displaystyle \mathbb {R} ^{3}}$. On peut néanmoins parler de maillage 1D, bien que la dimension géométrique du problème est alors réduite à un choix de taille. De la même façon, il existe des maillages de dimension supérieure, particulièrement 4D, permettant, par exemple, de discrétiser le temps de façon non uniforme. Les éléments peuvent être tous de même nature - triangles, par exemple - ou de natures différentes - triangles et quadrilatères - auquel cas le maillage est dit hybride. Le plus fréquent est que les éléments soient linéaires, c'est-à-dire des polytopes conformes à la définition usuelle du triangle, tétraèdre, etc... mais il se peut aussi qu'ils soient polynomiaux de degré 2 ou plus, auquel cas on parle de maillage d'ordre (géométrique) élevé. On parle de maillage conforme d'un domaine ${\displaystyle \Omega }$ lorsque:

• Les éléments recouvrent la fermeture d'${\displaystyle \Omega }$
• L'intersection de deux éléments est soit l'ensemble vide, soit un sommet, soit une arête partagée

Ce cas de figure est, de loin, le plus fréquemment rencontré dans le cadre de la simulation numérique. La seconde condition stipule, en particulier, que deux éléments ne peuvent se chevaucher.

Il est fréquent de retrouver d'autres informations dans un maillage, ou que certaines informations implicites soient explicitées à des fins, notamment, de simplification de lecture. Par exemple, la dimension de l'espace spécifiée en entête de fichier permet de prévoir combien de coordonnées ont les points sans compter les réels entre deux retours à la ligne. Les informations qui suivent sont donc soit spécifiques à des problèmes donnés, soit redondantes mais pratiques:

• nombre d'entités: sommets, cellules...
• la dimension d'espace : typiquement 2D ou 3D ;
• type et degré des éléments/cellules : triangles ${\displaystyle P^{1}}$ ou ${\displaystyle P^{k}}$, quadrilatères (parallélogrammes, rectangles, carrés), …, polygones, en 2D ; tétraèdres, prismes, hexaèdres (parallélépipèdes, cubes), …, polyèdres en 3D ;
• références d'éléments ou de sommets: information entière associée aux entités spécifiant, par exemple, le matériau représenté, le type géométrique d'un sommet (de volume, de surface pure, sur une ligne, un coin, ...), des conditions aux limites pour les problèmes issus de la physique...
• tailles préscrites aux sommets : simple réel ou métrique
• normales aux sommets de surface
• lien vers un objet de CAO

D'autres informations seront, quant à elles, le plus fréquemment calculées à la volée plutôt que stockées. Il en est ainsi de:

• la liste globale des arêtes du maillage : une information n'ayant d'intérêt que lorsqu'on souhaite modifier le maillage, récupérée à l'aide d'une Table de hachage
• le tableau de relations de voisinages des éléments par arête : se calcule à partir d'un tableau d'arêtes construit à cet effet
• les vecteurs normaux aux faces externes (du bord)
• le volume ou l'aire des cellules

Les cellules ci-dessus ont des côtés rectilignes ou des faces planes, elles sont dites « linéaires » (image par une application linéaire de l'élément de référence). On peut aussi utiliser des cellules dites « quadratiques » dont les lignes sont courbes. Chaque côté ou arête est alors défini par trois points : ses extrémités et son point milieu. Les cellules quadratiques permettent de décrire plus fidèlement la frontière de l'objet (on fait l'approximation d'une courbe par une parabole au lieu d'une corde), mais on augmente le nombre de points nécessaires pour décrire une cellule.

Maillage tétraédrique.

Maillage hexaédrique structuré.

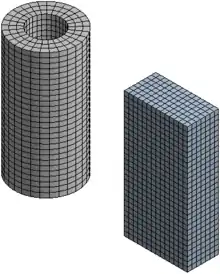
Les maillages les plus « efficaces » sont les maillages dits « réguliers » ou « structurés » : ils sont constitués de parallélogrammes en 2D, et de parallélépipèdes en 3D. Efficace signifie que ces maillages permettent d'économiser les ressources informatiques (mémoire, temps de calcul) :

• dans le cas d'un maillage quelconque, il faut définir la position de chaque nœud, et la composition de chaque polygone ou polyèdre ; la définition est dite explicite ;
• dans le cas d'un maillage régulier, la composition des polygones/polyèdres, voire la position des points, peut être déduites d'une règle de construction, on a une définition dite implicite.

Le cas le plus simple d'un maillage régulier est un empilement de parallélépipèdes rectangles tous identiques ; il suffit de définir :

• un nœud du maillage, appelé « origine » ;
• l'orientation des axes des arêtes ;
• la taille des arêtes selon les trois axes ;
• le nombre d'éléments selon les trois axes.

Par contre, ceci n'est possible que pour des formes ayant des contours simples, de type cylindres (au sens large, incluant les prismes). On peut, si nécessaire, diviser un domaine en sous-domaines ayant des formes simples, et donc avoir plusieurs maillages réguliers, ou bien avoir un maillage régulier au cœur du volume, et avoir une « couche » composée de prismes et tétraèdres à proximité de la surface.

Le maillage le plus simple à réaliser est un découpage en triangles (2D) ou tétraèdres (3D).

Il existe également des logiciels de morphing qui permettent la modification d'un maillage pour diverses utilités.

Les maillages d'ordre élevé sont, en résumé, des maillages dont les éléments sont courbes car polynomiaux. Si, dans le cas linéaire, le domaine d'un triangle de sommets ${\displaystyle P_{100}}$, ${\displaystyle P_{010}}$ et ${\displaystyle P_{001}}$ s'écrit

${\displaystyle \{uP_{100}+vP_{010}+wP_{001},0\leq u,v,w\leq 1,u+v+w=1\}}$,

celui d'un triangle quadratique de sommets ${\displaystyle P_{200}}$, ${\displaystyle P_{020}}$ et ${\displaystyle P_{002}}$ et points de contrôle de Bézier ${\displaystyle P_{110}}$, ${\displaystyle P_{011}}$ et ${\displaystyle P_{101}}$ devient

${\displaystyle \{u^{2}P_{200}+2uvP_{110}+v^{2}P_{020}+2vwP_{011}+w^{2}P_{002}+2wuP_{101},0\leq u,v,w\leq 1,u+v+w=1\}}$,

et est donc intimement lié à l'application

${\displaystyle F_{K}:(u,v)\in {\widehat {K}}\mapsto u^{2}P_{200}+2uvP_{110}+v^{2}P_{020}+2v(1-u-v)P_{011}+(1-u-v)^{2}P_{002}+2(1-u-v)uP_{101}}$,

où ${\displaystyle {\widehat {K}}}$ désigne l'élément de référence, soit le triangle de sommets ${\displaystyle {\widehat {P}}_{1}={\begin{pmatrix}1\\0\end{pmatrix}}}$, ${\displaystyle {\widehat {P}}_{2}={\begin{pmatrix}0\\1\end{pmatrix}}}$, ${\displaystyle {\widehat {P}}_{3}={\begin{pmatrix}0\\0\end{pmatrix}}}$.

Un calcul nécessite avant d'être lancé sur un maillage :

• la vérification des paramètres à respecter du modèle éléments finis
• la pose de conditions aux limites

et permet alors d'approcher et simuler des comportements, éventuellement sur sollicitation, du système, d’où le nom méthode approchée.

Il existe des logiciels de maillage (couramment appelés mailleurs). Ce type de logiciel est fréquemment employé en simulation numérique dans la construction du modèle géométrique, avant sa résolution par un code de calcul, mais aussi parfois en modélisation 3D (graphisme, jeux vidéo, etc.).

À titre d'exemple :

• Gambit
• Gmsh (logiciel libre de maillage par éléments finis)
• MeshLab (logiciel libre de traitement de maillages 3D)

En complément des logiciels de génération de maillage, des logiciels spécifiques (couramment appelés remailleurs) permettent de modifier un maillage existant sans repasser par l'étape de construction du modèle géométrique. Ces logiciels sont utilisés en simulation numérique, notamment pour adapter la taille des entités du maillages (arêtes ou éléments) à une carte de taille fournie par l'utilisateur (issue par exemple d'un estimateur d'erreur a posteriori)[1].

À titre d'exemples :

• HOMARD (logiciel disponible au sein de la plateforme SALOME)
• Mmg
• Omega_h

• Cet article est partiellement ou en totalité issu de l'article intitulé « Mailleur » (voir la liste des auteurs).