K-mer

Le terme k-mer fait généralement référence à toutes les sous-chaînes de longueur k qui sont contenues dans une chaîne de caractère. En génomique computationnelle, les k-mers font référence à toutes les sous-séquences (de longueur k) à partir d'une lecture obtenues par séquençage de l'ADN. La quantité de k-mers possible étant donné une chaîne de caractères de longueur L est $L-k+1$ tandis que le nombre de k-mers étant donné n possibilités (4 dans le cas de l'ADN par exemple ACTG) est $n^{k}$ . Les k-mers sont généralement utilisés lors de l'assemblage de séquences[1], mais peuvent également être utilisés dans l'alignement de la séquence. Dans le contexte du génome humain, les k-mers de différentes longueurs ont été utilisés pour expliquer la variabilité dans les taux de mutation[2] - [3].

L'assemblage de séquences

Aperçu

Dans l'assemblage de séquence, les k-mers sont généralement utilisés lors de la construction de graphiques de De Bruijn. Afin de créer un Graphe de De Bruijn, les chaînes stockées dans chaque arête, de longueur $L$ , doivent se chevaucher l'une l'autre sur une longueur $L-1$ afin de créer un vertex. Les séquences générées à partir de méthode de séquençage de prochaine génération ont généralement différentes longueurs durant une même session de lecture. Par exemple, les séquences lues par la technologie de séquençage Illumina produit des séquences pouvant être capturées par un k-mer de 100. Cependant, le problème avec le séquençage est qu'une petite fraction de k-mers de 100, des 100-mers, présents dans le génome sont en fait réellement générés. Cela est dû à des erreurs de lecture, mais de façon plus importante encore, par de simples trous de couverture qui se produisent au cours du séquençage. Le problème est que ces petites fractions de k-mers "corrompues", violent l'hypothèse principale des graphiques de Bruijn, que tous les k-mer issus des séquences lues doivent se chevaucher aux k-mers dans le génome par une superposition de longueur $k-1$ (qui ne peut pas se produire lorsque tous les k-mers ne sont pas présents). La solution à ce problème est de réduire la taille de ces k-mers en petits k-mers, tels que les petits k-mers représentent tous les k-mers de plus petite taille présents dans le génome. En outre, le fractionnement des k-mers en plus petites tailles aide également à soulager le problème des différentes longueurs de lecture initiale.
Un exemple de la solution de diviser la séquence lue en petits k-mers est montré dans la figure 1. Dans cet exemple, les séquences de 5 nucléotides ne tiennent pas compte de tous les k-mers de longueur 7 du génome, et dans ce cas, un graphe de de Bruijn ne peut pas être créé. Mais quand ils sont divisés en k-mers de longueur 4, les sous-séquences résultantes sont assez nombreuses et variées pour reconstituer le génome à l'aide d'un graphe de de Bruijn.

Cette figure montre le processus de fractionnement de la séquence en petits k-mers (4-mers dans ce cas) afin de pouvoir être utilisés dans un graphe de de Bruijn. (A) Montre le premier segment de l'ADN en cours de séquençage. (B) Montre les lectures qui ont été générées en sortie à partir du séquençage et montre également la façon dont ils se chevauchent. Le problème avec cet alignement est que les séquences se chevauchent sur une longueur de k-2, or elles doivent se chevaucher sur une longueur de k-1 pour être utilisées dans les graphes de de Bruijn. (C) Montre les séquences divisées en plus petites, de 4-mers. (D) Les séquences dupliquées de 4-mers sont écartées et les séquences restantes montrent l'alignement. Notez que ces k-mers se chevauchent sur k-1 et peuvent être utilisés dans un graphe de De Bruijn.

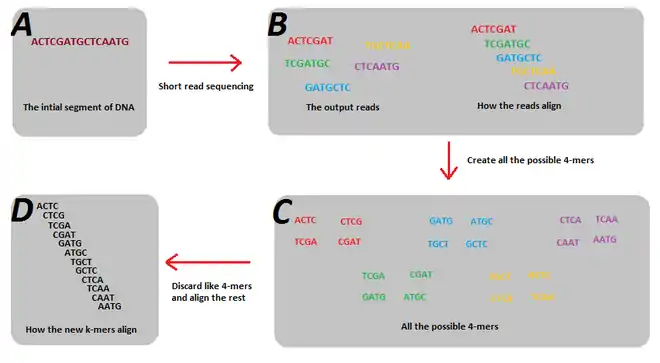
Le choix de la taille des k-mers

Le choix de la taille des k-mers a beaucoup d'effets différents sur l'assemblage des séquences. Ces effets varient grandement entre les plus petites tailles de k-mers et les tailles de k-mers plus grandes. Par conséquent, la compréhension des différentes tailles de k-mers doit être connue afin de choisir une taille appropriée, qui équilibre les effets. Les effets des tailles sont décrits ci-dessous.

Une faible taille de k-mers

Une diminution de la taille des k-mers va diminuer la diversité de séquences stockées dans le graphique dû à la diminution des possibilités de combinaison, et en tant que telle, aide à diminuer la quantité d'espace nécessaire pour stocker une séquence d'ADN.
Avoir une plus petite taille permettra d'augmenter les chances que tous les k-mers se chevauchent, et en tant que telles, les sous-séquences dans le but de construire le graphe de de Bruijn[4].
Cependant, en ayant une taille de k-mers plus petite, on risque d'avoir de nombreux chevauchements dans le graphe pour un seul k-mer. Par conséquent, la reconstruction du génome sera plus difficile car il y aura un nombre plus élevé de chemins ambigus dû à la plus grande quantité de k-mers qui devront être parcourus.
L'information est perdue lorsque les k-mers deviennent plus petits.
- E. g. Les possibilités de combinaison pour AGTCGTAGATGCTG sont inférieures à celles pour ACGT, et en tant que tel, le premier est porteur d'un plus grand nombre d'informations (reportez-vous à l'entropie (la théorie de l'information) pour plus d'informations).
De plus petits k-mers posent le problème de ne pas être en mesure de résoudre certains points dans l'ADN, comme dans les microsatellites où plusieurs répétitions peuvent se produire. C'est à cause du fait que les petits k-mers auront tendance à revenir entièrement sur eux dans ces régions de répétition et il est donc difficile de déterminer le nombre de répétitions qui ont effectivement eut lieu.
- E. g. Pour la sous-suite ATGTGTGTGTGTGTACG, le nombre de répétitions de la TG seront perdues si un k-mer de taille de moins de 16 est choisi. C'est parce que la plupart des k-mers vont revenir dans la région répétée et que le nombre de répétitions du même k-mer sera perdu au lieu de mentionner la quantité de répétitions.

Une grande taille de k-mers

Avoir de plus grande taille de k-mers augmentera la quantité d'arêtes dans le graphe, ce qui, à son tour, va augmenter la quantité de mémoire nécessaire pour stocker la séquence d'ADN.
En augmentant la taille de la k-mer, le nombre de sommets diminuera également. Cela va aider à la construction du génome puisqu'il y aura moins de chemins à parcourir dans le graphique.
Une plus grande taille de k-mer court également un risque plus élevé de ne pas aller vers l'extérieur des sommets de chaque k-mer. C'est pour cette raison qu'une plus grande taille de k-mers augmente le risque qu'ils ne se chevauchent pas avec un autre k-mer sur une longueur de $k-1$ . Par conséquent, cela peut conduire à une non-continuité dans la séquence lue, et en tant que tel, peut conduire à une plus grande quantité de petits contigs.
Une plus grande taille de k-mer aide à atténuer le problème des petites régions de répétition. Cela est dû au fait que le k-mer contiendra un équilibre entre la région de répétition et la séquences d'ADN (étant donné qu'ils sont d'une assez grande taille) qui peuvent aider à résoudre le nombre de répétitions dans ce domaine particulier.

Les applications des k-mers dans l'analyse bio-informatique

La fréquence d'un ensemble de k-mers, dans le génome d'une espèce, dans une région génomique, ou dans une classe de séquences, peut être utilisée en tant que "signature" de sous-séquence. La comparaison de ces fréquences est mathématiquement plus facile que l'alignement de la séquence, et est une méthode importante dans l'alignement sans l'analyse de la séquence. Elle peut également être utilisée comme une première étape d'analyse avant un alignement.

la séparation de différentes espèces dans un mélange de matériel génétique (métagénomique, microbiome)[5] - [6];des phases/cadres d'information peut être ajoutée[7]
Barcoding moléculaire (DNA barcoding) des espèces[8] - [9]
assemblage de novo[10]
classification haplogroupe mitochondriale humaine [11]
détecter le mauvais assemblage de génome[12]
la détection de novo de séquence répétée comme élément transposable[13]
caractériser une protéine de liaison à motif de séquence[14]. En plus de k-mer, incisés k-mers (également nommé écartement q-grammes[15] ou espacées graines[16]) peut également être utilisé [17]
l'identification de mutations ou d'un polymorphisme à l'aide de séquençage de prochaine génération des données[18]
la caractérisation de l'îlot CpG par les régions flanquantes [19] - [20]
détecter des transferts horizontaux [21]
détecter la contamination bactérienne dans un génome eucaryote assemblé [22] - [23]
détecter la recombinaison site [24]
en utilisant la fréquence des k-mers par rapport à la profondeur k-mer à l'estimation de la taille du génome [25] - [26]
estimation de la proportion d'ARN séquencé [27]

Pseudocode

Déterminer la taille de lecture des k-mers peut être fait simplement en bouclant sur la taille de la longueur de la chaîne, en augmentant progressivement la position dans la chaîne et en prenant chaque sous-chaîne de longueur k. Le pseudo-code qui réalise cette opération est comme suit :

fonction K-mer(Chaine_caractere, k) /* k = longueur de chaque k-mer */
    n = longueur(Chaine_caractere)
    /* Boucle sur la longueur de Chaine_caractere jusque la longueur Chaine_caractere - taille des k-mer */
    Pour i = 1 jusque n-k+1 inclus fait :
        /* Sort chaque K-mer de longueur k, de la position i à la position i+k dans Chaine_caractere */
        sortie Chaine_caractere[position i -> position i+k]
    Fin de Boucle
Fin de fonction

En python3, il sera possible d'implémenter le code comme suit :

def kmer(sequence, k) : # sequence correspond a la sequence ADN, k correspond a la longueur des k-mer
    n = len(sequence)
    kmers = []
    for i in range(0,n-k) :
        kmers.append(sequence[i:i+k])
    return kmers

Exemples

Voici quelques exemples montrant les possibles k-mers (en spécifiant une valeur de k) à partir de séquences d'ADN:

Lecture: AGATCGAGTG
3-mers: AGA GAT ATC TCG CGA GAG AGT GTG

5-mers: AGATC GATCG ATCGA TCGAG CGAGT

Lecture: GTAGAGCTGT
5-mers: GTAGA TAGAG AGAGC GAGCT AGCTG GCTGT

Références

P. Compeau, P. Pevzner et G. Teslar, « How to apply de Bruijn graphs to genome assembly », Nature Biotechnology, vol. 29, n^o 11,‎ 2011, p. 987–991 (PMID 22068540, PMCID 5531759, DOI 10.1038/nbt.2023)
Kaitlin E Samocha, Elise B Robinson, Stephan J Sanders et Christine Stevens, « A framework for the interpretation of de novo mutation in human disease », Nature Genetics, vol. 46, n^o 9,‎ 2014, p. 944–950 (ISSN 1061-4036, PMID 25086666, PMCID 4222185, DOI 10.1038/ng.3050)
Varun Aggarwala et Benjamin F Voight, « An expanded sequence context model broadly explains variability in polymorphism levels across the human genome », Nature Genetics, vol. 48, n^o 4,‎ 2016, p. 349–355 (ISSN 1061-4036, PMID 26878723, PMCID 4811712, DOI 10.1038/ng.3511)
Zerbino, Daniel R. et Birney, Ewan, « Velvet: algorithms for de novo short read assembly using de Bruijn graphs », Genome Research, vol. 18, n^o 5,‎ 2008, p. 821–829 (PMID 18349386, PMCID 2336801, DOI 10.1101/gr.074492.107)
"Rachid Ounit, Steve Wanamaker, Timothy J Close and Stefano Lonardi", « CLARK: fast and accurate classification of metagenomic and genomic sequences using discriminative k-mers », BMC Genomics, vol. 16,‎ 2015, p. 236 (PMID 25879410, PMCID 4428112, DOI 10.1186/s12864-015-1419-2)
Dubinkina, Ischenko, Ulyantsev, Tyakht, Alexeev, « Assessment of k-mer spectrum applicability for metagenomic dissimilarity analysis », BMC Bioinformatics, vol. 17,‎ 2016, p. 38 (PMID 26774270, PMCID 4715287, DOI 10.1186/s12859-015-0875-7)
Zhu, Zheng, « Self-organizing approach for meta-genomes », Computational Biology and Chemistry, vol. 53,‎ 2014, p. 118–124 (PMID 25213854, DOI 10.1016/j.compbiolchem.2014.08.016)
Chor, Horn, Goldman, Levy, Massingham, « Genomic DNA k-mer spectra: models and modalities », Genome Biology, vol. 10, n^o 10,‎ 2009, R108 (PMID 19814784, PMCID 2784323, DOI 10.1186/gb-2009-10-10-r108)
Meher, Sahu, Rao, « Identification of species based on DNA barcode using k-mer feature vector and Random forest classifier », Gene, vol. 592, n^o 2,‎ 2016, p. 316–324 (PMID 27393648, DOI 10.1016/j.gene.2016.07.010)
Li et al, « De novo assembly of human genomes with massively parallel short read sequencing », Genome Research, vol. 20, n^o 2,‎ 2010, p. 265–272 (PMID 20019144, PMCID 2813482, DOI 10.1101/gr.097261.109)
Navarro-Gomez et al, « Phy-Mer: a novel alignment-free and reference-independent mitochondrial haplogroup classifier », Bioinformatics, vol. 31, n^o 8,‎ 2015, p. 1310–1312 (PMID 25505086, PMCID 4393525, DOI 10.1093/bioinformatics/btu825)
Phillippy, Schatz, Pop, « Genome assembly forensics: finding the elusive mis-assembly », Bioinformatics, vol. 9, n^o 3,‎ 2008, R55 (PMID 18341692, PMCID 2397507, DOI 10.1186/gb-2008-9-3-r55)
Price, Jones, Pevzner, « De novo identification of repeat families in large genomes », Bioinformatics, vol. 21(supp 1),‎ 2005, i351–8 (PMID 15961478, DOI 10.1093/bioinformatics/bti1018)
Newburger, Bulyk, « UniPROBE: an online database of protein binding microarray data on protein–DNA interactions », Nucleic Acids Research, vol. 37(supp 1), n^o Database issue,‎ 2009, D77–82 (PMID 18842628, PMCID 2686578, DOI 10.1093/nar/gkn660)
Better filtering with gapped q-grams, vol. 56, coll. « Lecture Notes in Computer Science » (n^o 1–2), 2002, 51–70 p. (ISBN 978-3-540-43862-5, DOI 10.1007/3-540-45452-7_19, lire en ligne)
Keich et al, « On spaced seeds for similarity search », Discrete Applied Mathematics, vol. 138, n^o 3,‎ 2004, p. 253–263 (DOI 10.1016/S0166-218X(03)00382-2)
Ghandi et al, « Enhanced regulatory sequence prediction using gapped k-mer features », PLoS Computational Biology, vol. 10, n^o 7,‎ 2014, e1003711 (PMID 25033408, PMCID 4102394, DOI 10.1371/journal.pcbi.1003711, Bibcode 2014PLSCB..10E3711G)
Nordstrom et al, « Mutation identification by direct comparison of whole-genome sequencing data from mutant and wild-type individuals using k-mers », Nature Biotechnology, vol. 31, n^o 4,‎ 2013, p. 325–330 (PMID 23475072, DOI 10.1038/nbt.2515)
Chae et al, « Comparative analysis using K-mer and K-flank patterns provides evidence for CpG island sequence evolution in mammalian genomes », Nucleic Acids Research, vol. 41, n^o 9,‎ 2013, p. 4783–4791 (PMID 23519616, PMCID 3643570, DOI 10.1093/nar/gkt144)
Mohamed Hashim, Abdullah, « Rare k-mer DNA: Identification of sequence motifs and prediction of CpG island and promoter », Journal of Theoretical Biology, vol. 387,‎ 2015, p. 88–100 (PMID 26427337, DOI 10.1016/j.jtbi.2015.09.014)
Jaron, Moravec, Martinkova, « SigHunt: horizontal gene transfer finder optimized for eukaryotic genomes », Bioinformatics, vol. 30, n^o 8,‎ 2014, p. 1081–1086 (PMID 24371153, DOI 10.1093/bioinformatics/btt727)
Delmont, Eren, « Identifying contamination with advanced visualization and analysis practices: metagenomic approaches for eukaryotic genome assemblies », PeerJ, vol. 4,‎ 2016, e1839 (DOI 10.7717/Fpeerj.1839)
Bemm et al, « Genome of a tardigrade: Horizontal gene transfer or bacterial contamination? », Proceedings of the National Academy of Sciences, vol. 113, n^o 22,‎ 2016, E3054–E3056 (PMID 27173902, PMCID 4896698, DOI 10.1073/pnas.1525116113)
Wang, Xu, Liu, « Recombination spot identification Based on gapped k-mers », Scientific Reports, vol. 6,‎ 2016, p. 23934 (PMID 27030570, PMCID 4814916, DOI 10.1038/srep23934, Bibcode 2016NatSR...623934W)
Hozza, Vinar, Brejova « How big is that genome? estimating genomesize and coverage from k-mer abundance spectra » (2015) (DOI 10.1007/978-3-319-23826-5_20)
—SPIRE 2015
Lamichhaney et al, « Structural genomic changes underlie alternative reproductive strategies in the ruff (Philomachus pugnax) », Nature Genetics, vol. 48, n^o 1,‎ 2016, p. 84–88 (PMID 26569123, DOI 10.1038/ng.3430)
Patro, Mount, Kingsford, « Sailfish enables alignment-free isoform quantification from RNA-seq reads using lightweight algorithms », Nature Biotechnology, vol. 32, n^o 5,‎ 2014, p. 462–464 (PMID 24752080, PMCID 4077321, DOI 10.1038/nbt.2862, arXiv 1308.3700)

Liens externes

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.