Image matricielle

Une image matricielle doit généralement se définir par :

• Les dimensions de sa matrice : soit sa largeur et sa hauteur (voire sa profondeur dans le cas d'images tridimensionnelles), soit l'une ou l'autre plus le nombre total de points la constituant. Dans ce dernier cas, la (ou les) dimension manquante pourra être déduite via la division du nombre total de points par le nombre de points dans la dimension connue.

Exemple : Soit une image de 300 points de large. Si elle possède au total 60 000 points de couleur, alors nous savons que sa hauteur sera constituée de : 60 000 divisé par 300 = 200 points de couleur sur sa hauteur.

• Sa taille réelle : en effet, une matrice de points n'est qu'un concept abstrait en soi. Lors de son application, il peut être nécessaire de connaître précisément la taille réelle que doit revêtir l'image dans la réalité de son application. De cette surface déterminée dépendra les dimensions réelles de chaque point théorique la constituant. Ceci n'a de sens que si l'unité de surface employée est connue (comme le centimètre ou le pouce) et que l'image s'inscrit dans les contraintes d'une réalité physique tangible. À noter que la taille de la surface réelle que l'image doit couvrir n'est pas nécessairement en corrélation directe avec les dimensions de sa matrice du fait même des très nombreuses formes que peuvent revêtir physiquement ses points. Ces derniers pourront tout aussi bien être parfaitement ronds et de taille identique, leur espacement vertical et horizontal différant l'un de l'autre que de taille et de forme (hexagones ou autre) variables afin de s'adapter à la surface réelle pour la recouvrir entièrement. En réalité, ce facteur est souvent donné à titre indicatif afin d'adapter le système de reproduction qui, lui, pourra utiliser un système pouvant être totalement différent de celui des matrices de points. Autrement dit, les dimensions de la matrice de points ne peuvent pas, à elles seules, définir les proportions réelles de l'image (telle qu'originalement conçue) bien que, en règle générale et pour des questions pratiques, l'on considère chaque point comme pouvant être contenu dans un carré.
• La nature de ses couleurs : généralement, il s'agit de la mention d'un standard faisant référence à un système colorimétrique connu. Mais rien n'interdit l'évocation d'un système colorimétrique relatif à autre chose (par exemple, d'un nombre de gradient pouvant être obtenu par un mélange pigmentaire spécifique). La plupart des images numériques utilisent les différents systèmes RVB, HLS, TLS, HUV ou quadrichromique : Cyan Magenta Yellow Black.
• Le nombre et la profondeur/précision de ses couleurs : soit en précisant une palette de couleurs, soit en indiquant une précision des intensités des composantes utilisées par les canaux de la vidéo soit le rouge le vert le bleu ou selon la codification du système chromatique précité. Exprimer en fonction du nombre de bits d'adressage sur chacun des canaux de la vidéo en bit. 1/2/4/8/10/12/16... avec des puissances de deux. Une image de 320 x 200 pixels en monochrome 320 x 200 / 8 bits = 2 000 octets. Avec 8 couleurs différentes on obtient 16 kilo-octets. Avec 256 couleurs on détermine la mémoire nécessaire comme étant d'une plage de 64 kilo-octets avec cette résolution. Une image en monochrome de 8 pouces par 12 pouces avec une résolution de 300 ppp donne 8 x 12 x 300 x 300 / 8 soit 1 080 000 : une taille égale à la mémoire de presque 1 méga-octet. Les imprimantes laser ont obtenu une capacité mémoire suffisante pour mémoriser une page équivalent au format A4 à partir de la fin des années 1980. De façon encore plus étrange le poids en octets d'une image 24 bits est égale à 320 x 200 x 3 = 192 000 octets différents car 3 octets sont nécessaires pour coder 24 bits (3 x 8 = 24) sans compression de l'image. Formule : le poids en octets d'une image est égale à sa surface multiplié par le nombre de bits par pixel et de canaux.
• Des informations complémentaires telles que, typiquement :
  • l'auteur de l'image et sa date de création
  • les spécificités techniques pour lesquelles - ou, desquelles - elle a été conçue - ou elle provient (exemple : forme de pixels, données d'étalonnage colorimétrique, ...)
  • une miniature afin de pouvoir être prévisualisée plus facilement
  • etc.

Le codage ou la représentation informatique d'une image implique sa numérisation. Cette numérisation se fait dans deux espaces :

• l'espace spatial où l'image est numérisée suivant l'axe des abscisses et des ordonnées : on parle d'échantillonnage. Les échantillons dans cet espace sont nommés pixels et leur nombre va constituer la définition de l'image.
• l'espace des couleurs où les différentes valeurs de luminosité que peut prendre un pixel sont numérisées pour représenter sa couleur et son intensité ; on parle de quantification. La précision dans cet espace dépend du nombre de bits sur lesquels on code la luminosité et est appelée profondeur de l'image.

La qualité d'une image matricielle est déterminée par le nombre total de pixels (« picture element ») et la quantité d’information contenue dans chaque pixel (souvent appelée profondeur de numérisation des couleurs).

La définition d'une image avec sa notion connexe de résolution définit le niveau de détails qui seront visibles dans l'image. Pour une taille donnée, plus il y aura de pixels, plus il y aura de détails fins visibles. On dit que plus une image a de pixels, plus elle est de grande qualité. Une image numérisée avec une définition de 640 × 480 pixels (donc contenant 307 200 pixels) apparaîtra très approximative et sous forme d’un pavage de petits carrés de couleur, par comparaison à une image de 1280 × 1024 px (soit 1 310 720 pixels).

Puisqu'il coûte une grande quantité de données pour stocker une image de très grande qualité, des techniques de compression de données sont souvent employées pour réduire la taille des images stockées sur un disque. Certaines de ces techniques perdent des informations, et ainsi appauvrissent la qualité de l’image, afin de réaliser un fichier occupant beaucoup moins de place sur disque. Les techniques de compression qui perdent des informations sont dites de compression avec pertes.

Le smiley dans le coin supérieur gauche est une image bitmap. Lorsqu'elle est élargie, les pixels individuels s'affichent sous forme de carrés. Zoomez plus fort, pour pouvoir les analyser, leurs couleurs sont construites en ajoutant les valeurs de rouge, vert et bleu.

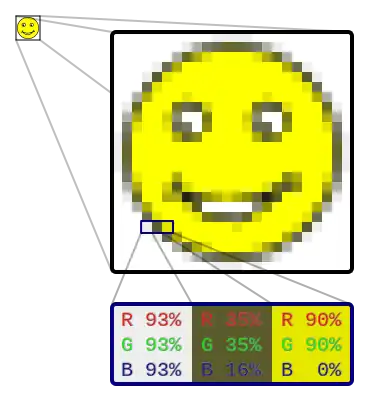
Une image peut contenir une palette pour définir la couleur de chaque pixel. À chaque pixel est associé le rang qu’occupe sa couleur dans la palette. C’est le cas des images GIF qui possèdent une palette supportant jusqu’à 256 couleurs.

Les images délivrées par les appareils photo et les logiciels de dessins sont, elles, une fois décompressées, codées pour chaque pixel par un triplet de valeurs pour le rouge, le vert et le bleu (modèle RVB). Chaque canal est codé (pour les images JPEG) sur 8 bits selon son intensité. Sur 8 bits, il est possible de définir 256 niveaux (2 puissance 8). On obtient en fin de compte une image de 16,777216 millions de teintes disponibles (256 puissance 3). On parle alors d'une image en 16 millions de couleurs.

Il faut distinguer les différentes représentations d'une image matricielle.

• Dans un fichier, pour le stockage et l'échange. Dans ce cas, l'image est le plus souvent compressée et stockée dans un format graphique. Les principaux formats matriciels sont BMP, GIF, TIFF, PNG et JPEG.
• Le format PPM est aussi parfois utilisé car il a l'avantage de coder très simplement l'image.
• En mémoire graphique de l'ordinateur ou de la carte graphique. Ce format est généralement sans aucune compression pour pouvoir être directement exploitable et affichable sur l'écran.

Lorsque l'on grossit une image matricielle, puisqu'on ne rajoute aucune information qui ne serait pas déjà présente, cela induit une perte de qualité visible. Plus exactement, une fois qu'une image est numérisée, sa définition est fixe et son aspect visuel ne peut pas s'améliorer, même en utilisant de meilleurs dispositifs d'affichage ou astuces d'affichage. Une image numérique agrandie est dite pixelisée.

En revanche, les images vectorielles peuvent facilement s’afficher sous différentes échelles et s’adaptent à la qualité du dispositif d’affichage. Malgré cela, les images matricielles sont plus appropriées que les images vectorielles aux travaux sur photographies ou sur photos réalistes car il est aujourd'hui impossible en pratique d'obtenir une image vectorielle à partir d'une photo, même si des recherches ont lieu sur ce sujet en analyse d'image.

Une image vectorielle ne peut pas être affichée directement sur un écran. Elle doit auparavant être transformée en image de type bitmap, seul type qui soit exploitable par la carte graphique. Tous les logiciels qui produisent des images vectorielles (notamment les logiciels de dessin industriel) réalisent cette transformation.

À la fin du XX^e siècle, les moniteurs d'ordinateur pouvaient afficher environ entre 72 et 96 PPP (ou dpi (Dots Per Inch) en anglais, soit 28 à 38 points par centimètre), alors que les imprimantes modernes peuvent atteindre des résolutions de 600 dpi (236 points par cm) voire plus ; ainsi travailler avec des images destinées à l’impression peut s’avérer difficile ou exiger de grands moniteurs et des ordinateurs très puissants. Les moniteurs avec des résolutions de 200 dpi (79 points par cm) furent disponibles pour le grand public vers la fin de 2001.

Les images destinées à l'impression professionnelle sont travaillées à 300 dpi (118 points par cm) et en CMJN (cyan, magenta, jaune, noir, représentation par synthèse soustractive). Elles occupent entre une vingtaine de mégaoctets (~20 Mo) et plus de 100. Le RVB est une palette d'affichage qui correspond à la synthèse additive.

Notons qu'une image de 640 × 480 sur un écran de 36 cm (14") a une résolution de 22,2 points par cm, soit 56 dpi. Une image de 1 600 × 1 200 sur un écran de 53 cm (21") a une résolution de 38 points par cm, soit 96 dpi.