Fonction quasi périodique

En mathématiques, une fonction quasi périodique est une fonction qui vérifie une équation fonctionnelle proche de celle qui caractérise une fonction périodique. Une fonction ${\displaystyle f}$ est quasi périodique de quasi période ${\displaystyle \omega }$ si ${\displaystyle f(z+\omega )=g(z,f(z))}$, où ${\displaystyle g}$ est une fonction " plus simple " que ${\displaystyle f}$ , au sens large.

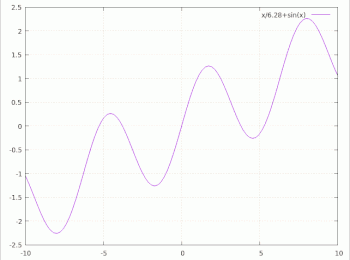
Un cas simple (parfois appelé quasi périodique arithmétique) est si la fonction obéit à l'équation :

${\displaystyle f(z+\omega )=f(z)+C}$

Un autre cas (parfois appelé quasi périodique géométrique) est si la fonction obéit à l'équation :

${\displaystyle f(z+\omega )=Cf(z)}$

Un exemple de fonction quai périodique géométrique est la fonction thêta de Jacobi, où

${\displaystyle \vartheta (z+\tau$ ;\tau )={\rm {e}}^{-2{\rm {i}}\pi z-{\rm {i}}\pi \tau }\vartheta (z;\tau ),}

montre que pour fixe ${\displaystyle \tau }$ il a une quasi-période ${\displaystyle \tau }$ ; il est également périodique avec une période un. Un autre exemple est fourni par la fonction sigma de Weierstrass, qui est quasi périodique en deux quasi périodes indépendantes, les périodes de la fonction ℘ de Weierstrass correspondante.

Des fonctions avec une équation fonctionnelle additive

${\displaystyle f(z+\omega )=f(z)+az+b\ }$

sont aussi appelés quasi périodiques. Un exemple de fonctions de ce type est la fonction zêta de Weierstrass, où

${\displaystyle \zeta (z+\omega ,\Lambda )=\zeta (z,\Lambda )+\eta (\omega ,\Lambda )\ }$

pour un fonction η indépendante de z lorsque ω est une période de la fonction de Weierstrass ℘ correspondante.

Dans le cas particulier où ${\displaystyle f(z+\omega )=f(z)\ }$ on dit que f est périodique de période ω dans le réseau de périodes ${\displaystyle \Lambda }$ .

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.