Dessin d'enfant (mathématiques)
En mathématiques, les dessins d'enfants, tels qu'ils ont été introduits par Alexandre Grothendieck dans son Esquisse d'un programme, sont des objets combinatoires permettant d'énumérer de manière simple et élégante les classes d'isomorphisme de revêtements étales de la droite projective privée de trois points. Le groupe de Galois absolu opérant de manière naturelle sur de tels revêtements, le but de la théorie des dessins d'enfants est de traduire cette action en termes combinatoires.
Combinatoire
Un dessin d'enfant est un graphe abstrait connexe muni de deux structures additionnelles :
- Une structure bipartite sur ses sommets, c.-à-d. une distinction entre sommets blancs et noirs de telle sorte que les extrémités d'une arête n'aient jamais la même couleur ;
- Un ordre cyclique des arêtes concourantes en un même sommet.
La première de ces deux conditions implique, par exemple, que le graphe ne possède pas de boucle (arête ayant les deux extrémités qui coïncident). L'ordre cyclique est crucial dans la définition ; en guise d'exemple, les deux derniers dessins sur la droite de la figure 1 sont distincts tout en correspondant au même graphe abstrait.
Le degré d'un dessin d'enfant est le nombre d'arêtes qui le composent. La valence d'un sommet est le nombre d'arêtes auxquelles il appartient. Le degré est donc égal à la somme des valences des sommets blancs (ou la somme des valences des sommets noirs). Il existe un nombre fini de dessins d'enfants de degré fixé.

Topologie
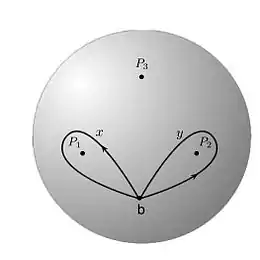
Soit la sphère privée de trois points et . Ayant fixé un point base de , le groupe fondamental topologique est libre, engendré par deux éléments. De manière plus précise, les lacets simples et autour de et constituent des générateurs canoniques de , le lacet autour de étant obtenu par la relation . On rappelle qu'il existe une bijection entre l'ensemble des classes d'isomorphie de revêtements topologiques (finis) de et les classes de conjugaison de sous-groupes d'indice fini de .
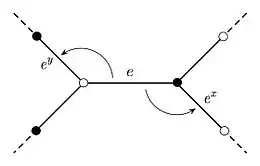
Étant donné un dessin d'enfant, il est maintenant possible de définir une action à droite de sur l'ensemble de ses arêtes : le générateur (resp. ) envoie une arête sur la première arête obtenue en tournant en sens anti-horaire autour du sommet noir (resp. blanc) de . Cette action, décrite dans la figure 3, est appelée action de monodromie; elle est transitive, car le graphe sous-jacent au dessin d'enfant est supposé connexe. En particulier, les stabilisateurs des arêtes sont des sous-groupes conjugués de d'indice égal au degré du dessin d'enfant. On associe donc à un dessin d'enfant une classe de conjugaison de sous-groupes de . Réciproquement, étant donné une telle classe de conjugaison , il est possible de lui associer un dessin d'enfant: ses arêtes sont par définition les éléments de l'ensemble des classes à droite d'un représentant de . La multiplication à droite par un élément de définit une action sur et deux arêtes ont un sommet noir (resp. blanc) en commun si et seulement si elles appartiennent à la même orbite sous l'action du sous-groupe de engendré par (resp. par ). On vérifie facilement que ces constructions sont inverses l'une de l'autre. En résumé, on obtient la
Proposition/construction. Il existe une bijection entre l'ensemble des dessins d'enfants et l'ensemble des classes d'isomorphie de revêtements topologiques finis de la sphère privée de trois points.
Le paragraphe suivant propose une description plus visuelle et intuitive de cette correspondance.
Surfaces de Riemann
Il est possible de munir la surface topologique introduite dans le paragraphe précédent d'une structure de surface de Riemann, unique à isomorphisme près : elle est en effet isomorphe à la sphère de Riemann privée de trois points, que l'on peut supposer être et . Il s'ensuit que si est un revêtement topologique, il existe une structure de surface de Riemann sur , unique à isomorphisme près, telle que induise un revêtement de surfaces de Riemann. La surface de Riemann possède une unique compactification , et le morphisme se prolonge de manière unique en un revêtement de la sphère de Riemann uniquement ramifié au-dessus des points et . Un tel revêtement est appelé application de Belyi et le couple est une paire de Belyi.
Soit maintenant une application de Belyi. Le dessin d'enfant correspondant peut se réaliser concrètement en considérant la préimage via de l'intervalle unité . Tout d'abord, est un complexe simplicial de dimension i.e. un graphe. L'ordre cyclique sur les arêtes concourantes en un même sommet est induit par l'orientation de la surface de Riemann . Les sommets noirs (resp. blancs) sont les éléments de la fibre (resp. ). Leur valence n'est autre que l'indice de ramification du point correspondant. Le complémentaire de est union disjointe de domaines, isomorphes à des disques (en tant que surfaces de Riemann) ; ce sont les faces du dessin d'enfant. Dans le contexte des surfaces de Riemann, la proposition de la section précédente peut alors se reformuler de la manière suivante :
Proposition. Il existe une bijection entre l'ensemble des dessins d'enfants et l'ensemble des classes d'isomorphie d'applications de Belyi.
Courbes algébriques
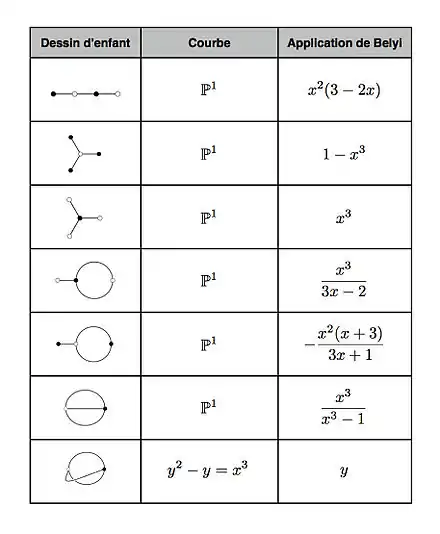
Le théorème d'existence de Riemann, et plus généralement les théorèmes d'algébrisation GAGA affirment que tout revêtement fini de la sphère de Riemann se réalise par analytification d'un revêtement de la droite projective. En particulier si est une paire de Belyi (cf. le paragraphe précédent), on peut supposer que est une courbe algébrique (projective, lisse) définie sur (cf Théorème de Belyi et action galoisienne). On peut alors parler des équations d'un dessin d'enfant : ce sont celles qui définissent la courbe d'une part, et celles qui définissent le revêtement de l'autre. Il est important de remarquer que ces équations ne sont pas uniques. Il est assez facile d'obtenir les équations des dessins d'enfant ayant un degré relativement petit, mais le cas général se révèle bien plus difficile. La figure 4 fournit la liste des équations des dessins d'enfants de degré .
Action galoisienne
Il est naturel de se demander quelles courbes se réalisent comme revêtements de la droite projective non ramifiés en dehors de trois points. La réponse est fournie par le célèbre théorème de Belyi, qui peut être considéré comme une uniformisation arithmetique pour les courbes algébriques :
Théorème (Belyi). Soit une courbe projective lisse définie sur . Les conditions suivantes sont équivalentes:
- - Il existe une application de Belyi ,
- - La courbe peut être définie sur (i.e. il existe une courbe définie sur telle que la courbe obtenue par extension des scalaires de à soit isomorphe à ).
Ce résultat affirme que tout dessin d'enfant possède des équations dont les coefficients sont des nombres algébriques. De plus, on peut montrer que si deux applications de Belyi définies sur sont isomorphes sur , alors elles le sont déjà sur . Il est alors possible de définir une action du groupe de Galois absolu sur les dessins d'enfants : fixons une application de Belyi définie sur associée à un dessin d'enfant . Pour tout élément , le revêtement obtenu en faisant agir sur les coefficients définissant est encore une application de Belyi. Le dessin d'enfant correspondant, noté , est appelé conjugué galoisien de . L'un des objectifs de la théorie des dessins d'enfants de Grothendieck est de décrire cette action en termes combinatoires.
Notes et références
Voir aussi
Bibliographie
- Belyĭ, G. V., Galois extensions of a maximal cyclotomic field. Izv. Akad. Nauk SSSR Ser. Mat. 43 (1979), no. 2, 267–276.
- Grothendieck, A., Esquisse d'un programme. London Math. Soc. Lecture Note Ser., 242, Geometric Galois actions, 1, 5–48, Cambridge Univ. Press, Cambridge, 1997.
- Serre, J.-P., Géométrie algébrique et géométrie analytique. Ann. Inst. Fourier, Grenoble 6 (1955--1956), 1–42.




























![{\displaystyle [0,1]\subset {\hat {\mathbb {C} }}}](https://img.franco.wiki/i/9eac709e5a9624c8bf4956850f2ef5e0b619c6cd.svg)














