Courbure positive

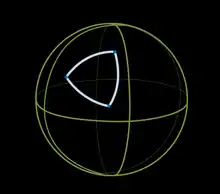
Soit une variété riemannienne (M,g) ; on sait qu'en chaque point m de la variété, à toute famille libre (X,Y) de vecteurs tangents en m on peut associer la courbure sectionnelle ${\displaystyle K_{m}(X,Y)}$. Ce réel ne dépend que du 2-plan P engendré par X et Y et peut être calculé à partir du tenseur de courbure (et réciproquement) ; il généralise la notion de courbure de Gauss d'une surface. La variété est dite à courbure positive (respectivement strictement positive) quand, en chaque point, sa courbure sectionnelle est positive (respectivement strictement positive). Il en existe une interprétation géométrique soimple : en courbure strictement positive, au voisinage de chaque point, les géodésiques (images des droites issues de l'origine) s'écartent moins vite que dans le cas euclidien, les cercles géodésiques (images des cercles concentriques) sont de périmètre moins élevé[3], les disques géodésiques d'aire moins importante.

On dispose d'un nombre très limité d'exemples de variétés à courbure strictement positive et on n'en connaît que pour des dimensions assez spécifiques :

- un certain nombre sont des espaces homogènes : les sphères, les différents espaces projectifs, deux espaces exceptionnels de dimension 7 et 13, et une famille d'espaces de dimension 7, les variétés d'Aloff-Wallach

- il existe également des familles non homogènes, en dimension 6, 7 et 13

- il faut bien entendu ajouter les petites déformations de ces exemples.

Si on se limite à l'hypothèse de positivité, un certain nombre d'autres exemples sont connus, notamment parmi les espaces symétriques ou les espaces homogènes[4]. Pour autant, on ne dispose d'aucun critère topologique permettant de tracer la frontière entre les domaines de la courbure positive ou strictement positive. De fait, dans son influente sélection de problèmes ouverts éditée en 1982, Shing-Tung Yau fait remarquer qu'on est incapable de citer un exemple de variété (compacte, simplement connexe) admettant une structure riemannienne de courbure positive et aucune de courbure strictement positive. La conjecture de Hopf (en), qui porte sur l'existence d'une courbure strictement positive sur ${\displaystyle \mathbb {S} ^{2}\times \mathbb {S} ^{2}}$, en est l'illustration la plus célèbre[5].

La courbure de Ricci est une contraction du tenseur de courbure ; elle constitue une forme bilinéaire symétrique sur les vecteurs tangents. La quantité ${\displaystyle \mathrm {Ric} (X,X)}$ s'analyse comme une moyenne des courbures sectionnelles des plans contenant le vecteur X. On peut à nouveau donner une interprétation géométrique de la stricte positivité : lorsque ${\displaystyle \mathrm {Ric} (X,X)>0}$, l'image d'un cône d'axe X par l'application exponentielle a son volume qui tend à diminuer (toujours au plan infinitésimal). La positivité de la courbure de Ricci se traduit donc par le rétrécissement des volumes des boules, phénomène qu'on retrouve à l'échelle globale et qui est quantifié par l'inégalité de Bishop-Gromov.

La propriété de positivité de la courbure de Ricci s'est révélée progressivement plus contraignante que ce qui était d'abord anticipé, et de nombreux résultats faisant intervenir cette courbure sont venus doubler les résultats analogues en courbure sectionnelle. Les deux hypothèses seront donc présentées de façon parallèle ci-dessous.

La courbure scalaire s'obtient par une nouvelle contraction de la courbure de Ricci. Elle se traduit par la donnée d'une valeur numérique en chaque point, qu'on peut à nouveau considérer comme une forme de moyenne des courbures de Ricci. Hormis en dimension 2 où elle représente la totalité de la courbure (courbure de Gauss), elle donne en général une information très partielle sur la courbure et n'entraîne pas de contrainte très forte sur la variété sous-jacente.

La question de la prescription de la valeur de la courbure scalaire a été envisagée et résolue de façon très générale. On sait classer les variétés compactes de dimension supérieure à 3 en trois catégories suivant le type de courbure scalaire qu'elles peuvent porter[6]

- celles qui peuvent porter une courbure scalaire arbitraire (toute fonction régulière est la courbure scalaire d'une certaine métrique) ;

- celles qui ont pour courbures scalaires possibles toute fonction ayant au moins une valeur strictement négative ;

- et celles pour lesquelles on retrouve les mêmes que dans la catégorie précédente, plus la fonction nulle.

On voit notamment qu'il est toujours possible de réaliser une courbure scalaire strictement négative. En revanche, seule la première catégorie peut porter une courbure scalaire strictement positive (et alors elle en porte une qui est constante). Cette première catégorie a été totalement caractérisée : en dimension 5 et plus, les variétés compactes simplement connexes qui portent une telle métrique sont

- les variétés non spin

- et les variétés de spin dont le α-genre est nul[7].

Les propriétés de cet invariant font que l'existence est garantie en dimension d congrue à 0, 1,2 ou 4 modulo 8. En dimension 4, il existe une autre contrainte pour l'existence, l'annulation des invariants de Seiberg-Witten[8].

Lorsque la courbure sectionnelle est positive, le resserrement des géodésiques est non seulement une tendance infinitésimale, mais en fait un phénomène global, quantifiable par le Théorème de comparaison de Toponogov. Cela laisse imaginer que dans le domaine de la courbure positive, la variété pourrait se refermer sur elle-même. Le théorème de Bonnet-Schoenberg-Myers va dans ce sens : il montre qu'une variété dont la courbure est toujours supérieure à une constante strictement positive est compacte, et donne une borne explicite sur son diamètre.

En sens inverse, on note qu'il existe des variétés non compactes à courbure positive, comme un paraboloïde de l'espace euclidien de dimension 3 (dans ce cas, la courbure tend vers 0 à l'infini).

Le théorème de l'âme permet essentiellement de ramener l'étude d'une variété M à courbure sectionnelle positive au cas compact. En effet M possède une âme, c'est-à-dire une sous-variété N compacte, totalement géodésique et totalement convexe telle que M est difféomorphe au fibré normal de N. L'âme n'est pas unique, mais deux âmes sont toujours isométriques[9]. Un résultat limite de Perelman montre qu'il y a une dichotomie entre des formes cylindriques ou paraboliques, ou plus précisément

- les variétés ayant une âme non triviale, et hors de la direction de laquelle la courbure sectionnelle est toujours nulle,

- et les variétés d'âme réduite à un point, difféomorphes à ${\displaystyle \mathbb {R} ^{n}}$.

Une version de ces résultats subsiste en courbure de Ricci positive : l'outil de comparaison géométrique est cette fois l'inégalité de Bishop-Gromov donnant l'évolution du volume des boules. On retrouve une implication entre la minoration de la courbure (de Ricci cette fois) par une constante et la compacité de la variété ; il s'agit donc d'un renforcement du théorème de Bonnet-Schoenberg-Myers. Le théorème de décomposition de Cheeger et Gromoll, peut être comparé au théorème de l'âme : il énonce qu'en courbure de Ricci positive, à chaque fois qu'on trouve une ligne géodésique (c'est-à-dire une géodésique qui minimise toujours la longueur entre deux de ses points), la variété est isométrique à un produit cartésien ${\displaystyle N\times \mathbb {R} }$[10].

En vertu des résultats précédents, la question de la topologie se concentre en général sur l'étude des variétés compactes. Elle peut s'envisager dans deux directions opposées : quelles contraintes tirer d'une information de positivité de la courbure ? et en sens inverse, quelles variétés admettent une courbure positive ?

On dispose de résultats partiels pour répondre à la première question au moins pour la courbure sectionnelle strictement positive : une conséquence du théorème de Bonnet-Schoenberg-Myers déjà mentionné est qu'une variété compacte de courbure sectionnelle strictement positive, voire de courbure de Ricci strictement positive, admet un groupe fondamental fini. En dimension paire, et sous l'hypothèse de courbure sectionnelle strictement positive, le théorème de Synge précise qu'il ne peut être que trivial ou égal à ${\displaystyle \mathbb {Z} /2\mathbb {Z} }$[11]. En revanche en dimension impaire, l'exemple des espaces lenticulaires montre qu'il y a plus de situations possibles.

Sous certaines hypothèses plus fortes de pincement de la courbure, la topologie peut être entièrement caractérisée : ainsi si la courbure sectionnelle est strictement comprise entre 1 et 4, la variété est difféomorphe à une sphère. C'est le théorème de la sphère, démontré en 2007 dans sa version différentiable.

En vertu de ses propriétés de symétrie, le tenseur de courbure de Riemann peut être vu comme une forme bilinéaire symétrique sur les 2-formes

${\displaystyle R^{\ast }:\Lambda ^{2}(TM)\times \Lambda ^{2}(TM)\to \mathbb {R} .}$

Avec les identifications usuelles dans le cadre euclidien, on peut aussi considérer cela comme un opérateur autoadjoint sur ${\displaystyle \Lambda ^{2}(TM)}$.

La positivité de cet opérateur est contrainte plus forte que celle de la courbure sectionnelle et se révèle en fait très forte. Ainsi une variété simplement connexe à opérateur de courbure strictement positif est homéomorphe à une sphère selon un résultat de 1988 de Micallef et Moore[13]. La question d'en faire une caractérisation à difféomorphisme près est ouverte ; la réponse est en tout cas positive en dimension 4[14]. On dispose également d'un théorème de classification complet pour l'hypothèse de positivité au sens large[15].

L'introduction de la notion de courbure isotrope à l'occasion de l'article de Micallef et Moore et de la condition de positivité associée[13] s'est révélée fructueuse, particulièrement dans les années 2000. La condition peut être formulée sur le tenseur de courbure : les composantes dans une base orthonormale ${\displaystyle (e_{1},e_{2},e_{3},e_{4})}$ vérifient

${\displaystyle R_{1313}+R_{1414}+R_{2323}+R_{2424}-2R_{1234}\geq 0\qquad (>0).}$

Cette condition prend en fait son origine dans l'analyse de l'opérateur de courbure sur les complexifiés des espaces tangents : la condition de positivité n'est exigée que sur les 2-plans isotropes pour la structure hermitienne de ce complexifié. La condition de courbure isotrope positive n'est ni plus ni moins exigeante que la courbure sectionnelle positive, mais elle se révèle avoir de bonnes propriétés, notamment le fait d'être une condition stable lors de l'évolution de la métrique par le flot de Ricci[16]

• (en) Marcel Berger, A Panoramic View of Riemannian Geometry, 2003 [détail de l’édition]
• (en) Burkhard Wilking, « Nonnegatively and Positively curved manifolds », Journal of Differential Geometry,‎ 2007 (lire en ligne)

• Théorème de Synge
• Théorème de l'âme
• Théorème de Bonnet-Schoenberg-Myers
• Courbure négative