Convergence faible (espace de Hilbert)

En mathématiques, la convergence faible dans un espace de Hilbert est la convergence d'une suite de points dans la topologie faible.

Définition

Une suite de points $(x_{n})$ dans un espace de Hilbert H converge faiblement vers un point $x$ dans H si

\langle x_{n},y\rangle \to \langle x,y\rangle

pour tout $y$ dans H, $\langle \cdot ,\cdot \rangle$ désignant le produit scalaire de l'espace de Hilbert.

La notation

x_{n}\rightharpoonup x

est parfois utilisée pour désigner ce type de convergence.

Exemples

Convergence faible des suites orthonormales

Considérons une suite $(e_{n})$ orthonormée, c'est-à-dire

\langle e_{n},e_{m}\rangle =

δ mn

Si cette suite est infinie, alors elle converge faiblement vers zéro.

Démonstration

Pour $x$ ∈ H, on a

\sum _{n}|\langle e_{n},x\rangle |^{2}\leq \|x\|^{2}

(Inégalité de Bessel)

où l'égalité est vraie lorsque ${\textstyle (e_{n})}$ est une base d'espace de Hilbert. Donc

|\langle e_{n},x\rangle |^{2}\to 0

(puisque la série ci-dessus converge, son terme général tend vers zéro)

c.-à-d.

\langle e_{n},x\rangle \to 0

Lemme de Riemann-Lebesgue

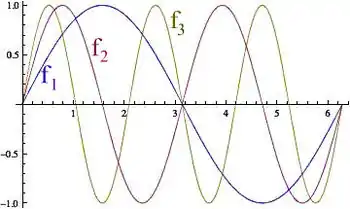
The first 3 curves in the sequence fn=sin(nx)

Les 3 premières fonctions de la suite

f_{n}(x)=\sin(nx)

sur

[0,2\pi ]

. Quand

n\to \infty

f_{n}

converge faiblement vers

f=0

L'espace de Hilbert $L^{2}[0,2\pi ]$ est l'espace des fonctions de carré intégrable sur l'intervalle $[0,2\pi ]$ muni du produit scalaire défini par

\langle f,g\rangle =\int _{0}^{2\pi }f(x)\,{\overline {g(x)}}\;\mathrm {d} x

(voir espace L²). La suite de fonctions $(f_{n})_{n\in \mathbb {N} }$ définie par

f_{n}(x)=\operatorname {e} ^{\mathrm {i} nx}

converge faiblement vers la fonction nulle dans $L^{2}[0,2\pi ]$ , puisque pour toute fonction $g\in L^{2}[0,2\pi ]$ , l'intégrale

\langle f_{n},g\rangle =\int _{0}^{2\pi }\operatorname {e} ^{\mathrm {i} nx}\,{\overline {g(x)}}\;\mathrm {d} x

tend vers $\langle 0,g\rangle =0$ quand $n$ tend vers l'infini : c'est un cas particulier à la fois de l'exemple précédent et du lemme de Riemann-Lebesgue.

On peut remarquer que $f_{n}$ ne converge pas vers 0 en norme $\|\cdot \|_{\infty }$ ou $\|\cdot \|_{2}$ . Cette non-convergence est l'une des raisons pour lesquelles ce type de convergence est considéré comme « faible ».

Propriétés

Si une suite converge fortement, elle converge également faiblement.
Dans un espace de Hilbert (comme dans tout espace réflexif) les boules fermées sont faiblement compactes, donc toute suite bornée possède une sous-suite faiblement convergente. Notez que les ensembles fermés et bornés ne sont généralement pas faiblement compacts dans les espaces de Hilbert (par exemple, l'ensemble constitué d'une suite orthonormée comme ci-dessus est fermé et borné mais pas faiblement compact car il ne contient pas 0). Cependant, les ensembles bornés et faiblement fermés sont faiblement compacts, de sorte que chaque ensemble fermé convexe borné est faiblement compact.
Comme dans tout e.v.n., toute suite faiblement convergente est bornée.
La norme est (séquentiellement) faiblement semi-continue inférieurement : si $x_{n}$ converge faiblement vers $x$ , alors
$\Vert x\Vert \leq \liminf _{n\to \infty }\Vert x_{n}\Vert ,$

et cette inégalité est stricte chaque fois que la convergence n'est pas forte. Par exemple, toute suite orthonormale infinie converge faiblement vers zéro (voir supra).
Si $x_{n}$ converge faiblement vers $x$ et si l'hypothèse supplémentaire $\lVert x_{n}\rVert \to \lVert x\rVert$ est vérifiée, alors $x_{n}$ converge vers $x$ fortement car
$\langle x-x_{n},x-x_{n}\rangle =\langle x,x\rangle +\langle x_{n},x_{n}\rangle -\langle x_{n},x\rangle -\langle x,x_{n}\rangle \to 0$ .
Sur un espace de Hilbert de dimension finie, c'est-à-dire un espace euclidien ou hermitien, les topologies faible et forte coïncident.
Les espaces de Hilbert possèdent la propriété de Banach-Saks : pour toute suite bornée $(x_{n})$ , il existe une sous-suite $(x_{n_{k}})$ dont la suite des moyennes de Cesàro converge fortement.

Généralisation

La définition de convergence faible peut être étendue aux espaces de Banach. Une suite de points $(x_{n})$ dans un espace de Banach B est dite faiblement convergente vers un point $x$ dans B si

f(x_{n})\to f(x)

pour toute forme linéaire continue $f$ sur $B$ c'est-à-dire pour tout $f$ dans le dual topologique $B'$ .

Dans le cas où $B$ est un espace de Hilbert, grâce au théorème de représentation de Riesz, il existe un $y$ dans $B$ tel que

f(\cdot )=\langle \cdot ,y\rangle

ce qui permet de retrouver la définition de la convergence faible sur un espace de Hilbert.

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.