Contrainte principale
En science des matériaux, et en particulier en mécanique des milieux continus et résistance des matériaux, les contraintes principales (σI, σII, σIII) sont les contraintes exprimées dans une base telle que le tenseur des contraintes est une matrice diagonale. Cette base est orthonormée (voir Matrice symétrique, § Décomposition spectrale).
Explication
L'état de contrainte d'un élément de matière peut se représenter par un tenseur, le tenseur des contraintes. Dans une base donnée de l'espace , ce tenseur se représente par une matrice 3×3 :
- .
Si le tenseur des contraintes décrit un état à l'équilibre, alors la matrice est symétrique ; elle est par ailleurs à coefficients réels.
D'après le théorème spectral en dimension finie, cette matrice est diagonalisable ; il existe une base orthonormée pour laquelle cette matrice est une matrice diagonale[1] :
- .
Les directions sont appelées directions principales.
Par convention, on prend σI ≥ σII ≥ σIII.
La contrainte σI correspond à la contrainte de traction maximale. Si σIII < 0, alors σIII correspond à la contrainte de compression maximale. La contrainte de cisaillement maximale, celle retenue pour le critère de Tresca, correspond à
- .
Si l'on n'impose pas un ordre de contraintes décroissantes, alors
- .
Les lignes de courant des contraintes principales, c'est-à-dire les courbes qui sont tangentes aux vecteurs contrainte principale en tout point, sont appelées lignes isostatiques. Elles permettent de visualiser de quelle manière les efforts internes se répartissent dans la matière.
Résultat — La contrainte principale maximale correspond à la contrainte de traction maximale.
Si la contrainte principale minimale est négative, alors elle correspond à la contrainte de compression maximale.
La contrainte de cisaillement maximal vaut :
- .
Ceci est important lorsque l'on veut étudier les risques de rupture. En effet, l'utilisation d'une contrainte équivalente scalaire comme la contrainte de von Mises ou la contrainte de Tresca n'indique pas si une zone est soumise à de la traction, de la compression et/ou du cisaillement. Or, une contrainte de type compression est moins dangereuse car elle a tendance à refermer les fissures.
Détermination
On peut déterminer les directions et contraintes principales :
- grâce au cercle de Mohr[2] ;
- par les méthodes algébriques, en remarquant que les contraintes principales sont les valeurs propres du tenseur, et les directions principales, ses vecteurs propres.
Les valeurs propres λ vérifient l'équation
- det(T - λI) = 0
où T est le tenseur des contraintes et I la matrice identité. On peut réécrire cette équation avec les invariants du tenseur des contraintes :
- λ3 - I1λ2 + I2λ - I3 = 0.
On impose σI > σII > σIII.
Notons que, par définition de la racine d'un polynôme, on a
- (λ - σI)(λ - σII)(λ - σIII) = 0
Contraintes octaédriques
Considérons un cube dont les faces sont normales aux directions principales. Les contraintes σI, σII et σIII sont des contraintes normales aux faces de ce cube ; les contraintes tangentielles sont nulles.
Considérons maintenant l'octaèdre dont les sommets sont les centres des faces du cube. Pour chaque face, on a :
- une contrainte normale σoct ;
- une contrainte tangentielle τoct.
Ces contraintes sont appelées contraintes octaédriques.
Les contraintes normales et tangentielles sur les huit faces de l'octaèdre sont identiques, et valent[3] :
- ;
- .
Notons que par rapport à la pression isostatique P et à la contrainte équivalente de von Mises σe, on a :
- ;
- .
Le terme « contrainte normale octaédrique » est parfois utilisé comme synonyme de « pression isostatique ».
La contrainte normale octaédrique σoct tend à faire varier le volume de l'octaèdre sans le gauchir (sans faire varier les angles). À l'inverse, la cission octaédrique tend à distordre l'octaèdre sans faire varier son volume ; on retrouve donc logiquement un rapport avec la contrainte de von Mises.
Cas particuliers
État de contrainte uniaxiale
Dans le cas de la sollicitation uniaxiale, deux des contraintes principales sont nulles. On choisit par convention σI ≠ 0 ; xI est l'axe de traction, on a |σI| = F/S (la contrainte nominale), σII = σIII = 0. Le tenseur des contraintes principales s'écrit donc
Dans le cas de la compression unixiale, on a σI < 0, donc σI < σII et σI < σIII contrairement à la convention initiale. On a dans tous les cas τmax = ½|σI|.
État de contraintes planes
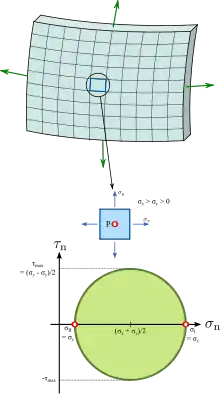
Dans le cas de contraintes planes, une des contraintes principales est nulle. On choisit arbitrairement σIII = 0 ; on peut alors avoir σII < 0 donc σII < σIII, contrairement à la convention précédente. Dans tous les cas, on a τmax = ½|σI - σII|.
Le tenseur des contraintes principales s'écrit donc
Pression isostatique pure
Dans le cas d'une pression isostatique P, on a σI = σII = σIII = P. Le tenseur des contraintes principales s'écrit
et τmax = 0.
Utilisation
Dans cette base, les lois s'expriment de manière plus simple. En particulier, les contraintes principales permettent d'établir le critère de plasticité ou de ruine, par exemple en considérant la cission maximale (critère de Tresca). La connaissance des directions principales permet
- de savoir comment orienter une jauge de contrainte ;
- de prédire la progression des fissures ; en particulier, en fatigue : dans les métaux, des microfissures apparaissent dans le plan de cission maximal (stade I), puis une fissure se crée et se propage dans le plan de tension maximal (stade II).
Notes et références
- Fanchon 2001, p. 437
- Fanchon 2001, p. 438-440
- Fanchon 2001, p. 441-442












