Compression gravitationnelle
La compression gravitationnelle est le phénomène dans lequel la gravité, agissant sur la masse d'un objet, compresse celui-ci, réduisant son volume et augmentant sa densité et sa température.
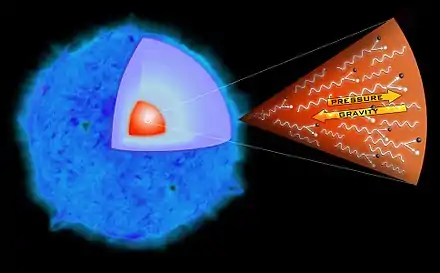
Ainsi, au centre d'une planète ou d'une étoile, la compression gravitationnelle produit de la chaleur par le mécanisme de Kelvin-Helmholtz. Ce mécanisme explique comment, par exemple, Jupiter continue d'émaner une chaleur produite par sa compression gravitationnelle[2].
Évolution stellaire
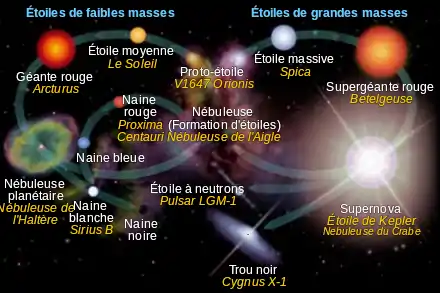
On réfère plus communément à la compression gravitationnelle dans le domaine de l'évolution stellaire. Ainsi, au niveau de la naissance des étoiles, le Soleil et les autres étoiles de la séquence principale sont produites par l'effondrement gravitationnel d'un nuage moléculaire.
En supposant la masse assez grande, la compression gravitationnelle réduit la grosseur du noyau de l'astre produit, engendrant une augmentation de sa température jusqu'à l'obtention d'un commencement de fusion nucléaire. Les processus de fusion de l'hydrogène vers l'hélium produisent une énergie qui équilibre la pression gravitationnelle vers l’intérieur, stabilisant ainsi l'étoile pour des millions ou des milliards d'années selon sa masse.
Aucune compression gravitationnelle supplémentaire n'intervient jusqu'au moment où l'hydrogène est presque complètement utilisé, réduisant ainsi la pression thermique de la réaction de fusion[3] et amenant, dans un premier temps, une nouvelle compression. L'augmentation de densité et de température de cette dernière, conjuguée à l'accumulation d'hélium, entraîne la fusion de l'hélium, ce qui augmente fortement la pression thermique et mène l'étoile au stade de géante rouge.
Une fois terminée la fusion de l'hélium, il y a chute de la pression thermique, ce qui amène la matière à être compressée jusqu'à ce qu'un nouvel équilibre soit atteint. Ce dernier dépend de la masse de l'étoile.

Cadavres stellaires


Si l'étoile possède une masse semblable à celle du Soleil, les montées de température et de densité sont insuffisantes pour engendrer d'autres processus de fusion nucléaire. Une partie de la matière est éjectée et forme une nébuleuse planétaire, alors que la matière qui reste est compressée jusqu'à ce que la gravité soit compensée par la pression de dégénérescence, ce qui mène à la formation d'une naine blanche[4].
Les étoiles plus massives que le Soleil évoluent différemment. Elle brûlent leur combustible très rapidement et vivent beaucoup moins longtemps. Après la fusion de l'hélium, elles entament d'autres processus de fusion nucléaire et se rendent jusqu'à la fusion du fer. À ce moment, il n'est plus possible de soutirer de l'énergie par fusion. La pression thermique disparaît et l'étoile s'effondre, menant d'abord à une supernova, qui éjecte une partie de la matière, puis à la compression de la matière restante en une étoile à neutrons[5] ou un trou noir[6]. L'un ou l'autre dépend, encore une fois, de la masse de l'astre.
Si la masse de ce qui reste de l'étoile dépasse la masse de Chandrasekhar, l'effet de compression gravitationnelle sera assez fort pour faire entrer en contact les protons et les électrons des atomes qui forment le noyau de l'étoile (principalement du nickel 56) pour les fusionner en neutrons.
Si la masse résiduelle est plus élevée, le cadavre stellaire prend la forme d'un noyau de fer 56 d'une masse supérieure à la limite d'Oppenheimer-Volkoff, soit environ entre 2,4 et 3,2 masses solaires[7]. Lorsqu’une telle masse est atteinte, même les neutrons ne sont plus en mesure de conserver leur état et rien ne peut équilibrer la compression gravitationnelle. Toute la matière est alors condensée en une singularité gravitationnelle au centre de l'étoile et devient un trou noir.
| Limite de Chandrasekhar | Masse de l'étoile | Type d'étoile |
|---|---|---|
| inférieur | entre 0,8 et 1,4 masse solaire | naine blanche |
| supérieur | Entre 2 et 5-6 masses solaires | étoile à neutrons |
| supérieur | 8 masses solaires | trou noir |
Différenciation planétaire
La compression gravitationnelle mène à la différenciation planétaire.
Théorème du viriel
Le théorème du viriel est une relation générale qui s'applique à un système de plusieurs corps en interaction[8]. Il peut être utilisé en astrophysique pour expliquer l'équilibre dynamique entre la gravité et les sources internes de fusion de l'étoile[9].
Tel qu'énoncé à l'origine par Rudolf Clausius, le théorème s'applique à un ensemble stable de particules de masse repérées par leurs positions et leurs vitesses , sur lesquelles s'exercent des forces [10]. Il s'écrit :
où la barre de surlignement désigne la moyenne temporelle des quantités correspondantes.
Notes et références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Gravitational compression » (voir la liste des auteurs).
- (en) « Chandra X-ray Observatory », Chandra X-ray Center, Operated for NASA by the Smithsonian Astrophysical Observatory, (consulté le )
- (en) « Jupiter », Space Research Institute,Russian Academy of Sciences (consulté le )
- (en) R.R. Britt, « How a Star is Born: Clouds Lift on Missing Link », (consulté le )
- (en)(en) « White Dwarf Stars », Astrophysics Science Division, NASA Goddard Space Flight Center., (consulté le )
- (en)(en) M. Coleman Miller, « Introduction to neutron stars », University of Maryland (consulté le )
- (en)(en) N. Strobel, « Black Holes », Nick Strobel's Astronomy Notes, (consulté le )
- (fr)(en) M. Loic Villain, « Trou noir, dossier introductif », Futura-Sciences (consulté le )
- Daniel FARQUET, « Théorème du viriel »
- (en) Chandrasekhar S, An Introduction to the Study of Stellar Structure, Chicago, University of Chicago Press, , p. 49–53
- Théorème du viriel




