Arbre de jeu
En théorie des jeux, un arbre de jeu est un arbre (au sens de la théorie des graphes) dont les nœuds sont des positions dans un jeu et dont les arêtes sont des mouvements. L'arbre de jeu complet est l'arbre de jeu commençant à la position initiale et contenant tous les mouvements possibles depuis chaque position.
Arborescence
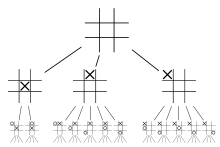
Le diagramme ci-contre montre comment coder dans une représentation arborescente le premier tour de jeu au tic-tac-toe : ce sont les deux premiers niveaux dans l'arborescence, la racine représentant la position initiale (une grille vide, en l'occurrence). Les rotations et les réflexions de la grille sont équivalentes, le premier joueur a donc trois choix de déplacement: au centre, au milieu d'un bord ou dans un coin. Le deuxième joueur a deux choix pour la réponse si le premier joueur a joué au centre, sinon cinq choix, ainsi de suite.
Le nombre de feuilles dans l'arbre complet du jeu correspond au nombre de parties différentes possibles de jouer au jeu. Par exemple, l'arborescence du tic-tac-toe comporte 255 168 feuilles.
Les arbres de jeu sont importants dans le domaine de l'intelligence artificielle, car une façon de choisir le meilleur coup dans un jeu est de rechercher dans l'arbre du jeu en utilisant l'un des nombreux algorithmes de parcours d'arbre, combinés à des règles de type minimax pour élaguer l'arbre . Le parcours de l'arbre du tic-tac-toe est relativement simple, mais pour des jeux où le nombre de coups possibles est important, comme aux échecs, l'arbre complet du jeu est beaucoup trop grand pour être parcouru. Pour parer à cela un programme de jeu d'échecs recherche un arbre de jeu partiel: le programme parcourt le plus de niveaux possibles depuis la position actuelle dans le temps dont il dispose. Hormis le cas des arbres de jeu «pathologiques»[1] (qui semblent assez rares en pratique), augmenter la profondeur de recherche (c'est-à-dire le nombre de plis recherchés) améliore généralement les chances de choisir le meilleur coup.
Les jeux à deux peuvent également être représentés sous forme d'arbres et/ou. Pour que le premier joueur gagne une partie, il doit exister un coup gagnant pour tous les coups du deuxième joueur. Ceci est représenté dans l'arbre et/ou en utilisant la disjonction pour représenter les mouvements alternatifs du premier joueur et en utilisant la conjonction pour représenter tous les mouvements du deuxième joueur.
Résolution des arbres de jeu
Algorithme déterministe
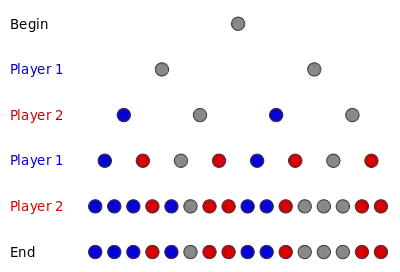
Avec un arbre de jeu complet, il est possible de «résoudre» le jeu, c'est-à-dire de trouver une séquence de coups que le premier ou le deuxième joueur peut suivre et qui garantira le meilleur résultat possible pour ce joueur (généralement une victoire ou une égalité). L'algorithme (qui est généralement appelé raisonnement rétrograde ou analyse rétrograde) peut être décrit de manière récursive comme suit, en partant d'un arbre de jeu complet non coloré :
- Colorez le dernier niveau de l'arbre de jeu de sorte que toutes les victoires du joueur 1 soient colorées dans un sens (bleu dans le diagramme), toutes les victoires du joueur 2 soient colorées d'une autre façon (rouge dans le diagramme) et toutes les égalités soient colorées d'une troisième façon (gris sur le diagramme).
- Remontez aux nœuds du niveau supérieur. Si l'un des fils d'un nœud est de couleur opposée au joueur actuel, colorez le nœud de la couleur de ce fils. Si tous les fils d'un nœud sont de la même couleur que le joueur actuel, colorez ce nœud de la même couleur. Sinon, colorez ce nœud avec une égalité.
- Répétez l'étape 2, en vous déplaçant vers le haut, jusqu'à ce que tous les nœuds soient colorés. La couleur du nœud racine déterminera la nature du jeu.
Il est généralement possible de résoudre un jeu (dans ce sens technique de «résoudre») en utilisant uniquement un sous-ensemble de l'arbre de jeu, car dans de nombreux jeux, un mouvement n'a pas besoin d'être analysé s'il y a un autre mouvement qui est meilleur pour le même joueur. C'est le principe utilisé pour l'élagage alpha-bêta qui peut être utilisé dans de nombreux jeux déterministes.
Tout sous-arbre pouvant être utilisé pour résoudre le jeu est connu sous le nom d'arbre de décision, et la taille des arbres de décision de différentes formes est utilisée comme mesure de la complexité du jeu[2].
Algorithmes probabilistes
Un autre moyen pour résoudre les arbres de jeu est l’utilisation d'algorithmes randomisés. Cette méthode présente deux avantages important: la rapidité et la praticité. Alors qu'une version déterministe de la résolution des arbres de jeu peut être effectuée en Ο(n), l'algorithme aléatoire suivant a un temps d'exécution attendu de θ(n0.792) si chaque nœud de l'arbre de jeu a le degré 2. Son côté pratique vient du fait qu'un adversaire ne peut pas battre le système d'arbres de jeu en connaissant l'algorithme utilisé pour résoudre l'arbre de jeu car l'ordre de résolution est aléatoire.
L'algorithme suivant est une version possible de résolution d'arbre de jeu de façon aléatoire[3]:
def gt_eval_rand(u) -> bool:
"""Renvoie True si ce noeud est évalué en victoire, sinon renvoie False"""
if u.leaf:
return u.win
else:
random_children = (gt_eval_rand(child) for child in random_order(u.children))
if u.op == "OR":
return any(random_children)
if u.op == "AND":
return all(random_children)
L'algorithme utilise l'idée de "court-circuit": Dans le cas où la racine est considéré comme un "OR "opérateur, elle est classée comme True si un True est trouvé dans l'arbre; inversement, dans le cas où la racine est considéré comme un "AND "opérateur, elle est classée comme False si un False est trouvé dans l'arbre.
Articles connexes
- Élagage alpha-bêta
- Jeu de forme complet
- Nombre de Shannon
- Complexité du jeu
Annexes
- Te Chiang Hu et Shing, Man-tak, Combinatorial Algorithms, Courier Dover Publications, (ISBN 0-486-41962-2, lire en ligne)
- Judea Pearl, Heuristique, Addison-Wesley, 1984
Notes et références
- (en) Nau, « An investigation of the causes of pathology in games », Artificial Intelligence, vol. 19, , p. 257–278 (DOI 10.1016/0004-3702(82)90002-9)
- Victor Allis, Searching for Solutions in Games and Artificial Intelligence, Ph.D. Thesis, University of Limburg, Maastricht, The Netherlands, (ISBN 90-90-07488-0, lire en ligne)
- Daniel Roche, SI486D : Randomness in Computing, Game Trees Unit, United States Naval Academy, Computer Science Department, (lire en ligne)