Raisonnement rétrograde
Le raisonnement rétrograde ou l'induction à rebours (Backward induction) est une méthode de raisonnement qui consiste à partir d'un résultat final connu pour retracer les étapes ou les événements qui ont conduit à ce résultat.
Principalement utilisée en théorie des jeux, il est utilisé pour résoudre les jeux de manière séquentielle en partant de la fin du jeu et en remontant jusqu'au début. Cela consiste à considérer les actions des joueurs à chaque étape en se basant sur ce qui se passerait à l'étape suivante, puis en remontant jusqu'à l'étape initiale.
Il est mentionné pour la première fois par John von Neumann et Oskar Morgenstern dans leur ouvrage Theory of Games and Economic Behavior (Théorie des jeux et du comportement économique) publié en 1944.
Exemple d'application
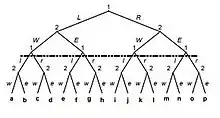
Dans le cadre de la recherche d'un optimum, le raisonnement par induction implique qu'un nœud - c'est-à-dire une décision à prendre entre plusieurs options - qui comporte des sous-nœuds ne peut être résolu qu'en ayant résolu chacun des sous-nœuds.
A
/ \
/ \
A1 A2
/ \ / \
A11 A12 A21 A22
(3) (2) (1) (4) (bénéfice)
- en fonction des bénéfices, on peut choisir la meilleure option entre A11 et A12 : le nœud A1 sera alors assimilé à A11
- de la même manière, A2 sera assimilé A22
- le raisonnement par induction s'applique ensuite entre A1 et A2. A sera assimilé à la meilleure option d'entre ces deux nœud, c'est à dire A2
Le raisonnement rétrograde permet de résoudre de nombreux problèmes simples, dans la mesure où les coefficients (bénéfices) et la structure du jeu (arbre) sont connus, constants et délimités.