Algorithme de Karplus-Strong

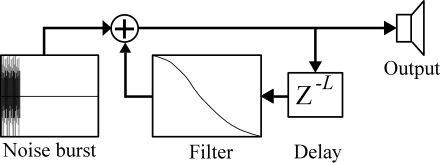
L'implémentation électronique de Karplus-Strong, telle que décrite en figure 2, page 45 de la publication originale au sein du Computer Music Journal[1] est illustrée par le schéma ci-dessus.

1. Tout d'abord, un extrait sonore de taille fixée (${\displaystyle L}$ échantillons discrets, correspondant à une seule forme d'onde dans le domaine temporel, et donc à une longueur d'onde à la fréquence fondamentale voulue) est envoyée dans le système. Dans l'implémentation initiale, il s'agit de bruit blanc, mais cela n'empêche pas l'emploi d'une autre forme d'onde comme un signal en dents de scie filtré ou non pour obtenir des résultats à la texture sensiblement différente.
2. Cet extrait sonore, en plus d'être envoyé vers la sortie sonore principale, est simultanément envoyé vers une ligne de délai ayant un délai correspond à la taille de la forme d'onde (${\displaystyle L}$ échantillons), et qui produira donc une sortie une fois que la première forme d'onde aura été jouée.
3. Un filtre passe-bas très basique est appliqué sur la sortie cette première ligne de délai. Il est implémenté, dans la publication initiale, par l'application d'une moyenne entre chaque échantillon de la forme d'onde et la précédente (cette moyenne impliquant l'utilisation d'une seconde ligne de délai d'une longueur d'un échantillon).
4. Une sortie audio provenant de l'extrait sonore initial, le temps de première forme d'onde (elle est alors constituée de forme d'onde originale, avec toutes ses harmoniques, jouée une seule fois), puis du filtre passe-bas vers lequel est réinjecté cycliquement le signal modifié est produite.

Pour comprendre comment fonctionne le filtre passe-bas simple suggéré par l'article de recherche, il faut comprendre les effets de l'opération de moyenne utilisée. Puisque cette perte de résolution est effectuée sur des échantillons adjacents, les plus hautes fréquences sont d'abord touchées et davantage que les basses, et puisque chaque valeur est transformée en une moyenne entre elle-même et la précédente, l'amplitude totale de la forme d'onde finit forcément par décroître. Cela reflète l'amortissement de la résonance.

En plus de l'algorithme de génération de cordes pincées mentionné ci-dessus, l'article de recherche fait mention, en pages 46 à 47 du journal de publication, d'un algorithme de génération de sons de batteries.

De base, son principe consiste, pour une fraction répartie aléatoirement correspondant à 50 % des échantillons produits, à inverser le signe de l'échantillon après l'opération de moyenne[1].

De fait, l'effet de filtre fréquentiel est perdu et le son produit, apériodique, se rapproche d'un simple extrait de bruit irrégulier avec un fondu en fermeture[2].

Le principe de l'algorithme de Karplus-Strong sert de base à de nombreux synthétiseurs, virtuels ou non. Le générateur « Pluck » (cordes pincées) du logiciel Audacity est basé sur son principe, d'après les déclarations des développeurs[3].

Ci-dessous se trouve un exemple d'implémentation basique de l'algorithme en langage Python.

#!/usr/bin/python3
#-*- encoding: Utf-8 -*-
from numpy import array as np_array
from scipy.io.wavfile import write
from sounddevice import play
from random import random
from typing import List
# Install dependencies:
# sudo pip3 install --upgrade scipy sounddevice numpy
# All frequencies used below are expressed in Hertz
def karplus_strong(
    noise_samples : List[int],
    number_output_samples : int
):
    output_samples : List[int] = []
    for wavetable_iteration in range(number_output_samples // len(noise_samples)):
        for output_position in range(len(noise_samples)):
            wavetable_position = output_position % len(noise_samples)
            # Apply the (very simple) low-pass filter = mean over adjacent PCM
            # samples values over each sample
            noise_samples[wavetable_position] = (
                noise_samples[wavetable_position] +
                noise_samples[(wavetable_position - 1) % len(noise_samples)]
            ) / 2
        # Copy the next iteration of filtered waveform into the output
        output_samples += noise_samples
    return np_array(output_samples)
def do_karplus_strong_with_noise(
    output_length_seconds : float,
    fundamental_frequency : int
) -> None:
    work_sampling_frequency = 8000
    resampled_sampling_frequency = int(8000 * (2.0 / output_length_seconds))
    # Calculate the length in samples of a single wavelength
    wavelength_in_samples = int(round(
        (work_sampling_frequency / fundamental_frequency) *
        (resampled_sampling_frequency / work_sampling_frequency)
    ))
    # Generated random samples in the range [-1.0;1.0]; as expected by Numpy
    noise_samples : List[float] = [random() * 2 - 1 for i in range(wavelength_in_samples)]
    # Apply the Karplus-Strong plucked string algorithm over the noisey waveform
    pluck_samples : List[float] = karplus_strong(
        list(noise_samples),
        work_sampling_frequency * 2 # Apply the algorithm to 2 seconds of sample at 8000 Hz
    )
    # Play the output sound
    play(pluck_samples, blocking = True, samplerate = resampled_sampling_frequency)
    # In addition, save the produced sound to a file in order to enable
    # further analysis with software such as Audacity
    write('output_file.wav', resampled_sampling_frequency, pluck_samples)
do_karplus_strong_with_noise(
    output_length_seconds = 0.363,
    fundamental_frequency = 303
)

Dans un langage de bas niveau, l'implémentation de l'algorithme est économe puisque l'opération de moyenne constituant le filtre passe-bas peut être implémentée avec une division et un décalage d'un bit vers la droite (équivalent d'une division par deux)[4]. À l'époque de la suggestion, en 1983, cela permet la synthèse en temps réel avec les processeurs de l'époque Intel 8080A, Texas Instruments TMS9900 (en) et SC/MP[5].

Plusieurs implémentations de référence en C++ de l'algorithme de synthèse de cordes pincées, ainsi que d'autres algorithmes dérivés de Karplus-Strong et notamment de type guide d'ondes numérique (en) sont présentes dans le STK (Sound Toolkit) édité par le CCRMA de l'université Stanford, publié sous licence libre[6].

Illustration d'un spectrogramme (ou sonogramme) d'une vibration produite avec l'algorithme de Karplus-Strong, généré avec Audacity par une transformation de Fourier glissante : on observe globalement l'absence de représentation des fréquences inharmoniques (leur présence vers le début est due à un détail de fonctionnement de la transformation utilisée) et le déclin progressif des différentes harmoniques, les plus hautes en premier.

Dans l'algorithme de synthèse de sons de cordes pincées (algorithme de Strong inventé en décembre 1978), illustré ci-dessus, il peut être observé que le déclin d'une harmonique s'étale sur une durée approximativement proportionnelle au nombre d'échantillons d'une seule forme d'onde au cube, divisé par le numéro de l'harmonique en question au carré[7]. Une analyse mathématique plus détaillée est proposée par le papier de recherche, proposant notamment un calcul exact qui dépend de paramètres trigonométriques et est mis en relation avec le principe de transformée en Z, lui-même sous-jacent au plus classique filtre en peigne[8].

Plus prosaïquement, les corollaires de base qui permettent le fonctionnement de l'algorithme peuvent être expliquées expérimentalement comme il suit :

1. Le fait de répéter cycliquement une forme d'onde aléatoire de taille courte suffit à créer un motif périodique, faisant apparaître à l'intervalle de la forme d'onde et à toutes ses harmoniques du contenu fréquentiel.
2. Le fait que des harmoniques, de différentes intensités, soient présentes dans la forme d'onde initiale est dû au caractère apériodique de la forme d'onde choisie.
3. Le lissage de la forme d'onde en remplaçant les valeurs discrètes par des moyennes contribue à la baisse progressive de la présence d'harmoniques au sein du signal, et donc de la présence de contenu fréquentiel audible (dans le domaine temporel, on tend vers un signal continu qui n'est pas audible ; l'amplitude moyenne décroît progressivement autour d'une intensité qui n'est pas 0).
4. La première passe de l'algorithme ayant d'abord un effet sur les échantillons adjacents entre eux, et induira donc d'abord une perte de résolution au niveau des éventuelles harmoniques proches de la fréquence de Nyquist ; ce sera par effet boule de neige que, progressivement, le signal sera de plus en plus lisse puisque des intervalles de plus en plus grandes seront touchées par des moyennes entre échantillons éloignés.

La longueur du déclin, de même que la fréquence de base du son produit, peuvent être modulées par un rééchantillonnage ainsi que par un changement de la longueur d'onde correspondant à la fréquence de base. Le papier évoque également la possibilité de remplacer une partie des opérations de moyenne par des opérations de copie sans modification afin de l'« étendre », ce qui tend à modifier l'aspect du son[9].

• Synthèse par modélisation physique
• Instrument à cordes pincées
• Résonance acoustique