Algorithme d'Edmonds pour les couplages
En informatique, plus précisément en théorie des graphes, l'algorithme d'Edmonds pour les couplages (blossom algorithm en anglais), aussi connu sous le nom d'algorithme des fleurs et des pétales[1] est un algorithme pour construire des couplages maximaux sur les graphes. L'algorithme a été développé par Jack Edmonds en 1961[2], et publié en 1965[3]. Étant donné un graphe quelconque G = (V, E), l'algorithme trouve un couplage M tel que chaque sommet de V est incident à au plus une arête dans E et M est de cardinal maximal. Le couplage est construit en améliorant itérativement un couplage vide initial le long de chemins augmentant dans le graphe. Contrairement au couplage biparti, ce couplage se base sur l'idée qu'un cycle de longueur impaire dans le graphe (fleur) est contracté en un seul sommet, la recherche se poursuivant de manière itérative dans le graphe contracté.
L'algorithme a une complexité temporelle en , où est le nombre d'arêtes du graphe et est son nombre de sommets. L'algorithme de Micali et Vazirani permet de résoudre le même problème en , cependant il est beaucoup plus compliqué[4].
Le blossom algorithm est historiquement important car il a donné la première preuve qu'un couplage maximal pouvait être trouvé en un temps polynomial, ce qui prouve que le problème de couplage maximal est dans la classe de complexité P.
Chemins augmentant
Étant donné G = (V, E) et un couplage M de G, un sommet v est couplé, apparié, ou couvert par M s'il existe une arête de M incidente à v.
Un chemin en G est un chemin alternant, s'il passe alternativement par des arêtes de M et des arêtes de E \ M.
Un chemin augmentant P est un chemin alternant qui commence et se termine par deux sommets non couverts par M distincts. Notez que le nombre d'arêtes de E \ M dans un chemin augmentant est supérieur de un au nombre d'arêtes de M, et par conséquent, le nombre total d'arêtes dans un chemin augmentant est impair.
Une augmentation de couplage le long d'un chemin augmentant P est l'opération consistant à remplacer M par un nouveau couplage ? .
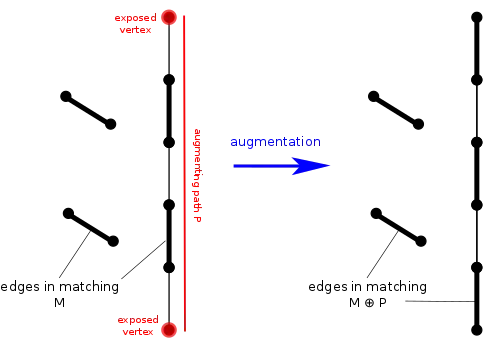
D'après le lemme de Berge, le couplage M est maximal si et seulement s'il n'y a pas de chemin augmentant de M dans G.[5] - [6] Par conséquent, soit un couplage est maximal, soit il peut être augmenté. Ainsi, à partir d'un couplage initial, nous pouvons calculer un couplage maximal en augmentant le couplage actuel avec des chemins augmentant tant que nous pouvons en trouver, et renvoyer le résultat obtenu s'il ne reste plus de chemins augmentant. Nous pouvons formaliser l'algorithme comme suit :
ENTRÉE: Graphe G, couplage initial M sur G SORTIE: couplage maximal M* sur G A1 fonction find_maximum_matching (G, M) : M* A2 P ← find_augmenting_path (G, M) A3 si P est non vide alors A4 renvoyer find_maximum_matching (G, augmentation de M le long de P) A5 sinon A6 renvoyer M A7 fin si
Nous devons encore décrire comment trouver efficacement des chemins augmentant. Le sous-programme qui réalise cette tâche utilise des fleurs et des contractions.
Fleurs et contractions
Étant donné un graphe G = (V, E) et un couplage M de G, une fleur B est un cycle dans G constitué de 2k + 1 arêtes dont exactement k appartiennent à M. En outre, une fleur comporte un sommet v (sa base) tel qu'il existe un chemin alternant de longueur paire (la tige ) de v à un sommet w non couvert par M.
Trouver des fleurs:
- Parcourez le graphe à partir d'un sommet non couvert par M.
- Étiquetez ce sommet comme un sommet externe "e".
- En commençant par ce sommet, alternez l'étiquetage entre les sommets intérieurs "i" et extérieurs "e" de sorte qu'aucun sommet adjacent ne possède le même libellé.
- Si nous nous retrouvons avec deux sommets adjacents étiquetés comme "e" externes, alors nous avons un cycle de longueur impaire et donc une fleur.
Définissons le graphe contracté' G' comme le graphe obtenu à partir de G en contractant chaque arête de B, et définissons le couplage contracté M' comme le couplage de G correspondant à M, c'est-à-dire le couplage obtenu en retirant à M toutes les arêtes de B.
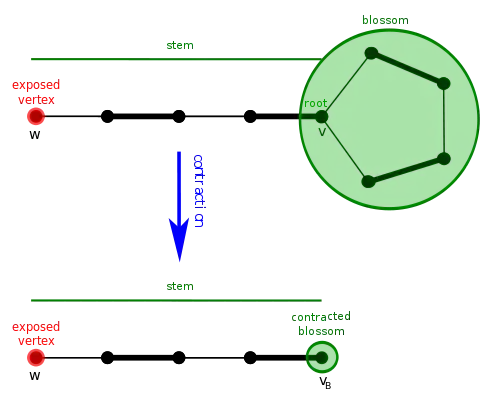
Montrons que G' a un chemin augmentant de M' si et seulement si G a un chemin augmentant de M, et que tout chemin augmentant P' de M dans G peut être étendu en un chemin augmentant de M dans G.
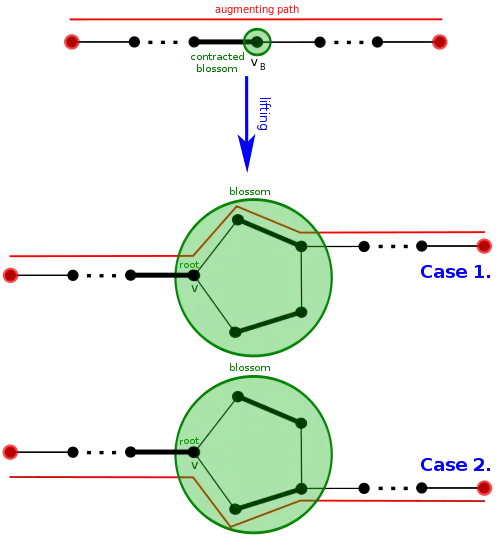
Le chemin étendu est obtenu en annulant la contraction par B du graphe G, et en intercalant dans P' les arêtes qui doivent l'être[7].
- Si P' traverse un chemin u → vB → w dans G', alors ce chemin est remplacé par le chemin u → (u'→ ... → w') → w dans G, où les sommets u' et w' de la fleur ainsi que le chemin (u'→ ... → w') dans B sont choisis pour s'assurer que le nouveau chemin est toujours alternant (u' n'est pas couvert par , ).
- si P ' a une extrémité vB, alors le chemin u → vB dans G' est remplacé par le segment u → (u '→ ... → v') dans G, où les sommets u' et v' de la fleur ainsi que le chemin (u'→ ... → v') dans B sont choisis pour s'assurer que le nouveau chemin est toujours alternant (v' n'est pas couvert par M, ).
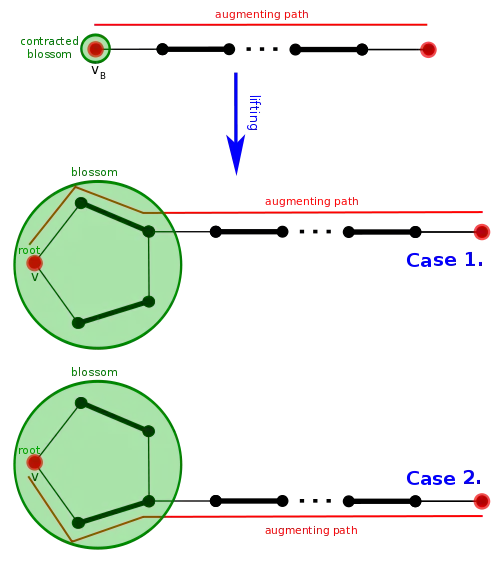
Ainsi, la recherche peut être effectuée à partir du graphe obtenu en contractant les fleurs. Cette réduction est au cœur de l'algorithme d'Edmonds.
Trouver un chemin augmentant
La recherche d'un chemin augmentant utilise une structure de données auxiliaire constituée d'une forêt F dont les arbres correspondent à des portions spécifiques du graphe G. Cette forêt F est la même que celle utilisée pour trouver un couplage maximal dans un graphe biparti (sans avoir besoin de réduire les fleurs). A chaque itération, l'algorithme soit (1) trouve un chemin augmentant, (2) trouve une fleur et s'appelle récursivement sur le graphe contracté correspondant, ou (3) conclut qu'il n'y a pas de chemin augmentant. La structure auxiliaire est construite par la procédure incrémentale décrite ci-dessous[7].
La procédure de construction considère les sommets v et les arêtes e de G et met à jour F de manière incrémentale si nécessaire. Si v est dans un arbre T de la forêt, nous noterons root(v) la racine de T. Si u et v sont tous les deux dans le même arbre T dans F, nous noterons distance(u, v) la longueur du chemin unique de u à v dans T.
ENTRÉE: un graphe G, un couplage M sur G
SORTIE: un chemin augmentant P dans G ou le chemin vide si aucun chemin augmentant n'est trouvé
B01 fonction find_augmenting_path(G, M) :
B02 F ← forêt vide
B03 retirer toutes les marques sur des sommets et arêtes de G, marquer toutes les arêtes de M
B05 pour tout sommet v non couvert par M faire
B06 créer un arbre singleton {v} et l'ajouter à F
B07 fin pour
B08 tant que qu'il y a un sommet v non marqué dans F avec distance(v, racine(v)) paire faire
B09 tant qu'il existe une arête non marquée e = {v, w} faire
B10 si w n'est pas dans F alors
// w apparaît dans M, donc on ajoute e et l'arête de M incidente à w à F
B11 x ← sommet correspondant à w dans M
B12 ajouter les arêtes {v, w} et {w, x} à l'arbre de v
B13 sinon
B14 si la distance(w, racine (w)) est impaire alors
// Ne fais rien.
B15 sinon
B16 si racine(v) ≠ racine(w) alors
// On stocke un chemin augmentant en F{e}.
B17 P ← chemin(racine(v) → ... → v ) → (w → ... → racine(w))
B18 renvoyer P
B19 sinon
// On contracte une fleur de G et on recherche un chemin dans le graphe contracté.
B20 B ← fleur formée par e et les arêtes sur le chemin v → w dans T
B21 G', M' ← contraction de G et M par B
B22 P' ← find_augmenting_path (G', M')
B23 P ← étendre P' à G
B24 renvoyer P
B25 fin si
B26 fin si
B27 fin si
B28 marquer l'arête e
B29 fin tant que
B30 marquer le sommet v
B31 fin tant que
B32 renvoyer le chemin vide
B33 Fin fonction
Exemples
Les quatre figures suivantes illustrent l'exécution de l'algorithme. Les lignes en pointillées indiquent des arêtes qui ne sont actuellement pas présentes dans la forêt.
Tout d'abord, l'algorithme traite une arête hors forêt pour provoquer l'expansion de la forêt actuelle (lignes B10 – B12).
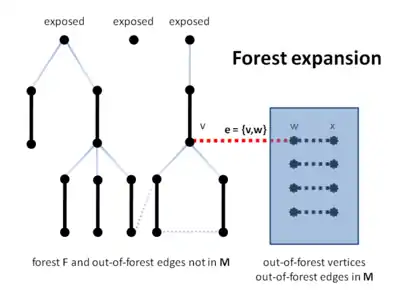
Ensuite, il détecte une fleur et contracte le graphe au niveau de cette fleur (lignes B20 – B21).
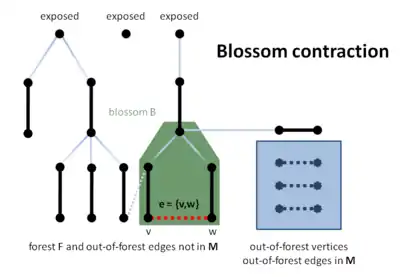
Enfin, il localise un chemin augmentant P' dans le graphe contracté (ligne B22) et le ramène au graphe d'origine (ligne B23). Notez qu'il est ici crucial que l'algorithme puisse contracter des fleurs; en effet, il ne peut pas trouver P directement dans le graphe de départ car la ligne B17 de l'algorithme ne considère que des arêtes qui n'appartiennent pas à la forêt et qui relient des sommets à distance paire des racines.
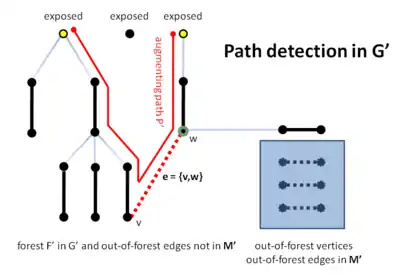
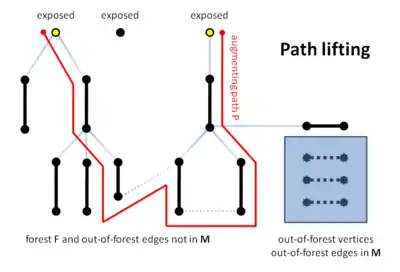
Analyse
La forêt F construite par la fonction find_augmenting_path() est une forêt alternée:
- un arbre T dans G est un arbre alterné par rapport à M, si
- T contient exactement un sommet r non couvert par M appelé racine de l'arbre
- chaque sommet à une distance impaire de la racine a exactement deux arêtes incidentes dans T,
- tous les chemins de r aux feuilles de T sont de longueur paire, leurs arêtes impaires ne sont pas dans M et leurs arêtes paires sont dans M.
- une forêt F dans G est une forêt alternée par rapport à M, si
- ses composants connexes(?) sont des arbres alternés
- chaque sommet non couvert par M dans G est une racine d'arbre alterné dans F.
Chaque itération de la boucle commençant à la ligne B09 ajoute un arbre T à F (ligne B10), ou trouve un chemin augmentant (ligne B17), ou trouve une fleur (ligne B20). Il est facile de voir que la complexité temporelle de cet algorithme est en .
Couplage biparti
Lorsque G est biparti, il n'y a pas de cycles impairs dans G. Dans ce cas, aucune fleur n'est jamais trouvée, et on peut simplement supprimer les lignes B20 – B24 de l'algorithme. L'algorithme se réduit ainsi à l'algorithme standard pour construire un couplage maximum dans un graphe biparti[6] où l'on recherche un chemin augmentant par un simple parcours de graphe : c'est par exemple le cas de l'algorithme de Ford-Fulkerson.
Couplage pondérée
Le problème du couplage maximal peut être généralisé en attribuant des poids aux arêtes dans G et en recherchant un ensemble M qui produit un couplage du poids total maximal (minimal) : c'est le problème de couplage de poids maximal. Ce problème peut être résolu par un algorithme combinatoire qui utilise l'algorithme d'Edmonds non pondéré comme sous-programme[5]. Kolmogorov en fournit une implémentation en C++ efficace[8].
Références
- Claire Mathieu, « Leçon inaugurale sur les algorithmes », sur Collège de France, .
- Edmonds, Jack (1991), "A glimpse of heaven", in J.K. Lenstra; A.H.G. Rinnooy Kan; A. Schrijver (eds.), History of Mathematical Programming --- A Collection of Personal Reminiscences, CWI, Amsterdam and North-Holland, Amsterdam, pp. 32–54
- Edmonds, Jack, « Paths, trees, and flowers », Can. J. Math., vol. 17, , p. 449–467 (DOI 10.4153/CJM-1965-045-4)
- Micali, Silvio et Vazirani, Vijay « An O(V1/2E) algorithm for finding maximum matching in general graphs » ()
—21st Annual Symposium on Foundations of Computer Science - Lovász, László et Plummer, Michael, Matching Theory, Akadémiai Kiadó, (ISBN 963-05-4168-8)
- Karp, Richard, "Edmonds's Non-Bipartite Matching Algorithm", Course Notes. U. C. Berkeley (PDF)
- Tarjan, Robert, "Sketchy Notes on Edmonds' Incredible Shrinking Blossom Algorithm for General Matching", Course Notes, Department of Computer Science, Princeton University (PDF)
- (en) Vladimir Kolmogorov, « Blossom V: a new implementation of a minimum cost perfect matching algorithm », Mathematical Programming Computation, vol. 1, no 1, 2009-07-xx, p. 43–67 (ISSN 1867-2949 et 1867-2957, DOI 10.1007/s12532-009-0002-8, lire en ligne, consulté le )








