Algorithme de Ford-Fulkerson
En informatique, l'algorithme de Ford-Fulkerson est un algorithme pour le problème de flot maximum, un problème d'optimisation classique dans le domaine de la recherche opérationnelle. Il est dû à Lester Randolph Ford junior et D. R. Fulkerson[1] et c'est une variante de l'algorithme de Busacker et Gowen.
Problème du flot maximum
Définition du problème
Ce problème d'optimisation peut être représenté par un graphe comportant une entrée (à gauche) et une sortie (à droite). Le flot représente la circulation de l'entrée vers la sortie d'où l'utilisation de cet algorithme dans les problèmes de réseaux. Les applications sont multiples : problèmes informatiques, routiers, ferroviaires, etc. Il s'applique également à tous les autres problèmes de transferts comme les importations/exportations, les flux migratoires, démographiques mais aussi sur des flux purement numériques tels que les transferts financiers. Pour les données de très grande taille, il existe plusieurs algorithmes plus performants pour résoudre le problème de flot maximum.
Exemple d'application
Une société de fret dispose de trois centres : un à Paris, le deuxième à Lyon, le troisième à Marseille. Trois destinations sont possibles : la Pologne, la Suède, la Grèce. Chacun des centres de fret a un stock initial de marchandises (Paris : 100 ; Lyon : 80 ; Marseille : 150). De même, chaque pays d'arrivée a une demande maximale pour les importations (Pologne : 120 ; Suède : 140 ; Grèce : 50).
L'algorithme de Ford-Fulkerson va permettre d'optimiser ces flux à l'aide d'un outil de modélisation mathématique. La structure sous-jacente est représentée par un graphe orienté dont le sommet de gauche symbolise le stock initial. Trois arcs en partent, chacun menant à un sommet représentant un centre de fret. Le sommet final symbolise la fin de la livraison, auquel mènent trois arcs venant de sommets représentant une destination de livraison.
Dans l'exemple présent, la matrice d'adjacence porte donc dans sa première ligne les valeurs desdits stocks. Inversement, à l'extrémité de la chaîne, la matrice associée comprendra dans sa dernière colonne les demandes respectives des pays cités. Entre les sommets « centre de fret » et les sommets « destination » peuvent se trouver des sommets et des arcs intermédiaires, les capacités de ces arcs correspondant au fret maximal d'un point à l'autre.
Paris Pologne
/ \ / \
100 --- ------- ... ------- ---- 120
/ 80 Nœuds 140 \
Départ ------- Lyon ------ intermé- ---- Suède -------- Fin
\ diaires /
150 --- ------- ... ------- ---- 50
\ / \ /
Marseille Grèce
Le problème peut être généralisé à une circulation dans un réseau (véhicules, fluides, monnaie, etc.), les grandeurs mathématiques remplaçant indistinctement les faits réels qu'elles sont censées représenter.
Réseau
Soit un réseau avec :
- un graphe orienté irréflexif ;
- une capacité avec pour convention : si l'arc n'existe pas, ;
- un sommet source s sans arcs entrants ;
- un sommet puits t sans arcs sortants.
On suppose qu'il n'y a pas d'arcs anti-parallèles, c'est-à-dire que l'existence d'un arc exclut l'existence d'un arc .
Flot
Le flot d'un réseau est une fonction qui vérifie :
- pour tous sommets , on a ;
- pour tout sommet tel que et : (le flot entrant est égal au flot sortant : propriété de conservation).
La valeur d'un flot f est .
Algorithme
Il s'agit d'un algorithme itératif. À chaque itération, la solution courante est un flot qui satisfait les contraintes de capacité (c'est donc un flot réalisable) et l'algorithme essaie d'augmenter la valeur de ce flot. Cela peut nécessiter d'annuler les mauvais choix. Pour ce faire, on définit le graphe résiduel de G et de f qui indique les modifications possibles (ajout ou annulation) : c'est un graphe pondéré où on a
et .
Pseudo-code
Entrée Un réseau Sortie Un flot maximal f Fonction Ford_Fulkerson() flot nul Tant que il y a un chemin simple de s à t dans le graphe résiduel : Pour toute arête : Si : Sinon : Renvoyer f
L'algorithme ne précise pas comment trouver chaque chemin . L'algorithme d'Edmonds-Karp, spécialisation de l'algorithme de Ford-Fulkerson, propose de faire un parcours en largeur.
Chaque chemin trouvé est garanti d’augmenter la valeur du flot, car il commence forcément par un arc sortant du sommet source et finit par un arc entrant dans le sommet puits.
Exemple d'exécution
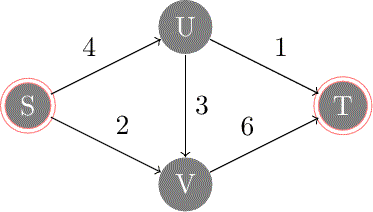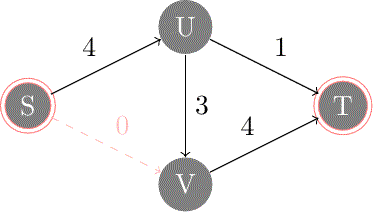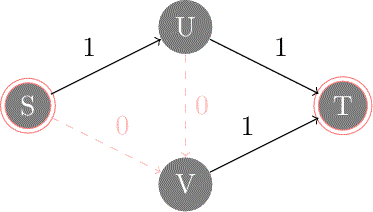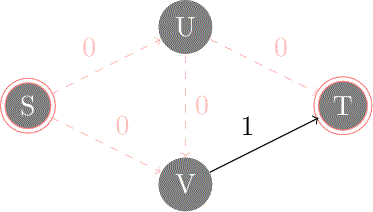
| On considère le réseau de flot , consistant du graphe à quatre sommets et cinq arêtes , de la source , du puits et de la fonction de capacité .
On commence avec le flot vide qui attribue la valeur à chaque arête. Initialement, le graphe résiduel et les capacités résiduelles correspondent alors exactement au réseau avec les capacités . |
Graphe (avec capacité ) | 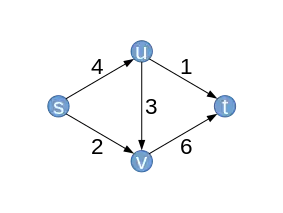 |
| |||||||||||||||||
| Flot | 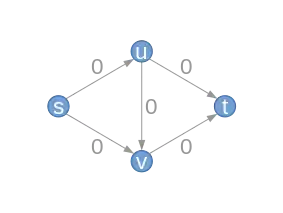 |
| ||||||||||||||||||
| Graphe résiduel (avec capacité résiduelle ) |  |
| ||||||||||||||||||
| Supposons que l'algorithme choisisse d'abord le chemin (bleu). Le long de ce chemin, on peut augmenter le débit au maximum de puisque l'arête est limitante (). Il en résulte un nouveau flot (qu'on appellera toujours ) avec .
L'arête a une capacité de . Elle est utilisée dans le flot : . Dans le graphe résiduel, sa capacité résiduelle sera donc . De même et . Les trois arêtes sont strictement positives dans le flot. Ces poids dans le flot ne sont peut être pas les plus optimaux. Les nouvelles arêtes arrières (en rouge) dans le graphe résiduel marquent alors le fait que l'on pourra toujours diminuer le flot sur ces arêtes. |
Chemin améliorant (avec capacités résiduelles ) | 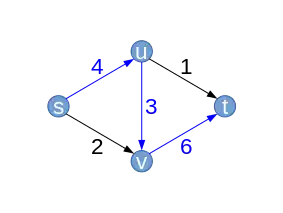 | ||||||||||||||||||
| Flot | 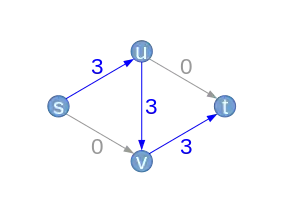 |
| ||||||||||||||||||
| Graphe résiduel résultant (avec les nouvelles capacités résiduelles ) | 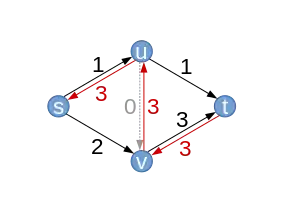 |
| ||||||||||||||||||
| Supposons que l'algorithme sélectionne le chemin améliorant . L'augmentation maximale du débit est limitée par la capacité résiduelle . Pour la première fois, on passe par un arête arrière (). Alors que le flot f augmente de 1 le long des arêtes (s,v) et (u,t), il diminue de 1 le long de (u,v).
On peut remarquer que les capacités résiduelles des arêtes arrières sont toujours égales aux poids dans le flot. |
Chemin améliorant (avec capacités résiduelles ) | 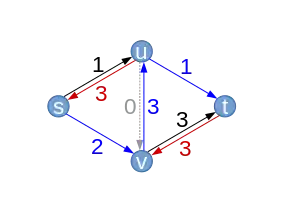 | ||||||||||||||||||
| Flot | 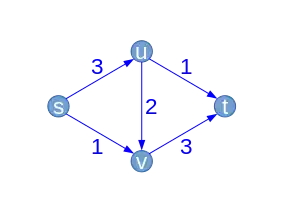 |
| ||||||||||||||||||
| Graphe résiduel résultant (avec les nouvelles capacités résiduelles ) | 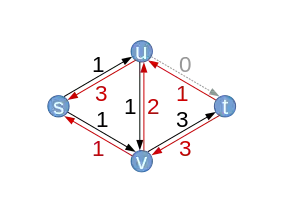 |
| ||||||||||||||||||
| Supposons que l'algorithme choisisse à nouveau le chemin . Cette fois, le débit le long du chemin ne peut être augmenté que de 1. Cela correspond justement au montant par lequel on a diminué (u,v) à l'étape précédente. En effet, l'algorithme peut faire beaucoup de va-et-vient. | Chemin améliorant (avec capacités résiduelles ) | 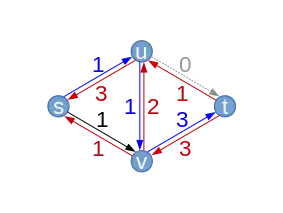 | ||||||||||||||||||
| Flot | 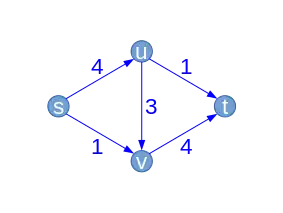 |
| ||||||||||||||||||
| Graphe résiduel résultant (avec les nouvelles capacités résiduelles ) | 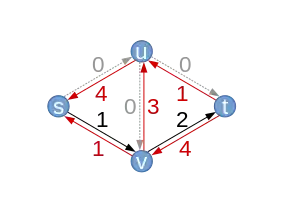 |
| ||||||||||||||||||
| Ici, seul le chemin est possible. Cela augmente alors le débit de 1. Le flot a alors une valeur de . Les arêtes sortantes de la source sont pleinement utilisées donc ce flot est un flot maximal. La coupure au niveau de (s,u) et (s,v) est donc une coupe minimale. On respecte donc bien le Théorème flot-max/coupe-min qui affirme qu'un flot maximal a la même valeur qu'une coupe minimale.
L'algorithme se termine alors car aucun chemin de s à t n'existe dans le graphe résiduel obtenu. On a donc bien obtenu un flot maximal. |
Chemin améliorant (avec capacités résiduelles ) | 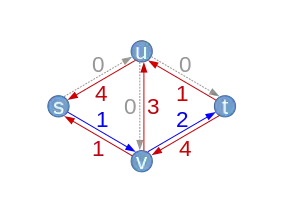 | ||||||||||||||||||
| Flot maximal | 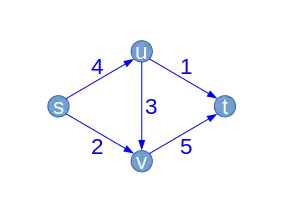 |
| ||||||||||||||||||
| Graphe résiduel résultant (avec les nouvelles capacités résiduelles ) | 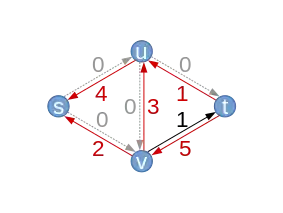 |
|
Propriétés de l'algorithme
Complexité
Le flot maximal est atteint quand plus aucun chemin améliorant ne peut être trouvé. Cependant, il n'y a aucune certitude que cette situation soit atteinte, mais la réponse sera correcte si l'algorithme se termine. Dans le cas où l'algorithme s'exécute indéfiniment, le flot peut même ne pas converger vers le flot maximum. Néanmoins, cette situation ne se produit qu'avec des valeurs de flot irrationnelles. Lorsque les capacités sont des entiers, le temps d'exécution de l'algorithme de Ford-Fulkerson est borné par (voir les notations de Landau), où est le nombre d'arêtes dans le réseau de flot et est la valeur du flot maximal. En effet, chaque chemin augmentant peut être trouvé en et augmente le débit d'une quantité entière d'au moins avec comme borne supérieure.
Une variante de l'algorithme de Ford-Fulkerson avec terminaison garantie et un temps d'exécution indépendant de la valeur de flot maximal est l' algorithme d'Edmonds-Karp, qui a une complexité temporelle en .
Terminaison
Si les capacités des arêtes sont des entiers, l'algorithme se termine.
On peut le démontrer par l'absurde, en supposant que l'algorithme ne se termine pas. En considérant la suite des flots calculés, on distingue plusieurs propriétés :
- la suite est strictement croissante ;
- elle est majorée par la valeur du flot maximal ;
- elle est à valeurs entières.
Cette suite entière est infinie, majorée et strictement croissante, ce qui est absurde.
Exemple pour lequel l'algorithme ne termine pas
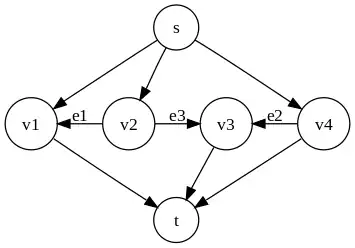
On s'intéresse au graphe suivant, qui a pour sommet source , pour sommet puits . Les arêtes , et ont pour capacités respectives , et . La capacité des autres arêtes est fixée à . On a choisi la constante de sorte que . On considère l'exécution de l'algorithme choisissant les chemins suivants, où on note , et .
| Étape | Chemin choisi | Augmentation du flot | Capacité residuelle | ||
|---|---|---|---|---|---|
| 0 | |||||
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
On remarque qu'après les étapes 1 et 5, les capacités résiduelles des arêtes , et sont respectivement de la forme , et et le flot ajouté est où . Ainsi, par récurrence on pourra toujours répéter la boucle de chemins , , et tout en ajoutant un flot strictement positif car les capacités résiduelles resteront toujours de la forme , et à la fin de l'exécution sur les chemins. L'algorithme ne termine donc pas sur cette entrée. Le fait que l'on ait une capacité non entière est cruciale car elle permet d'avoir une suite de taille de flot infinie strictement croissante et majorée[2].
Notes et références
- (en) L. R. Ford et D. R. Fulkerson, « Maximal Flow Through a Network », Canadian Journal of Mathematics, vol. 8, 1956/ed, p. 399–404 (ISSN 0008-414X et 1496-4279, DOI 10.4153/CJM-1956-045-5, lire en ligne, consulté le )
- Uri Zwick, « The smallest networks on which the Ford–Fulkerson maximum flow procedure may fail to terminate », Theoretical Computer Science, vol. 148, no 1, , p. 165–170 (DOI 10.1016/0304-3975(95)00022-O
 )
)
Voir aussi
Article connexe
- L'algorithme d'Edmonds-Karp est une spécialisation de l'algorithme de Ford-Fulkerson de résolution du problème de flot maximum dans un réseau.
Liens externes
- Applets Java de démonstration
- Un article de vulgarisation : Xavier Caruso et Lionel Fourquaux, « Au feu les pompiers », sur Images des Maths (consulté le )
Bibliographie
- A simple algorithm for finding maximal network flows and an application to the Hitchock problem (FORD L.R., FULKERSON D.R), Rand Report Rand Corporation, Santa Monica, .
- Lester R. Ford et Delbert R. Fulkerson, « Maximal flow through a network », Canadian journal of Mathematics, vol. 8, no 3, , p. 399-404
- The transhipment problem (ORDEN A.), Management Science 2, 1956.
- Sur la déficience d'un réseau infini (BERGE C.), Comptes rendus de l'Académie des Sciences 245, 1957.
- Invitation à la recherche opérationnelle (KAUFMANN A., FAURE R.) Dunod Entreprise, 1979.
- Contribution de la théorie des graphes à l'étude des problèmes d'ordonnancement (ROY B.) Congrès international de recherche opérationnelle, 1960.
- Lester Randolph Ford et Delbert Ray Fulkerson, Flows in Networks, Princeton, NJ, Princeton University Press,
- Ravindra K. Ajuha, Thomas L. Magnanti et James B. Orlin, Network flows - theory, algorithms and applications, Prentice Hall,
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest et Clifford Stein, Introduction to algorithms, MIT Press,
- Jon Kleinberg et Eva Tardos, Algorithms design, Pearson Education India,
























































































