Écoulement en charge

${\displaystyle Z+{P_{1} \over \rho g}+{v^{2} \over 2g}=H=C^{ste}}$

avec

• ${\displaystyle Z}$ = altitude (en m)
• ${\displaystyle P_{1}}$ = pression au point 1 (en Pa ou N/m²)
• ${\displaystyle \rho }$ = masse volumique en un point (en kg/m³)
• ${\displaystyle g}$ = accélération de la pesanteur (en N/kg ou m/s²)
• ${\displaystyle v}$ = vitesse du fluide au point 1 (en m/s)
• ${\displaystyle H}$ = charge totale

${\displaystyle Z_{1}+{P_{1} \over \rho g}+{v_{1}^{2} \over 2g}=Z_{2}+{P_{2} \over \rho g}+{v_{2}^{2} \over 2g}+h_{w12}}$

avec

• ${\displaystyle Z}$ = altitude (en m)
• ${\displaystyle P}$ = pression en un point (en Pa ou N/m²)
• ${\displaystyle \rho }$ = masse volumique en un point (en kg/m³)
• ${\displaystyle g}$ = accélération de la pesanteur (en N/kg ou m/s²)
• ${\displaystyle v}$ = vitesse du fluide en un point (en m/s)
• ${\displaystyle h_{w12}}$ = pertes de charge entre les points 1 et 2

Le calcul des pertes de charges dans un réseau sous pression est un élément essentiel de l’hydraulique sous pression. Comme pour les autres domaines de l’hydraulique, il existe différentes formules empiriques permettant d’estimer ces pertes d’énergies.

La loi de Hagen-Poiseuille donne, dans le cas d’un écoulement laminaire dans une conduite circulaire, la relation entre diamètre et débit[4] - [5].

L’équation de Hazen-Williams permet de calculer les pertes de charge dues à la rugosité des conduites. À la différence de la formule de Poiseuille, limitée aux écoulements à très faible vitesse dans des conduites de petit diamètre, elle permet de décrire les écoulements turbulents de l'eau[3].

${\displaystyle Q=0,849\;C\,A\,R_{h}^{0,63}\,J^{0,54}}$

avec

• ${\displaystyle Q}$ = débit volumique dans la conduite (en m³/s)
• ${\displaystyle C}$ = coefficient de rugosité de Hazen-Williams du matériau constituant la conduite (nombre sans dimension)

La loi de Darcy - Weisbach permet le calcul des pertes de charges linaires dues aux frottements dans le cas de l’eau[6].

${\displaystyle h_{r}=\lambda {L \over D}{V^{2} \over 2g}}$

avec

• ${\displaystyle L}$ = longueur de la conduite considérée (en m)
• ${\displaystyle D}$ = diamètre de la conduite (en m)
• ${\displaystyle V}$ = vitesse du fluide (en m/s)
• ${\displaystyle g}$ = accélération de la pesanteur (en N/kg ou m/s²)
• ${\displaystyle \lambda }$ = coefficient de frottement (sans unité)

Plusieurs formules permettent de calculer le coefficient lambda suivant le régime d'écoulement.

Dans le cas d'un régime laminaire :

${\displaystyle \lambda ={64 \over R_{e}}}$

Dans le cas d'un régime turbulent :

La formule de Colebrook - White permet de calculer le coefficient lambda de pertes de charges linaires dues aux frottements et à la viscosité[7].

${\displaystyle {\frac {1}{\sqrt {\lambda }}}=-2log({\frac {2,51}{Re{\sqrt {\lambda }}}}+{\frac {k}{3,7D}})}$

avec :

• ${\displaystyle \lambda }$ = coefficient de perte de charge linéaire
• ${\displaystyle Re}$ = nombre de Reynolds
• ${\displaystyle D}$ = diamètre de la conduite (m)
• ${\displaystyle k}$ = la rugosité de la canalisation

Suivant cette formule, on voit que le coefficient lambda dépend à la fois de la rugosité de la conduite et de la viscosité du fluide.

La formule empirique de Blasius permet de calculer le coefficient lambda pour une valeur du nombre de Reynolds inférieure à 10⁵ [8] - [9].

${\displaystyle \lambda ={\frac {0,3164}{R_{e}^{0,25}}}}$

avec :

• ${\displaystyle \lambda }$ = coefficient de perte de charge linéaire
• ${\displaystyle Re}$ = nombre de Reynolds

Les formules de Lechapt et Calmon sont une simplification de la formule de Colebrook – White et permettent à l’aide de coefficients fonctions de la rugosité de calculer les pertes de charges linéaires avec une précision relativement bonne (maximum 3 % d'écart relatif) dans leur domaine d’application (fluide = eau, vitesses comprises entre 0,4 m/s et 2,0 m/s, température de l’eau de 10 °C)[10] - [11].

${\displaystyle J=L\times {Q^{M} \over D^{N}}}$

avec

${\displaystyle Q}$ = débit en m³/s

${\displaystyle D}$ = diamètre en m

${\displaystyle J}$ = pertes de charges en mm/m

Diagramme de Moody.

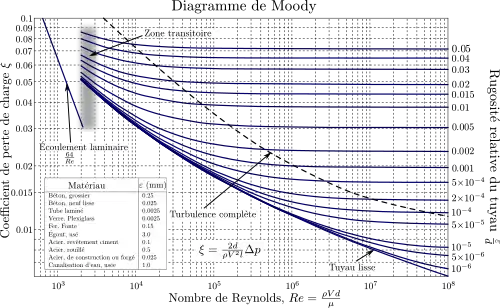
Établi grâce aux travaux de Nikuradse, le diagramme de Moody, du nom de l'ingénieur américain Lewis Ferry Moody, permet de déterminer le coefficient lambda des pertes de charge en fonction du nombre de Reynolds pour différents types d’écoulements et de rugosités[3].

La formule de Chézy est dérivée de celle de Darcy – Weisbach[2] - [12].

${\displaystyle h_{w}=1,1\beta {Q^{2} \over K^{2}}L}$

avec

• ${\displaystyle \beta }$ = coefficient de vitesse (donné par des tables)
• ${\displaystyle Q}$ = débit en m³/s
• ${\displaystyle K}$ = module de débit
• ${\displaystyle L}$ = longueur de la conduite considérée (en m)

Pour le calcul des pertes de charges ponctuelles, il existe pour chaque cas particulier une ou plusieurs formules permettant d’approximer les pertes d’énergies locales. Ces formules sont de la forme suivante[2] :

${\displaystyle h_{s}=\zeta _{s}{V^{2} \over 2g}}$

avec

• ${\displaystyle \zeta _{s}}$ = coefficient propre à chaque type de perte de charge singulière
• ${\displaystyle V}$ = vitesse du fluide (en m/s)
• ${\displaystyle g}$ = accélération de la pesanteur (en N/kg ou m/s²)

Il existe aujourd’hui de nombreux modèles de simulation plus ou moins détaillés permettant le calcul et le dimensionnement des conduites et de systèmes complexes tout entier incluant les réseaux, les réservoirs et les différents organes de contrôle tels que les pompes, les vannes etc. De même qu’il est aujourd’hui possible de calculer précisément les pertes de charges singulières grâce à des modèles numériques.