Zome
Un zome est une forme géométrique composée de losanges agencés en double spirale, dont la trame se veut harmonieuse. Les zomes sont également des constructions de type polyédrique, réalisées en général en matériaux légers. La structure du zome est présente dans différents domaines :
- Animal (alvéoles d'abeilles) ;
- Végétal (ananas, pomme de pin, tournesol…) ;
- Architecture (dĂ´mes,...) ;
- Jeux de construction.
Généralités
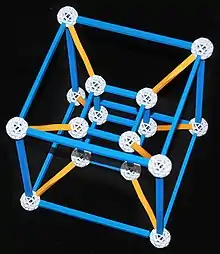
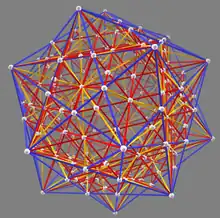
Concept créé aux États-Unis dans les années 1960, le mot « zome » (contraction de « zonohedron » et « dome ») a été inventé en 1968 par Steve Durkee[1]. Le zome est, habituellement, une habitation individuelle en bois et en forme de dôme partant d’un polygone régulier comme base. Le dôme est constitué de formes géométriques, les zonoèdres. Ces constructions peuvent se fondre dans le paysage et créer un cadre de vie novateur. Le concept a été développé par l'Américain Steve Baer (en) pour la construction de dômes, puis ce dernier en a décliné le jeu Zometool avec Marc Pelletier and Paul Hildebrandt à partir des années 1970[1].
En France, l'architecte Jean Soum est considéré comme l'un des pionniers de l'autoconstruction de zomes et de l'éco-habitat bio-dynamique[2]. En 1975, celui-ci se penche sur le concept en rentrant d'un voyage d'étude au Nouveau-Mexique. En 1977, il construit son premier zome dans les Pyrénées ariégeoises. Depuis, plus de 200 zomes ont été bâtis dans l'Hexagone dont une centaine selon ses conseils. En , afin de lui rendre hommage, le festival Festizome était organisé dans la station pyrénéenne de Guzet (Couserans)[2]. Jean Soum étudiait alors le projet de construction en Champagne d'un zome de 22 mètres de diamètre et dix mètres de haut et disposant d'environ 250 facettes ; ce qui en ferait le plus grand zome du Monde.
Géométrie des zomes
La géométrie des zomes est un monde varié où le cube est une des plus simples formes. Pour comprendre la géométrie des zomes il est nécessaire d'appréhender quelques notions :
- Zonogone[3] : polygone possédant un nombre pair de côtés parallèles 2 à 2 ;
- Polyèdre : volume limité par des polygones ;
- Zonoèdre : polyèdre dont toutes les faces sont des zonogones.
Rhombizonoèdres polaires de révolution
Ce sont des zonoèdres avec des faces en forme de losanges (rhombe) possédant une symétrie de révolution autour d'un axe avec deux sommets sur l'axe (pôles).
Ils sont repérés par :
- Un nombre d'ordre (ordre de symétrie) qui va gouverner le nombre total de faces et leur organisation en couronnes ;
- Un nombre de forme qui conduit à un volume plus ou moins étiré ou aplati ;
- Une taille (le mĂŞme Ă une Ă©chelle plus ou moins grande).
Nombre d'ordre
Il détermine le nombre de facettes, le nombre de niveaux, la forme et le nombre de côtés du polygone de la base.
Nombre de forme
Ce nombre gouverne la forme, c’est-à -dire les proportions entre largeur et hauteur, mais aussi la forme particulière des facettes losanges. La forme du losange résulte de la proportion de ses deux diagonales. Des valeurs particulières du nombre de forme donneront des esthétiques différentes.
Fonctionnalité
Les zomes conviennent pour former des habitations, un zome unique avec ou sans extension ou bien un ensemble de zomes peuvent constituer un habitat. Ils peuvent aussi servir d'abri, de cabane, de serre, d'espaces d'activités collectives, les possibilités sont grandes. Selon sa destination, les formes, les arrangements, les techniques peuvent être différentes.
Type
Dans la plupart des constructions, le zome issu d'un rhombizonoèdre est érigé avec axe vertical. Les zomes à axe vertical sont esthétiques et équilibrés.
Une coupe à travers une zone équatoriale donnera des facettes verticales issues du sol (des murs verticaux surmontés d'une coupole), du moins pour les zomes à nombre pair. Cette forme est choisie pour mieux intégrer les ouvertures et pour une meilleure habitabilité. On peut aussi positionner le zome avec axe incliné ou horizontal.
Galerie
Zome nomade en tube et toile.
Zome artistique décoratif en verre.
Zome 13 courbe.
Zome 12 bois et toile de 8,5m de haut
Notes et références
- (en) About us - Zometool.com
- Jean Soum, l'Ariégeois ami des zomes - La Dépêche, 23 juin 2015
- « Zonogone », sur mathcurve.com (consulté le )
Annexes
Bibliographie
- Jean Soum, Le zome : vivre sous une belle étoile, Toulouse/La Sauzière, J. Soum / diff. les Amis des zomes, , 96 p. (ISBN 978-2-9536582-0-0)
Liens externes
- Z5omes Application gratuite d'aide Ă la conception de Zomes
- Modéliser un Zome - Plugin Sketchup Open-Source de modélisation de Zome
- Zome Creator - Source du Logiciel libre de modélisation de Zome
- (en) Eric W. Weisstein, « Zome », sur MathWorld
- Zome Dome et Cie - Ardheia.fr (programme de calcul et de visualisation des zomes)
- (fr+en) Heliss.com
- Arti-zome.fr (construction de zomes en France)
- Construire un Zome - Archilibre.org
- (en) Is there a basic geometric unit? - Dome-scape.com
- Construction d'un zome en montagne - Association de bulles en bulles