Treillis modulaire

Dans un treillis non modulaire, il peut exister des éléments ${\displaystyle b}$ qui vérifient la loi de modularité pour des éléments quelconques ${\displaystyle a}$ et ${\displaystyle x}$, pourvu que ${\displaystyle x\leq b}$. Un tel élément ${\displaystyle b}$ est appelé un élément modulaire. Plus généralement, on peut considérer des couples ${\displaystyle (a,b)}$ d'éléments qui vérifient la loi de modularité pour tous les éléments ${\displaystyle x}$. Un tel couple est appelée un couple modulaire, et il existe plusieurs généralisations de la notion de modularité liées à la notion de semi-modularité qui s'appuient sur ce concept.

La loi de modularité peut être vue comme une loi associative restreinte entre les deux opérations d'un treillis, analogue à la loi associative ${\displaystyle \lambda (\mu x)=(\lambda \mu )x}$, pour les espaces vectoriels, entre la multiplication dans le corps de base et la multiplication scalaire dans l'espace. La restriction ${\displaystyle x\leq b}$ est nécessaire car elle résulte de l'équation

${\displaystyle x\vee (a\wedge b)=(x\vee a)\wedge b}$.

On vérifie facilement que ${\displaystyle x\leq b}$ implique ${\displaystyle x\vee (a\wedge b)\leq (x\vee a)\wedge b}$ dans tout treillis. Par conséquent, la loi de modularité peut également être formulée comme suit :

Loi de modularité (variante)

${\displaystyle x\leq b}$ implique ${\displaystyle x\vee (a\wedge b)\geq (x\vee a)\wedge b}$ .

Si on remplace ${\displaystyle x}$ par ${\displaystyle x\wedge b}$, la loi de modularité peut être formulée comme suit par une équation sans implication :

Loi de modularité (autre variante)

${\displaystyle (x\wedge b)\vee (a\wedge b)=\left[(x\wedge b)\vee a\right]\wedge b}$ .

Cela montre (en utilisation la terminologie d'algèbre universelle) que les treillis modulaires forment une sous-variété de la variété des treillis. Par conséquent, toutes les images homomorphes, tous les sous-treillis et produits directs de treillis modulaires sont à nouveau modulaires.

Diagramme de Hasse de ${\displaystyle N_{5}}$, le plus petit treillis non modulaire.

Tout treillis distributif est modulaire[1] - [2].

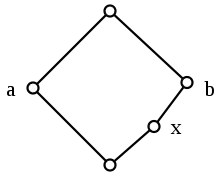
Le plus petit treillis non modulaire est le « treillis pentagonal » ${\displaystyle N_{5}}$ composé de cinq éléments ${\displaystyle 0,1,x,a,b}$ avec ${\displaystyle 0<x<b<1,0<a<1}$, et avec ${\displaystyle a}$ incomparable à ${\displaystyle x}$ ou à ${\displaystyle b}$. Pour ce treillis, on a

${\displaystyle x\vee (a\wedge b)=x\vee 0=x<b=1\wedge b=(x\vee a)\wedge b}$,

en contradiction avec la loi de modularité. Tout treillis non modulaire contient une copie de ${\displaystyle N_{5}}$ en tant que sous-treillis.

Le treillis des sous-modules d'un module sur un anneau est modulaire. En particulier, le treillis des sous-groupes d'un groupe abélien est modulaire.

Le treillis des sous-groupes normaux d'un groupe est modulaire. Mais en général, le treillis des sous-groupes d'un groupe n'est pas modulaire. Par exemple, le treillis des sous-groupes du groupe diédral d'ordre 8 n'est pas modulaire[1].

• 
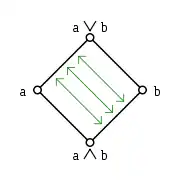  Dans un treillis modulaire, les fonctions ${\displaystyle \phi }$ et ${\displaystyle \psi }$ indiquées par les flèches sont des isomorphismes inverses l'un de l’autre.
• 
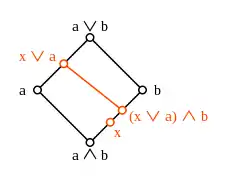  Contre-exemple au théorème d'isomorphisme en diamant dans un treillis non modulaire

Pour deux éléments quelconques ${\displaystyle a,b}$ d'un treillis modulaire, on considère les intervalles ${\displaystyle \left[a\wedge b,b\right]}$ et ${\displaystyle \left[a,a\vee b\right]}$. Les applications

${\displaystyle \phi \colon \left[a\wedge b,b\right]\to \left[a,a\vee b\right]}$ et

${\displaystyle \psi \colon \left[a,a\vee b\right]\to \left[a\wedge b,b\right]}$

définies par ${\displaystyle \phi (x)=x\vee a}$ et ${\displaystyle \psi (x)=x\wedge b}$ préservent l'ordre entre ces intervalles. La fonction composée ${\displaystyle \psi \phi }$ est une application préservant l'ordre de l'intervalle ${\displaystyle \left[a\wedge b,b\right]}$ dans lui-même qui vérifie aussi l'inégalité ${\displaystyle \psi (\phi (x))=(x\vee a)\wedge b\geq x}$ . L'exemple donné ci-dessus montre que cette inégalité n'est en général pas une égalité. Dans un treillis modulaire en revanche, l'égalité est toujours satisfaite. Étant donné que le treillis dual d'un treillis modulaire est à nouveau modulaire, la fonction ${\displaystyle \phi \psi }$ est de même la fonction identité sur ${\displaystyle \left[a,a\vee b\right]}$ ; de sorte que ${\displaystyle \phi }$ et ${\displaystyle \psi }$ sont des isomorphismes entre ces deux intervalles.

Ce théorème est connu sous le nom de théorème d'isomorphisme des treillis modulaires, ou parfois de théorème d'isomorphisme en diamant (pour les treillis modulaires). Un treillis est modulaire si et seulement si le théorème d'isomorphisme du diamant est satisfait par chaque paire d'éléments.

Le théorème d'isomorphisme pour les treillis modulaires est analogue au troisième théorème d'isomorphisme en algèbre, et il est une généralisation du théorème de correspondance.

Le treillis hexagonal centré ${\displaystyle S_{7}}$, aussi noté ${\displaystyle D_{2}}$, est M-symétrique mais n'est pas modulaire.

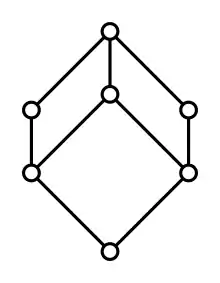
Dans un treillis, un couple modulaire est une couple ${\displaystyle (a,b)}$ d'éléments qui vérifie l'égalité

${\displaystyle (x\vee a)\wedge b=x}$ pour tout ${\displaystyle x}$ tel que ${\displaystyle a\wedge b\leq x\leq b}$ .

En d'autres termes, un couple modulaire est un couple pour lequel la moitié du théorème d'isomorphisme du diamant est vraie. Une paire modulaire est une paire d'éléments telle les deux couples ${\displaystyle (a,b)}$ aussi bien que ${\displaystyle (b,a)}$ sont des couples modulaires. Un élément ${\displaystyle b}$ est un élément modulaire (à droite) si le couple ${\displaystyle (a,b)}$ est modulaire pour tout ${\displaystyle a}$ .

Un treillis dans lequel, pour chaque couple modulaire ${\displaystyle (a,b)}$, le couple ${\displaystyle (b,a)}$ est également modulaire est appelé un treillis M-symétrique[3]. Puisqu'un treillis est modulaire si et seulement si chaque paire d'éléments est modulaire, tout treillis modulaire est M-symétrique. Dans le treillis ${\displaystyle N_{5}}$, le couple ${\displaystyle (b,a)}$ est modulaire, mais pas le couple ${\displaystyle (a,b)}$. Le treillis ${\displaystyle N_{5}}$ n'est donc pas M-symétrique. Le treillis hexagonal centré ${\displaystyle S_{7}}$ est M-symétrique, mais n'est pas modulaire. Comme ${\displaystyle N_{5}}$ un sous-ensemble de ${\displaystyle S_{7}}$, il en résulte que les treillis M-symétriques ne forment pas une sous-variété de la variété des treillis.

La notion de M-symétrie n'est pas auto-duale. Une paire modulaire duale est une paire qui est modulaire dans le treillis dual, et un treillis est appelé M-symétrique dual ou M^*-symétrique si le treillis dual est M-symétrique. On peut montrer qu'un treillis fini est modulaire si et seulement s'il est M-symétrique et M^*-symétrique. La même équivalence vaut pour les treillis infinis qui satisfont la condition de chaîne ascendante (ou la condition de chaîne descendante).

D'autres notions moins courantes sont étroitement liés aux concepts précédents. Un treillis est à symétrie croisée si, pour chaque couple modulaire ${\displaystyle (a,b)}$, le couple ${\displaystyle (b,a)}$ est dual modulaire. La symétrie croisée implique la M-symétrie, mais pas la M^*-symétrie. Par conséquent, la symétrie croisée n'est pas équivalente à la symétrie croisée duale.

Un treillis avec un plus petit élément 0 est appelé ⊥-symétrique si, pour chaque couple modulaire ${\displaystyle (a,b)}$, telle que ${\displaystyle a\wedge b=0}$, le couple ${\displaystyle (b,a)}$ est également modulaire.

Treillis modulaire libre engendré par trois éléments {x,y,z}

La définition de la modularité est due à Richard Dedekind. Dans un article de 1897, « Über Zerlegungen von Zahlen durch ihre größten gemeinsamen Teiler », et en 1900, « Über die von drei Moduln erzeugte Dualgruppe », il introduit les treillis qu'il a appelés groupes doubles (allemand : Dualgruppen) et il a observé que les idéaux satisfont ce que nous appelons aujourd'hui la loi modulaire. Il a également observé que pour les treillis en général, la loi modulaire est équivalente à son dual. Il décrit le treillis modulaire libre à trois générateurs,qui est un treillis à 28 éléments[4].

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Modular lattice » (voir la liste des auteurs).

• [1900] Richard Dedekind, « Ueber die von drei Moduln erzeugte Dualgruppe », Mathematische Annalen, vol. 53, n^o 3,‎ 1^er septembre 1900, p. 371–403 (DOI 10.1007/BF01448979)
• [1949] Garret Birkhoff, « Théorie et applications des treillis », Annales de l'institut Henri Poincaré, vol. 11, n^o 5,‎ 1949, p. 227-240 (lire en ligne, consulté le 3 novembre 2021).
• [1965] Shûichirô Maeda, « On the symmetry of the modular relation in atomic lattices », Journal of Science of the Hiroshima University, vol. 29,‎ 1965, p. 165–170 (lire en ligne)
• [1973] Garrett Birkhoff, Lattice Theory, American Mathematical Society, 1973, 3^e éd. (ISBN 0-8218-1025-1)
• [1967] Hans Hermes, Einführung in die Verbandstheorie, Springer, coll. « Grundlehren der mathematischen Wissenschaften » (n^o 73), , 2^e éd. (DOI 10.1007/978-3-642-86524-4)
• [1971] Gábor Szász, Théorie des treillis, Budapest, Akademiai Kiado, , ix+ 227 zbl=0208.28901
• [1997] Gian-Carlo Rota, « The many lives of lattice theory », Notices of the American Mathematical Society, vol. 44, n^o 11,‎ 1997, p. 1440–1445 (ISSN 0002-9920, lire en ligne)
• [1998] George Grätzer, General Lattice Theory, Birkhäuser, , 2^e éd. (ISBN 3-7643-5239-6)
• [1999] Manfred Stern, Semimodular lattices, Cambridge University Press, 1999 (ISBN 978-0-521-46105-4, lire en ligne )
• [2002] (en) L. A. Skornyakov, « Modular lattice », dans Michiel Hazewinkel, Encyclopædia of Mathematics, Springer, 2002 (ISBN 978-1556080104, lire en ligne)
• [2002] (en) T. S. Fofanova, « Semi-modular lattice », dans Michiel Hazewinkel, Encyclopædia of Mathematics, Springer, 2002 (ISBN 978-1556080104, lire en ligne)
• [2004] Leo Corry, Modern algebra and the rise of mathematical structures, 2nd, 2004 (ISBN 978-3-7643-7002-2), « Richard Dedekind: Numbers and Ideals », p. 64-136

• Groupe modulaire
• Graphe modulaire (en)
• Treillis de Young-Fibonacci
• Groupe d'Iwasawa (en)

• (en) « Modular lattice », sur PlanetMath
• suite A006981 de l'OEIS Nombre de treillis modulaires à n éléments
• Générateur de treillis modulaire. — Une application gratuite qui peut engendrer et visualiser des treillis modulaires.