Transformation de Cayley
En mathématiques, la transformation de Cayley, nommée d'après Arthur Cayley, possède différentes significations voisines. La définition originale est celle d'une application entre les matrices antisymétriques et les matrices de rotation. En analyse complexe, la transformation de Cayley est une application conforme envoyant le demi-plan complexe supérieur sur le disque unité. Enfin, dans la théorie des espaces de Hilbert, c'est une application entre opérateurs linéaires.
Motivation
La transformation de Möbius est une involution de (ou de la sphère de Riemann, en ajoutant les valeurs et ) ; on peut envisager de la généraliser à un anneau unitaire A, puisque si est inversible, son inverse commute avec , donc avec ; le cas des matrices s'avère avoir une signification géométrique importante.
Transformation matricielle
Si A est une matrice carrée n×n (à coefficients réels ou complexes) telle que I + A soit inversible (où I désigne la matrice identité d'ordre n) — autrement dit : telle que –1 ne soit pas valeur propre de A — alors la matrice
c'est-à-dire[1] Ac = (I – A)(I + A)−1, ou encore Ac = (I + A)−1(I – A), vérifie
- .
La transformation de Cayley, M ↦ Mc, est donc une involution de l'ensemble des matrices M telles que I + M soit inversible, c'est-à-dire que
- .
Si A est une matrice réelle et antisymétrique (c'est-à-dire telle que AT = −A), alors I + A est inversible et Q := Ac est une matrice orthogonale dont −1 n'est pas valeur propre, ce qui exclut les matrices orthogonales de déterminant –1 ainsi que certaines matrices de rotation. Réciproquement, si Q est une matrice orthogonale n'ayant pas −1 pour valeur propre, alors Qc est une matrice antisymétrique dont −1 n'est pas valeur propre.
Plus généralement, si A est une matrice complexe antihermitienne alors I + A est inversible et Q := Ac est une matrice unitaire dont −1 n'est pas valeur propre, et réciproquement.
On rencontre parfois une forme légèrement différente, demandant deux applications distinctes, et n'utilisant pas la notation « c » en exposant :
- .
Exemples
- On a .
- Dans le cas 2×2, on a . La matrice de rotation d'un demi-tour, −I, est exclue, même si elle est obtenue comme limite lorsque tan θ⁄2 tend vers l'infini.
- Dans le cas 3×3, on a,où K = w2 + x2 + y2 + z2, et où w = 1. On reconnaît la matrice de rotation correspondant au quaternion (formule que Cayley avait publiée l'année précédente), si ce n'est qu'elle est normalisée pour que w = 1 au lieu de la condition usuelle w2 + x2 + y2 + z2 = 1. Ainsi, le vecteur (x,y,z) est le vecteur unitaire de l'axe de rotation multiplié par tan θ⁄2. Les rotations d'un demi-tour sont à nouveau exclues ; dans ce cas, il s'agit des matrices Q qui sont symétriques.
Autres matrices
Lorsqu'on passe des matrices réelles aux matrices complexes, la transposition est remplacée par la transconjugaison (·H). Cela revient à remplacer le produit scalaire réel standard par le produit scalaire complexe. En fait, on peut généraliser davantage en prenant d'autres choix de matrice adjointe ; la définition ne demande en effet que l'inversibilité de I + M.
Application conforme
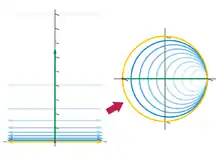
En analyse complexe, la transformation de Cayley est une fonction du plan complexe sur lui-même, donnée par : C'est une fonction homographique, qui peut être prolongée en un automorphisme de la sphère de Riemann (le plan complexe augmenté d'un point à l'infini). On remarquera en particulier que
- W est une application conforme du demi-plan supérieur ouvert de C, sur le disque unité ouvert de C, .
- W est une injection de la droite réelle dans le cercle unité T (les nombres complexes de module 1) ; l'image de R est T privé de 1.
- W est une bijection de la demi-droite des imaginaires i [0, ∞[ sur l'intervalle semi-ouvert [−1, +1[.
- W envoie 0 sur −1, −1 vers i, le point à l'infini vers 1 et −i vers le point à l'infini (W possède un pôle simple en −i)
- W laisse invariant 1⁄2(−1 + √3)(−1 + i) et 1⁄2(1 + √3)(1 − i).
La fonction réciproque de la transformation de Cayley peut s'écrire (en dehors des points à l'infini) sous la forme .
Application entre opérateurs
En dimension infinie, les espaces euclidiens sont remplacés par des espaces de Hilbert, et on ne peut plus parler de matrices. Cependant, il reste possible de généraliser la transformation de Cayley aux opérateurs linéaires :
- , où le domaine de U, dom U, est (A+iI) dom A. L'article endomorphisme autoadjoint donne plus de détails[2].
Voir aussi
Notes
- L'ordre des facteurs n'importe pas. En effet, l'inverse de B := I + A commute avec B donc avec 2I – B = I – A.
- Pour la construction de tels endomorphismes utilisant la transformation de Cayley, se référer à l'article correspondant de la wikipédia anglophone(en).
Références
- Arthur Cayley, « Sur quelques propriétés des déterminants gauches », Journal für die Reine und Angewandte Mathematik (Crelle's Journal),, vol. 32, , p. 119–123 (ISSN 0075-4102, lire en ligne)
- (en) Richard Courant et David Hilbert, Methods of Mathematical Physics, vol. 1, New York, Wiley-Interscience, (ISBN 978-0-471-50447-4)
- (en) Gene H. Golub et Charles F. Van Loan, Matrix Computations, Baltimore, Johns Hopkins University Press, (ISBN 978-0-8018-5414-9)
- (en) N. K. Nikol’skii, Encyclopaedia of Mathematics, Springer-Verlag, (ISBN 978-1-4020-0609-8)



















