Trajectoire orthogonale
En mathématiques, une trajectoire orthogonale est une courbe qui intersecte les courbes d'un faisceau dans le plan orthogonalement.
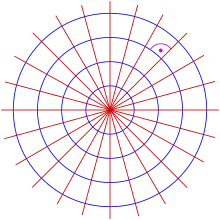
Par exemple, les trajectoires orthogonales d'un faisceau de cercles concentriques sont les droites passant par le centre commun.
Les méthodes usuelles de détermination de trajectoires orthogonales sont données par la résolution d'équations différentielles ; dans les cas simples, on détermine une équation différentielle ordinaire du premier ordre, que l'on résout par séparation des variables pour obtenir l'expression exacte.
Les trajectoires orthogonales sont utilisées en mathématiques dans les systèmes de coordonnées courbes (i.e. coordonnées elliptiques). En physique, le calcul de trajectoires orthogonales permet de déterminer les champs électriques et leurs courbes équipotentielles.
Dans le cas plus général, les courbes intersectant l'ensemble d'un faisceau selon un angle donné fixe sont appelées trajectoires isogonales.
Détermination des trajectoires orthogonales
En coordonnées cartésiennes
On note (Cα) le faisceau de courbes et (Γλ) celui de ses trajectoires orthogonales. On suppose que les courbes de (Cα) vérifient toutes une équation différentielle non paramétrée, qui permettent donc de déterminer la pente de la tangente en un point d'une courbe. Pour trouver les trajectoires orthogonales, il suffit donc de calculer l'opposé de l'inverse de cette pente.
- Forme ordinaire
L'équation différentielle caractérisant (Cα) est de la forme :
Cette valeur f(x , y) correspond à la pente de la tangente de la courbe de (Cα) passant par (x , y), donc la pente de la tangente à la trajectoire orthogonale en ce point vaut -1/f(x , y).
Déterminer les courbes de (Γλ) revient donc à résoudre l'équation différentielle :
- Système différentiel
L'équation différentielle caractérisant (Cα) est de la forme :
Par un raisonnement similaire, on montre que les courbes de (Γλ) vérifient :
- Différentielle
L'équation différentielle caractérisant (Cα) est de la forme :
Par un raisonnement similaire, on montre que les courbes de (Γλ) vérifient :
- Forme implicite non différentielle
Dans le cas où l'équation caractérisant (Cα) est algébrique, de la forme :
on se ramène au cas précédent en différentiant :
Exemples
- Cercles concentriques
L'ensemble des cercles centrés à l'origine vérifie :
qui admet pour différentielle :
Les trajectoires orthogonales vérifient donc
Il s'agit du faisceau de droites passant par l'origine.
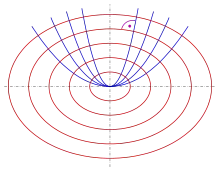
- Paraboles
L'ensemble des paraboles passant par l'origine, d'axe (Oy), vérifie qui admet pour différentielle :
Les trajectoires orthogonales vérifient donc, en utilisant l'équation de base pour supprimer le paramètre α :
Ce sont des ellipses.
En coordonnées polaires
Si l'équation du faisceau est donnée en coordonnées polaires :
la forme différentielle non paramétrée s'écrit
L'équation des trajectoires orthogonales s'écrit alors :
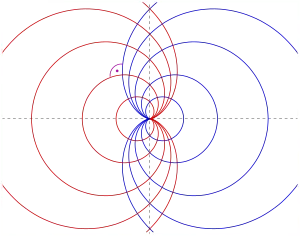
- Exemple
L'équation d'un faisceau de cardioïdes est donné par :
En éliminant α, on obtient l'équation :
L'équation différentielle des trajectoires orthogonales est alors :
Une résolution par séparation des variables donne
soit un faisceau de cardioïdes symétrique à l'original.
Trajectoires isogonales
Quand les courbes recherchées intersectent le faisceau selon un angle θ fixé donné, on parle de trajectoires isogonales.
La relation entre la pente de la tangente à une courbe du faisceau y' et la pente d'une trajectoire isogonale η' en un point (x , y) est donnée par :
Cette égalité se déduit du développement de tan(θ1 + θ2). Pour θ → π/2, on retrouve la relation des trajectoires orthogonales.
Afin de trouver l'équation des trajectoires isogonales, l'équation à résoudre, sous la forme ordinaire, devient :
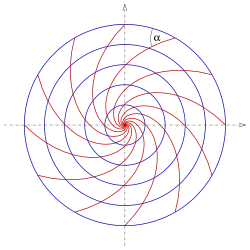
- Exemple
On reprend l'exemple du faisceau de cercles centrés à l'origine, mais on fixe θ = π/4, ce qui donne l'équation suivante à résoudre :
Après un changement de variables z = y/x, l'équation est résoluble par séparation des variables, ce qui donne l'ensemble des courbes solutions d'équation :
soit en coordonnées polaires
Ce sont des spirales logarithmiques.
Méthodes de résolution numérique
Dans le cas où l'équation différentielle des trajectoires n'est pas résoluble exactement, on utilise des méthodes numériques pour les déterminer, usuellement des méthodes de Runge-Kutta.
Applications
- Électromagnétisme
Dans un champ électromagnétique en deux dimensions, les équipotentielles (les courbes de niveaux pour un potentiel donné) sont les trajectoires orthogonales des lignes de champ.
Voir aussi
- Ovale de Cassini
- Coniques confocales
- Trajectoire
- Cercles d'Apollonius
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Orthogonal trajectory » (voir la liste des auteurs).
- (en) A. Jeffrey, Advanced Engineering Mathematics, Hartcourt/Academic Press, , 233 p. (ISBN 0-12-382592-X).
- (en) S. B. Rao, Differential Equations, University Press, , 95 p. (ISBN 81-7371-023-6, lire en ligne).
- (en) R. M. Redheffer et D. Port, Differential Equations: Theory and Applications, Jones & Bartlett, , 63 p. (ISBN 0-86720-200-9, lire en ligne).
- (de) H. Heuser, Gewöhnliche Differentialgleichungen : Einführung in Lehre und Gebrauch, Vieweg+Teubner, , 120 p. (ISBN 978-3-8348-0705-2, lire en ligne).
- (en) Morris Tenenbaum et Harry Pollard, Ordinary Differential Equations, Courier Dover, coll. « Dover Books on Mathematics », (ISBN 9780486134642, lire en ligne), p. 115.
- Jean-Pierre Demailly, Analyse numérique et équations différentielles, Les Ulis, EDP Sciences, , 343 p. (ISBN 2-86883-891-X).
Liens externes
- (en) Exploring orthogonal trajectories - application permettant de tracer des familles de courbes et leurs trajectoires orthogonales
- LIGNES DE CHAMP, LIGNES ORTHOGONALES, SYSTÈME DOUBLE ORTHOGONAL sur Mathcurve


























