Théorie géométrique des groupes
La théorie géométrique des groupes est un domaine des mathématiques pour l'étude des groupes de type fini à travers les connexions entre les propriétés algébriques de ces groupes et les propriétés topologiques et géométriques des espaces sur lesquels ils opèrent. Les groupes sont vus comme des ensembles de symétries ou d'applications continues sur ces espaces.
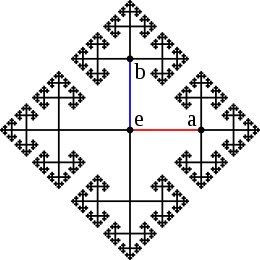
Le graphe de Cayley du groupe libre à deux générateurs, a et b
Une autre idée importante de la théorie géométrique des groupes est de considérer les groupes de type fini eux-mêmes comme des objets géométriques, généralement via le graphe de Cayley du groupe étudié.
Voir aussi
Articles connexes
Liens externes
- (en) Cornelia Druţu et Michael Kapovich (de), « Lectures on Geometric Group Theory »,
- (en) Daniel T. Wise, « What is Geometric Group Theory? », sur Université McGill
- (en) Clara Löh (de), « Geometric group theory, an introduction », sur mathematik.uni-regensburg.de
Bibliographie
(en) Martin Bridson et André Haefliger, Metric Spaces of Non-Positive Curvature, Springer, coll. « Grund. math. Wiss. » (no 319), (lire en ligne)
Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.