Métrique des mots
Dans la théorie des groupes, une branche des mathématiques, une métrique des mots sur un groupe G est une distance sur G, liée au choix préalable d'une partie génératrice S de G : la distance entre deux éléments g, h de G mesure l'efficacité avec laquelle leur « différence » g−1h peut être exprimée comme un mot sur S. La métrique des mots sur G est très étroitement liée au graphe de Cayley de (G, S) : la distance d(g, h) est la longueur du plus court chemin dans le graphe de Cayley entre g et h.
Différents choix de parties génératrices donneront en général des métriques différentes. Bien que cela semble à première vue être une faiblesse dans le concept de la métrique des mots, cela peut être exploité afin de prouver des théorèmes sur les propriétés géométriques des groupes, comme cela se fait dans la théorie géométrique des groupes.
Exemples
Le groupe ℤ des entiers
Le groupe des entiers est engendré par l'ensemble . L'entier peut être exprimé comme un mot de longueur 5 sur ces générateurs. Mais le mot qui exprime plus efficacement est un mot de longueur 3. La distance entre 0 et -3 dans la métrique des mots associée à cette partie génératrice est donc égale à 3. Plus généralement, la distance entre deux nombres entiers et dans cette métrique des mots est égale à , parce que le plus court mot représentant la différence est de longueur égale à .
Le groupe ℤ⊕ℤ
Pour un exemple plus visuel, les éléments du groupe peuvent être vus comme des vecteurs dans le plan cartésien avec des coordonnées entières. Le groupe est engendré par les vecteurs unité usuels , et leurs opposés respectifs , . Le graphe de Cayley de peut être vu dans le plan comme une grille infinie de rues d'une ville, où chaque ligne verticale ou horizontale avec des coordonnées entières est une rue, et chaque point de <. Chaque segment horizontal entre deux sommets représente le vecteur ou , selon que le segment est traversé dans un sens ou dans l'autre, et chaque segment vertical représente ou . Une voiture démarrant en et voyageant dans les rues jusqu'à peut faire le trajet de différentes manières. Mais peu importe le trajet suivi, la voiture doit traverser au moins blocs horizontaux et au moins blocs verticaux, pour une distance totale d'au moins 3 + 2 = 5. Si la voiture change de chemin, le trajet peut être plus long, mais la distance minimale parcourue par la voiture, égale à la distance pour la métrique des mots entre et est donc égale à 5.
Plus généralement, étant donnés deux éléments et de , la distance entre et dans la métrique des mots associée à cette partie génératrice est égale à .
Définition
Soit un groupe, soit une partie génératrice de , et supposons que est stable par inversion. Un mot sur l'ensemble est simplement une suite finie dont les coordonnées sont des éléments de . L'entier est appelée la longueur du mot . En appliquant la multiplication de , les coordonnées d'un mot peuvent être multipliées dans l'ordre. Le résultat de cette multiplication est un élément dans le groupe , qui est appelé à l' évaluation du mot . Un cas particulier, le mot vide a pour longueur zéro, et son évaluation est le neutre de .
Étant donné un élément de , sa norme par rapport à l'ensemble est définie comme étant la plus courte longueur d'un mot sur , dont l'évaluation est égale à . Pour deux éléments de , la distance dans la métrique des mots par rapport à est définie par . De manière équivalente, est la plus courte longueur d'un mot sur tel que .
La métrique des mots par rapport à une partie génératrice de satisfait les axiomes d'une distance.
Variantes
La métrique des mots a une définition équivalente formulée en termes plus géométriques en utilisant le graphe de Cayley de par rapport à une partie génératrice . On assigne à chaque arête du graphe de Cayley une métrique de longueur 1, et alors la distance entre deux éléments de est égale à la plus petite longueur d'un chemin du graphe du sommet au sommet (qui peut être paramétrisée pour en faire une géodésique).
La métrique des mots sur peut également être définie sans supposer que la partie génératrice est stable par inversion. Pour ce faire, on commence par symétriser , en le remplaçant par une plus grande partie génératrice consistant en chaque élément de ainsi que son inverse . Ensuite on définit la métrique des mots par rapport à comme la métrique des mots par rapport à sa symétrisation.
Exemple dans un groupe libre
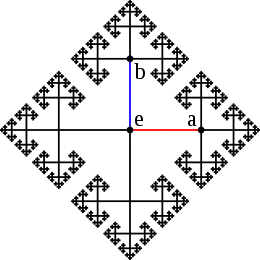
Supposons que est le groupe libre sur l'ensemble à deux éléments . Un mot sur la partie génératrice symétrique est dit réduit si les lettres ne se suivent pas dans , et de même pour les lettres . Chaque élément est représenté par un unique mot réduit, et ce mot réduit est le plus court mot représentant . Par exemple, puisque le mot est réduit et est de longueur 2, la norme est égale à 2, de sorte que la distance entre et est égale à 2 dans la métrique des mots. Cela peut être visualisé en termes de graphe de Cayley, où le chemin le plus court entre et est de longueur 2.
Théorèmes
Isométrie de l'action à gauche
Le groupe agit sur lui-même par multiplication à gauche: l'action de envoie chaque sur . Cette action est une isométrie pour la métrique des mots. En effet, la distance entre et est égale à , qui est la distance entre et .
Invariants bilipschitziens d'un groupe
La métrique des mots sur un groupe n'est pas unique, car différentes parties génératrices symétriques peuvent donner des métriques différentes. Cependant, les métriques de mots sur un groupe de type fini, par rapport à des parties génératrices finies sont Lipschitz-équivalentes : si sont deux parties génératrices symétriques finies de avec les métriques des mots respectives associées , alors il existe une constante tels que, pour tout ,
- .
Cette constante est simplement le maximum de la norme pour la partie génératrice des éléments de et de la norme pour la partie génératrice des éléments de . Cette preuve est également facile : n'importe quel mot sur peut être converti par substitution en un mot sur de même évaluation, augmentant la longueur du mot d'un facteur au plus , et de même pour la conversion de mots sur en mots sur de même évaluation.
L'équivalence lipschitzienne des métriques des mots implique à son tour que le taux de croissance (en) d'un groupe de type fini est un invariant d'isomorphisme du groupe, indépendant du choix d'une partie génératrice finie. Cela implique à son tour que les différentes propriétés de croissance, telles que la croissance polynomiale, le degré de la croissance polynomiale, et la croissance exponentielle, sont des invariants d'isomorphisme.
Invariants de quasi-isométrie d'un groupe
En théorie géométrique des groupes, les groupes sont étudiés à travers leurs actions sur des espaces métriques. Un principe qui généralise l'invariance lipschitzienne des métriques des mots sur est que toute métrique des mots finiment générée sur est quasi-isométrique (en) à tout espace métrique géodésique propre sur lequel agit proprement discontinument et cocompactement. Il s'agit du lemme de Svarc-Milnor (en).
Il s'ensuit que toute propriété invariante par quasi-isométrie satisfaite par la métrique des mots sur ou par un tel espace métrique est un invariant d'isomorphisme de . La théorie géométrique des groupes moderne est en grande partie destinée à l'étude des invariants par quasi-isométrie.
Notes et références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Word metric » (voir la liste des auteurs).
- (en) J. W. Cannon, « Geometric group theory », Handbook of Geometric Topology, North-Holland, Amsterdam, 2002 (ISBN 0-444-82432-4), p. 261-305































































