Théorème de Wedderburn
En mathématiques et plus précisément en algèbre, le théorème de Wedderburn affirme que tout corps qui est fini est nécessairement commutatif. Joseph Wedderburn l'a publié en 1905.

Énoncé du théorème
Théorème de Wedderburn. — Tout corps fini est commutatif.
Remarque sur la terminologie : diverses sources, notamment sous l'influence de l'anglais où le mot field désigne un corps commutatif, posent la commutativité de la multiplication dans la définition d'un corps et en particulier pour les corps finis. Le théorème serait alors une tautologie triviale si on interprétait ainsi l'expression « corps fini » qui y figure. L'énoncé ci-dessus doit être lu avec l'autre interprétation où la commutativité de la multiplication dans la définition de « corps » n'est pas exigée. Dans le cas contraire où elle est exigée, on peut énoncer le théorème ainsi: tout corps gauche (encore appelé anneau à division) fini est commutatif. On renvoie à l'article Corps (mathématiques) pour plus de détails sur la terminologie.
Conséquence et généralisation
- Tout anneau sans diviseur de zéro et fini est un corps (a priori non commutatif), puisque la multiplication par un élément non nul, qui est injective par intégrité, est alors aussi surjective dans le cas fini. Le théorème de Wedderburn affirmant l'inexistence d'un corps non commutatif fini, on en conclut qu'un anneau fini sans diviseur de zéro ne peut lui aussi qu'être un corps commutatif.
Histoire
Leonard Eugene Dickson, professeur à l'université de Chicago, publie en 1901 la première présentation moderne de la théorie des corps commutatifs finis[1] - [2] (théorie initiée par Évariste Galois en 1830). Oswald Veblen travaille à cette époque sur les géométries sur des structures finies dans la même université. Joseph Wedderburn les rejoint en 1904-1905 et travaille en étroite collaboration avec eux.
En 1905, Wedderburn et Dickson publient chacun un article où il est démontré que tout corps fini est commutatif. Dicskon attribue le résultat à Wedderburn. En effet, Wedderburn a communiqué une preuve du résultat à Dickson, et celui-ci, alors qu'il doute de sa véracité, finit par découvrir une preuve différente qu'il communique à son tour à Wedderburn. Ce dernier s'en inspire pour deux autres démonstrations qu'il publie, jointes à la première, dans son article. Ce n'est que plus tard que la première démonstration de Wedderburn apparut comme incomplète[3] - [4] - [5].
De nombreuses autres démonstrations de ce théorème, utilisant des outils mathématiques assez différents, ont été proposées depuis[5] - [4]. La première preuve de Wedderburn a elle-même été corrigée de plusieurs façons[4].
Démonstration
La démonstration proposée ici est due à Ernst Witt[6] - [7] en 1931. Elle peut se découper en quatre temps.
K est un espace vectoriel sur son centre
- K est un corps fini. Soient Z son centre (c'est un sous-corps commutatif de K) et q = | Z | le cardinal de Z (qui vaut au moins 2 car Z contient 0 et 1).
- K est un Z-espace vectoriel de dimension finie d = dimZ(K). Le cardinal de K est alors |K| = qd. Il s'agit, pour prouver que K est commutatif c'est-à-dire K = Z, de démontrer que d = 1.
- Pour tout corps intermédiaire Z ⊂ K' ⊂ K, la dimension d' de K' sur Z divise d, puisqu'on vérifie facilement[5] en prenant des bases que d = d''d', où d'' désigne la dimension de K considéré comme espace vectoriel (à gauche) sur le corps (non commutatif a priori) K'. (On pourrait également utiliser simplement le Théorème de Lagrange stipulant que l'ordre de chaque élément d'un groupe divise l'ordre du groupe)
Soient x un élément de K et Zx l'ensemble des éléments de K commutant avec x. Zx est un sous-corps de K contenant Z. D'après le point précédent, dx = dimZ(Zx) divise d.
Formule des classes pour l'action de K× sur lui-même par conjugaison.
Notons K× le groupe multiplicatif de K, constitué des éléments inversibles de K. K× agit sur lui-même par conjugaison par pour .
- Le cardinal de l'orbite d'un élément de K× est où, rappelons, . La conjugaison est triviale sur Z ; les éléments de Z× ont une classe réduite à un élément.
- Si (xi) est une suite de représentants des k orbites non ponctuelles, la formule des classes s'écrit :
soit, en constatant que est l'ensemble des éléments inversibles et commutant avec par "multiplication" de , ce qui implique que est un sous-corps de contenant Z (et donc ) :
En notant
on vient de voir que F(q) = q – 1.
Φd(X) divise F(X) dans Z[X]
La théorie des polynômes cyclotomiques usuels (qui sont à coefficients entiers) démontre l'égalité suivante, si Φe(X) désigne le polynôme cyclotomique d'indice e :
En particulier Φd(X) divise Xd – 1, et pour tout diviseur strict d' de d, Φd(X) divise aussi (Xd – 1)/(Xd' – 1) puisque
pour un certain polynôme C(X) à coefficients entiers : le produit des Φe(X) pour tous les e qui divisent strictement d mais qui ne divisent pas d' .
Par conséquent, Φd(X) divise F(X) dans ℤ[X]. En effet, pour tout dont l'orbite n'est pas ponctuelle, est un diviseur strict de d donc le raisonnement précédent s'applique à et la conclusion suit, vu la définition de F(X).
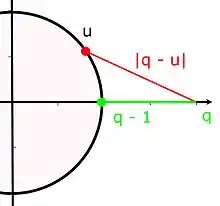
Géométrie des racines primitives d-ièmes
- On a obtenu 0 < q – 1 = F(q) = Φd(q)Q(q), où Q(q) est un entier, nécessairement non nul, donc |Q(q)| vaut au moins 1, si bien que
- Pour tout entier n ≥ 1, , où ui décrit l'ensemble des racines primitives n-ièmes de l'unité. Comme l'illustre la figure ci-contre, si u est une racine primitive n-ième de l'unité avec n > 1, on a |q – u| > q – 1, donc
- Les deux inégalités précédentes entraînent d = 1 ; ainsi K est commutatif. Le théorème est démontré.
Interprétation cohomologique
Le théorème équivaut essentiellement au fait que le groupe de Brauer de tout corps fini K est trivial. Cette reformulation permet la démonstration suivante, plus rapide : comme le quotient de Herbrand (en) est nul par finitude, Br(K) = H2(Kalg/K) coïncide avec H1(Kalg/K), qui est lui-même nul d'après le théorème 90 de Hilbert.
Notes et références
Notes
- (en) Leonard Eugene Dickson, Linear Groups: With an Exposition of the Galois Field Theory (1901), rééd. Dover 2003 (ISBN 9780486495484), Cosimo 2007 (ISBN 9781602062870).
- (en) Rudolf Lidl et Harald Niederreiter, Finite Fields, Cambridge University Press, , 2e éd., 755 p. (ISBN 978-0-521-39231-0, lire en ligne), p. 73.
- (en) K. H. Parshall, « In pursuit of the finite division algebra theorem and beyond: Joseph H M Wedderburn, Leonard E Dickson, and Oswald Veblen », Arch. Internat. Hist. Sci., vol. 33, , p. 274-299.
- (en) M. Adam et B. J. Mutschler, On Wedderburn's theorem about finite division algebra : analyse de l'erreur de la première démonstration de Wedderburn.
- Gabriel Chênevert, Le théorème de Wedderburn : aperçu historique comparatif de diverses preuves, dont celle Theodore Kaczynski, qui n'emploie « que » la théorie des groupes finis.
- (de) Ernst Witt, « Über die Kommutatitivät endlicher Schiefkörper », Abh. Math. Sem. Univ. Hambourg, vol. 8, 1931, p. 413.
- Martin Aigner et Günter M. Ziegler, Raisonnements divins, 2e éd., Springer, 2006, chap. 5 (« Tout corps fini est commutatif »), p. 27-31.
Références
- Pierre Samuel, Théorie algébrique des nombres [détail de l’édition]
- Jean-Pierre Serre, Cours d'arithmétique, [détail des éditions]
- Guy Heuzé, Sur les corps finis, Mathématiques et Sciences Humaines, 1974
- André Warusfel, Structures algébriques finies, Hachette Université, 1971
Articles connexes
- Automorphisme de Frobenius
- Théorème d'Artin-Zorn (en)
- Théorème de Skolem-Noether











![{\displaystyle \exists d_{x_{i}}\in \mathbb {N} [|Z_{x_{i}}^{\times }|=q^{d_{x_{i}}}-1]}](https://img.franco.wiki/i/a62d570f27f7a8f4489c661dd7982bca3c41f280.svg)










