Température négative

En physique statistique le système thermodynamique possède N degrés de liberté et est décrit par les positions q_i et les quantités de mouvement p_i de chacun des éléments constitutifs, liées par les équations canoniques de Hamilton. On définit le volume élémentaire dans l'espace des phases

${\displaystyle \mathrm {d} W=\Pi _{i}\mathrm {d} \mathbf {q} _{i}\mathrm {d} \mathbf {p} _{i}}$

L'équation de Liouville décrit l'évolution temporelle de la densité de probabilité ρ(U,V) d'un état donné dans l'espace des phases. Dans notre cas cette évolution s'effectue sous la contrainte de conservation de l'énergie E du système au cours de toute transformation. Cette contrainte s'écrit

${\displaystyle H(\{\mathbf {q} _{i},\mathbf {p} _{i}\})=E\,,\;\;\;\forall \{\mathbf {q} _{i},\mathbf {p} _{i}\}}$

où H(q_i,p_i) est l'hamiltonien. Elle définit une hypersurface de dimension 2N-1.

Sous l'hypothèse d'ergodicité la densité de probabilité de trouver le système dans l'état {q_i,p_i} est[4] - [5]

${\displaystyle \rho ={\frac {\delta (H-E)}{\omega (E)}}}$

La constante de normalisation ω vaut

${\displaystyle \omega (E)=\int \delta (H-E)\mathrm {d} W}$

L'intégrale de ω s'écrit

${\displaystyle \Omega (E_{i})=\int \Theta (H-E)\mathrm {d} W}$

où Θ est la distribution de Heaviside. Ω représente le nombre d'états d'énergie supérieure ou égale à E_i au contraire de ω qui porte sur tous les états. À partir de là on peut définir de deux manières l'entropie microcanonique[6]

- entropie de Boltzmann		${\displaystyle S(E)=k\ln(\epsilon \omega )}$	où ${\displaystyle \epsilon }$ est une constante arbitraire ayant la dimension d'une énergie,
- entropie de Gibbs		${\displaystyle S_{G}(E)=k\ln(\Omega )}$

On définit les températures d'un système à volume constant par

${\displaystyle T=\left({\frac {\partial E}{\partial S}}\right)_{V}\,,\;\;\;T_{G}=\left({\frac {\partial E}{\partial S_{G}}}\right)_{V}}$

Ces deux températures sont liées par la relation[1]

${\displaystyle T={\frac {T_{G}}{1-{\frac {k}{C_{V}}}}}}$

où C_V est la capacité thermique

${\displaystyle C_{V}=\left({\frac {\partial E}{\partial T_{G}}}\right)_{V}}$

La relation de Gibbs possède au plan théorique des avantages, en particulier respecte la relation de cohérence pour le système microcanonique[1]

${\displaystyle p=T_{G}\left({\frac {\partial S_{B}}{\partial V}}\right)_{E}=-\left\langle {\frac {\partial H}{\partial V}}\right\rangle \neq T\left({\frac {\partial S}{\partial V}}\right)_{E}}$

où ‹.› désigne la moyenne d'ensemble.

La différence entre T et T_G est extrêmement ténue dans les systèmes « habituels » où C_V >> k. Ce n'est pas le cas des systèmes quantiques dont on parle ici.

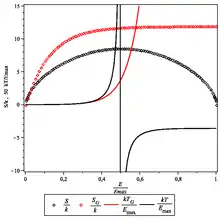
La température T_G d'un tel système est régulière et positive (voir figure).