Surface de subdivision
Dans le domaine de la CAO et des mathématiques, les surfaces de subdivision sont une façon de créer des surfaces lisses développant de plus en plus un maillage linéaire par morceaux. La surface lisse finale, peut être calculée comme la limite du procédé itératif de subdivision de chaque face polygonales en un sous-ensemble de faces approchant mieux la surface lisse finale.
Depuis le début des années 2000, les surfaces de subdivision ont remplacé les NURBS dans les procédés privilégiés de modélisation de personnages et dans la création de la géométrie des décors dans les effets visuels de l'industrie cinématographique.
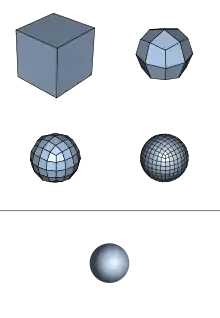
Introduction
Les procédés de subdivision sont par nature des algorithmes récursifs. La méthode débute à partir d'un maillage (ou mesh) donné. Un schéma de subdivision est alors appliqué à ce maillage. Ce procédé agit sur le maillage en le subdivisant, en créant de nouveaux points et de nouvelles faces. La position des nouveaux points est calculée à partir de celle des anciens points les plus proches. Dans certains schémas, les positions des anciens points sont aussi remises à jour à partir des nouveaux points.
Ce procédé produit un nouveau maillage contenant bien plus de faces polygonales que l'ancien maillage. Le nouveau maillage peut alors servir comme données d'entrée au schéma de subdivision, afin de raffiner encore plus.
Cependant le but de l'application itérative d'un schéma de subdivision n'est pas forcément de produire un maillage plus lisse que le maillage d'entrée.
Schéma de subdivision
Les schémas de subdivision surfacique ayant pour but le lissage peuvent être classés en 2 catégories : les schémas interpolants et les schémas approximants.
Les schémas interpolants sont utilisés lorsque les nouveaux points doivent être exactement sur les vecteurs originaux.
Les schémas approximants peuvent ajuster leurs positions. Ce qui donne en général un meilleur lissage, mais l'utilisateur a moins de contrôle sur le résultat final.
Schémas approximants
- Les subdivisions de surface Catmull-Clark (1978)
- Les subdivisions de surface Doo-Sabin, le deuxième schéma de subdivision fut développé par Doo et Sabin (1978) qui appliquèrent avec succès la méthode de Chaikin de la découpe des coins pour courbes et surfaces.
- Les subdivisions de surface Loop
- Les subdivisions de surface Mid-Edge
- Les subdivisions √3
Schémas interpolants
- Papillons, Triangles
- Midedge
- Kobbelt
Références
- Jörg Peters et Ulrich Reif, « The simplest subdivision scheme for smoothing polyhedra », ACM Transactions on Graphics, vol. 16, no 4, , p. 420–431 (ISSN 0730-0301, DOI 10.1145/263834.263851).
- A. Habib and J. Warren: Edge and vertex insertion for a class of C1 subdivision surfaces, Computer Aided Geometric Design 16(4) (May 1999) p.223-247, doi.
- L. Kobbelt: √3-subdivision, 27th annual conference on Computer graphics and interactive techniques, doi.
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Subdivision surface » (voir la liste des auteurs).