Spirale de Cotes
Les spirales de Cotes forment une famille de courbes planes dont beaucoup sont des spirales étudiées par le mathématicien et physicien Roger Cotes quand il s'est intéressé au mouvement à force centrale inversement proportionnelle au cube de la distance.
Éliminant implicitement les cas triviaux du cercle et du mouvement rectiligne, Cotes distingue 5 types de trajectoires[1]:
- les spirales de Poinsot bornées
- les spirales logarithmiques
- les spirales de Poinsot à asymptote
- les spirales hyperboliques
- les épis
- Les cinq cas détaillés par Roger Cotes
 Cas 1 : spirale de Poinsot de type borné.
Cas 1 : spirale de Poinsot de type borné..svg.png.webp) Cas 2 : spirale logarithmique
Cas 2 : spirale logarithmique Cas 3 : spirale de Poinsot de type asymptotique.
Cas 3 : spirale de Poinsot de type asymptotique.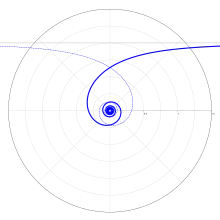 Cas 4 : spirale hyperbolique.
Cas 4 : spirale hyperbolique.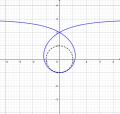 Cas 5 : épi.
Cas 5 : épi.
Il signale que Newton a, quant à lui, déjà évoqué les cas 1 et 5, dans ses Principia[2], livre 1, section VIII, proposition XLI [3] - [4].
Étude cinématique
Puisque le mouvement est à force centrale, il est plan et vérifie la loi des aires.
En coordonnées polaires, cela se traduit par où h est constant.
La force étant inversement proportionnelle au cube du rayon, il existe une constante μ telle que c'est-à-dire
Étude de la trajectoire
Si h est nul, l'angle θ est constant et le mouvement est donc rectiligne.
Dans le cas contraire, est non nul. Le principe[5] consiste alors à déterminer l'expression de u = 1/r en fonction de θ en remplaçant par hu² et en dérivant deux fois par rapport à θ . On obtient une équation différentielle linéaire d'ordre deux, homogène, dont les solutions dépendent du signe de . En posant , on distingue trois cas :
- si , u s'exprime comme combinaison linéaire de fonctions exponentielles. L'orbite est alors une spirale de Poinsot. Sa forme (bornée, logarithme ou avec asymptote) dépend des conditions initiales ;
- si , u est fonction affine de θ , ce qui donne pour une fonction non constante une spirale hyperbolique, et pour une fonction constante un cercle ;
- Si , il existe A et φ tel que et l'orbite est un épi.
Étude de la distance en fonction du temps
La conservation de l'énergie totale (énergie cinétique plus énergie potentielle) permet d'exprimer r2 comme fonction du second degré en t [6]. On peut montrer ainsi que dans le cas où et pour un mouvement non circulaire, le déplacement se fait dans un temps borné inférieurement, ou borné supérieurement ou, dans le cas d'une trajectoire de Poinsot bornée, dans un temps fini.
Notes et références
- Cotes 1722, p. 30.
- Cotes 1722, p. 35.
- Gowing 2002, p. 54.
- Principia 1759, p. 136.
- cf. Exercice 4 de ce Td de physique du lycée Montaigne
- Danby 1992, p. 69.
Bibliographie
- (la) Roger Cotes, Harmonia mensurarum, Robert Smith, (lire en ligne), Pars prima pp 30-35 et Editoris notae pp 117-123.
- Isaac Newton et Émilie du Châtelet, Principes mathématiques de la philosophie naturelle, Desaint et Saillant, (lire en ligne).
- (en) Ronald Gowing, Roger Cotes : Natural philosopher, Cambridge University Press, (présentation en ligne), p. 53-54.
- (en) S. Earnshaw, Dynamics : or an elementary treatise of motion, Cambridge, (lire en ligne), p. 45-49.
- (en) John Danby, Fondamentals of celestials mechanics, , p. 69-70.












