Règle de Cauchy

En mathématiques, la règle de Cauchy, qui doit son nom au mathématicien français Augustin Cauchy, est un critère de convergence pour une série à termes réels ou complexes, ou plus généralement à termes dans un espace vectoriel normé.

Diagramme de décision pour l'application de la règle de Cauchy

Cette règle est parfois confondue avec le « critère de Cauchy » selon lequel, dans un espace complet comme ℝ ou ℂ, toute suite de Cauchy converge.

Énoncé

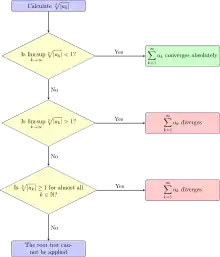
La règle de Cauchy[1] donne un critère de convergence pour une série de terme général $x n$ dans un espace vectoriel normé, en fonction de la limite supérieure[2]

p=\limsup _{n\to +\infty }{\sqrt[{n}]{\left\|x_{n}\right\|}}

La série est :

absolument convergente si $p < 1$ , donc convergente si l'espace est de Banach c'est-à-dire complet ;
grossièrement divergente si $p > 1$ , c'est-à-dire que la suite $(x n)$ ne tend même pas vers 0.

Si $p = 1$ , il y a indécidabilité à défaut d'informations supplémentaires.

La règle s'applique en particulier pour des séries dans ℝ (où la norme est la valeur absolue) ou dans ℂ (où la norme est le module) ou même dans ℝⁿ ou ℂⁿ, complets pour n'importe quelle norme.

Cas p = 1

La série harmonique qui diverge et la série harmonique alternée qui converge vers $ln(2)$ sont deux exemples pour lesquels la limite des $║ x n ║ 1/ n$ — et pas seulement la limite supérieure — vaut 1, car $(1/ n)ln(1/ n)$ tend vers 0.

On montre encore que les réciproques des deux premières propriétés sont fausses :

la série de Dirichlet de terme général $x n = n$ ⁻² est absolument convergente vers $ζ(2)$ alors que pour elle, la limite vaut 1 ;
la série de terme général $x n = (-1) n$ diverge grossièrement alors que pour elle, la limite vaut aussi 1.

Lien avec la règle de d'Alembert

Ce critère de convergence est très proche de celui de d'Alembert, qui spécifie dans sa forme la plus précise que la série de terme général $x n$ :

converge absolument dès que $lim sup (║ x n +1 ║/║ x n ║) < 1$ ;
diverge grossièrement dès que $lim inf (║ x n +1 ║/║ x n ║) > 1$ .

La règle de Cauchy lui est légèrement supérieure de deux points de vue :

stricto sensu, le critère de d'Alembert ne s'applique qu'à une série sans terme nul. On peut toujours sans problème se ramener à ce cas, mais il n'est pas nécessaire de prendre cette précaution avec celui de Cauchy ;
le cas douteux de la règle de d'Alembert est légèrement plus vaste que celui de celle de Cauchy : chaque fois que la règle de d'Alembert conclut quelque chose, celle de Cauchy arrive à la même conclusion, puisqu'il est vrai en général que $\liminf {\tfrac {\|x_{n+1}\|}{\|x_{n}\|}}\leq \limsup {\sqrt[{n}]{\|x_{n}\|}}\leq \limsup {\tfrac {\|x_{n+1}\|}{\|x_{n}\|}}.$ En revanche, il existe des exemples pour lesquels la règle de Cauchy conclut, mais pas celle de d'Alembert[3].

Notes et références

Pour une démonstration, voir par exemple « Règle de Cauchy » dans la leçon sur les séries numériques sur Wikiversité.
Augustin Louis Cauchy, Cours d'analyse de l'École royale polytechnique, 1re partie. Analyse algébrique, 1821 (lire en ligne), p. 132.
Gilles Costantini, « Règles de d'Alembert et de Cauchy pour les séries à termes réels positifs » (version du 2 avril 2015 sur Internet Archive).

Articles connexes

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.