Problème du vendeur de journaux

Le problème dit « problème du vendeur de journaux » est un modèle mathématique simple en recherche opérationnelle (microéconomie) concernant le volume économiquement optimal du stock d’un bien qui sera proposé à une demande aléatoire.

L’analyse de ce problème académique montre que, lorsque des phénomènes stochastiques interviennent dans les données d’un problème d’optimisation, le fait de remplacer ces variables aléatoires par leurs espérances respectives dénature les résultats et conduit à une sous-optimisation. La simplification avantageuse (en termes de résolution) d’une formulation déterministe d’un problème qui ne l’est pas peut induire des prises de décision erronées et coûteuses.

Cadre du problème

Au début de sa journée, un vendeur itinérant achète un certain nombre $\displaystyle q$ de journaux au prix unitaire $\displaystyle c$ afin de les vendre à la criée aux passants des rues, ceci à un prix unitaire $\displaystyle p>c$ (hypothèse).

Ne connaissant pas précisément le volume de ses ventes, le vendeur cherche à déterminer la quantité $\displaystyle q$ lui permettant de maximiser l’espérance de son profit acquis durant sa journée :

s’il choisit $\displaystyle q$ trop grand, il lui restera des journaux invendus qu’il aura acheté au prix $\displaystyle c$ pour les jeter en fin de journée.
s’il choisit $\displaystyle q$ trop petit, il restera des acheteurs potentiels, soit autant de ventes perdues.

Formulations

Stochastique

La fonction objectif (à maximiser) est l’espérance du profit qui, en fonction de la quantité $\displaystyle q$ choisie, s’écrit

\Phi _{S}(q)=p\int _{0}^{q}v\,\rho (v)\,dv+p\,q\int _{q}^{\infty }\rho (v)\,dv\,-c\,q

où $\displaystyle \rho (v)$ la densité de probabilité de la variable aléatoire de la demande.

Les deux premiers termes répertorient les situations où la demande est inférieure (respectivement supérieure) aux disponibilités; le troisième terme concerne les coûts d’acquisition.

Le maximum de $\displaystyle \Phi _{S}(q)$ est atteint pour le choix optimal ${\hat {q}}$ défini par la relation implicite :

F({\hat {q}})=1-c/p

où $\displaystyle F(v)$ est la fonction de répartition cumulative de la demande $\displaystyle v$ définie par $F(v)=\int _{0}^{v}\rho (w)\,dw.$

En effet, pour tout $q\geqslant 0$ , on vérifie :

\Phi _{S}({\hat {q}})-\Phi _{S}(q)=p\int _{q}^{\hat {q}}(v-q)\,\rho (v)\,dv\geqslant 0.

Dans cette dernière relation, en posant $\displaystyle q=0$ (avec $\displaystyle \Phi _{S}(0)=0$ ), on déduit le profit espéré maximal :

\Phi _{S}({\hat {q}})=p\int _{0}^{\hat {q}}v\,\rho (v)\,dv\geqslant 0.

Conséquemment, il existe un choix conduisant à un profit espéré positif.

Déterministe

Bien que la demande soit aléatoire, on suppose qu’elle est déterministe, égale à sa valeur espérée notée ${\bar {v}}$ et de variance nulle. Dans un contexte plus général (et plus complexe), le but d’une telle approximation est de simplifier la résolution. Pour le vendeur de journaux, la fonction objectif (d'une formulation déterministe) s’écrit alors[1] :

\Phi _{D}(q)=p\,\min(q,{\bar {v}})-c\,q

dont la solution est naturellement $q={\bar {v}}$ et le profit maximal est $\Phi _{D}({\bar {v}})=(p-c){\bar {v}}$ .

Puisque $\Phi _{S}({\hat {q}})\geqslant \Phi _{S}({\bar {v}})$ , la solution de cette formulation déterministe érode le profit espéré maximal : elle est sous-optimale.

Exemple numérique

Afin de quantifier la perte de profit espéré causée par la formulation déterministe, admettons les hypothèses suivantes :

la demande $\displaystyle v$ suit une loi log-normale (choisie pour assurer des valeurs positives) d’espérance ${\bar {v}}=$ 100 et d’écart type $\displaystyle \sigma (v)$ considéré comme un paramètre libre pour l’étude,
le prix d’achat : $\displaystyle c=$ 1.0,
le prix de vente : $\displaystyle p=$ 1.1.

Dégradation du profit de la solution obtenue en formulation déterministe

Sous ces conditions, pour toute valeur de $\sigma (v)$ , il est possible de déterminer :

la solution ${\hat {q}}$ ,
le profit espéré associé $\Phi _{S}({\hat {q}})$ ,
le profit espéré $\Phi _{S}({\bar {v}})$ qui prévaudrait avec la solution de la formulation déterministe.

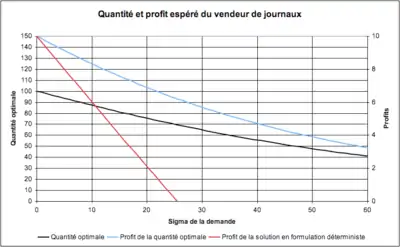
La figure ci-contre visualise ces résultats associés aux deux formulations en fonction de $\displaystyle \sigma (v)$ :

Lorsque la variabilité (sigma) de la demande augmente, la quantité optimale ${\hat {q}}$ décroît (courbe noire, échelle de gauche) afin d’éviter l’achat de journaux qui seront perdus en cas de faible demande.
Le profit espéré de la solution de la formulation stochastique $(\Phi _{S}({\hat {q}}))$ décroît également (courbe bleue, échelle de droite).
Le profit espéré de la solution de la formulation déterministe $(\Phi _{S}({\bar {v}}))$ décroît plus rapidement (courbe rouge, échelle de droite). Il prend même des valeurs négatives à partir d’un sigma relatif $(\sigma (v)/{\bar {v}})$ excédant 25 %.
Même pour un faible sigma relatif de 10 % (valeur 10 sur les abscisses), la formulation déterministe conduit à une érosion significative du profit espéré, soit une perte de l’ordre de 25 %.

Ce simple exemple atteste des dangers encourus par l’application d’une formulation déterministe à un problème qui ne l’est pas. En pratique, il est généralement préférable d’utiliser une distribution $\displaystyle \rho (v)$ mal connue au lieu de l’ignorer.

Intérêt économique des prévisions

Un outil de prévision s’appuyant sur des données statistiques des événements enregistrés par le passé apporte deux contributions essentielles aux données du problème :

une modification des espérances des données aléatoires $({\hat {v}}$ au lieu de ${\bar {v}})$ qui découle du potentiel « explicatif » des variables externes ou exogènes (espérance conditionnelle),
une réduction du sigma de ces données $({\hat {\sigma }}(v)\leqslant \sigma (v))$ dû au caractère projectif de la prévision.

Dans le contexte de l’exemple, le profit espéré du vendeur augmentera s’il peut saisir les relations (régression linéaire par exemple) entre la demande et certaines variables exogènes comme la météo (peu d'acheteurs potentiels s’il pleut), l’intérêt des nouvelles du journal, le type de jour, etc. Un vendeur expérimenté sait interpréter les conditions qui influencent le volume de ses ventes et quantifier intuitivement leurs effets.

Même si, dans un cas particulier où les variables exogènes ne modifient pas l’espérance $({\hat {v}}={\bar {v}})$ , un coefficient de corrélation $R^{2}=0.75$ est suffisant pour réduire $\displaystyle \sigma (v)$ d’un facteur 2. En reprenant les résultats de l’exemple précédent, si $\displaystyle \sigma (v)=$ 20 peut être réduit à 10 grâce à une prévision, le profit espéré augmentera de 20 %.

Voir aussi

Optimisation des stocks

Notes

On obtient ce même résultat en partant de la formulation générale dans laquelle $\rho (v)$ est remplacé par une distribution de Dirac translatée de ${\bar {v}}$ , ce qui implique une répartition cumulative $F(v)$ du type fonction de Heaviside

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.