Accueil🇫🇷Chercher

Polychore de Schläfli-Hess

Les dix polychores de Schläfli-Hess sont les polytopes réguliers étoilés (non convexes) de dimension 4. Analogues aux solides de Kepler-Poinsot de dimension 3, ils s'obtiennent par stellation de l'hécatonicosachore et de l'hexacosichore. Ils furent catalogués par Ludwig Schläfli et Edmund Hess (de) durant la seconde moitié du XIXe siècle.

Polychore Projection orthogonale Symbole de Schläfli Sommets Arêtes Faces Cellules
Hécatonicosachore icosaédral {3,5,5/2} 120 720 1200

(triangles)

 120

(icosaèdre)

Petit hécatonicosachore étoilé 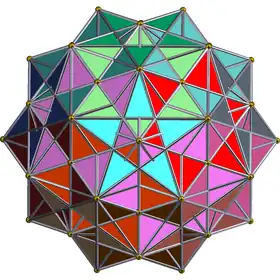{5/2,5,3} 120 1200 720

(pentagrammes)

 120

(petits dodécaèdres étoilés)

Grand hécatonicosachore étoilé {5,5/2,5} 120 720 720

(pentagones)

 120

(grands dodécaèdres)

Hécatonicosachore 5,3,5/2 {5,3,5/2} 120 720 720

(pentagones)

 120

(dodécaèdres)

Hécatonicosachore 5/2,3,5 {5/2,3,5} 120 720 720

(pentagrammes)

 120

(grands dodécaèdres étoilés)

Hécatonicosachore 5/2,5,5/2 {5/2,5,5/2} 120 720 720

(pentagrammes)

 120

(petits dodécaèdres étoilés)

Hécatonicosachore 5,5/2,3 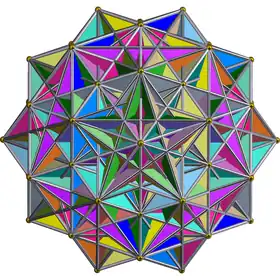{5,5/2,3} 120 1200 720

(pentagones)

 120

(grands dodécaèdres)

Hécatonicosachore 3,5/2,5 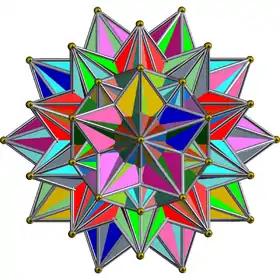{3,5/2,5} 120 720 1200

(triangles)

 120

(grands icosaèdres)

Grand hexacosichore 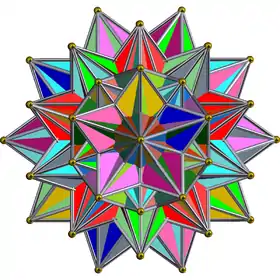{3,3,5/2} 120 720 1200

(triangles)

 600

(tétraèdres)

Hécatonicosachore 5/2,3,3 {5/2,3,3} 600 1200 720

(pentagrammes)

 120

(grands dodécaèdres étoilés)

Voir aussi

4-polytope régulier convexe

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.