Petit hécatonicosachore étoilé
En géométrie, le petit hécatonicosachore étoilé ou polydodécaèdre étoilé est un 4-polytope étoilé régulier ayant pour symbole de Schläfli {5/2,5,3}. C'est l'un des 10 polychores de Schläfli-Hess.
| Petite hécatonicosachore étoilé | |
|---|---|
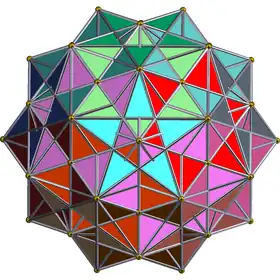 Projection orthogonale Projection orthogonale | |
| Type | Polychore de Schläfli-Hess |
| Cellules | 120 {5/2,5} |
| Faces | 720 {5/2} |
| Arêtes | 1200 |
| Sommets | 120 |
| Figure de sommet | {5,3} |
| Symbole de Schläfli | {5/2,5,3} |
| Diagramme de Coxeter-Dynkin | |
| Groupe de symétrie | H4, [3,3,5] |
| Dual | Hécatonicosachore icosaédral |
| Propriétés | Régulier |
Polytopes associés
Il a la même disposition d'arêtes (en) que l'hécatonicosachore 5,5/2,5 et partage également ses 120 sommets avec l'hexacosichore et huit autres polytopes réguliers étoilés. Il peut également être considéré comme la première stellation de l'hécatonicosichore. En ce sens, il pourrait être considéré comme analogue au petit dodécaèdre étoilé tridimensionnel, qui est la première stellation du dodécaèdre. En effet, le petit 120-cellule étoilé est dual de l'icosaèdre à 120 cellules, qui pourrait être pris comme un analogue 4D du grand dodécaèdre, dual du petit dodécaèdre étoilé.
Articles connexes
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Small stellated 120-cell » (voir la liste des auteurs).
- Edmund Hess, (1883) Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder .
- HSM Coxeter, Polytopes réguliers, 3e. éd., Dover Publications, 1973. (ISBN 0-486-61480-8) .
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, Les symétries des choses 2008, (ISBN 978-1-56881-220-5) (Chapitre 26, Regular Star-polytopes, p. 404-408)