Points isodynamiques

Les points isodynamiques ont été à l'origine définis à partir de certaines égalités de rapports (ou, de façon équivalente, de produits) de distances entre des paires de points. Si S et S' sont les points isodynamiques d'un triangle ABC, alors on a AS × BC = BS × AC = CS × AB. Des égalités analogues sont vérifiées pour le point S'. Neuberg appelle ces points "isodynamiques" en raison de cette propriété[3]. De manière équivalente, les distances AS, BS et CS sont inversement proportionnelles aux longueurs des côtés du triangle BC, AC et AB.

Les points S et S' sont les points d'intersection des trois cercles d'Apollonius associés au triangle ABC, les trois cercles passant par un sommet du triangle et maintenant un rapport de distances constant aux autres sommets[4] - [5]. Ainsi, la droite SS' est l'axe radical des trois paires de cercles d'Apollonius. La médiatrice du segment [SS'] est la droite de Lemoine du triangle, qui passe par les centres des cercles d'Apollonius[6].

Les points isodynamiques S et S' d'un triangle ABC peuvent être définies par leurs propriétés après transformations du plan, et particulièrement les inversions et les transformations de Möbius (produis d'inversions multiples). L'inversion du triangle ABC par rapport à un des points isodynamiques transforme en effet le triangle ABC en un triangle équilatéral[1] - [4]. L'inversion par rapport au cercle circonscrit du triangle ABC laisse le triangle invariant mais envoie un des points isodynamiques sur l'autre[4] - [5].

Plus généralement, les points isodynamiques sont invariants par transformations de Möbius : la paire non ordonnée de points isodynamiques d'une transformation de ABC est égale à la même transformation appliquée à la paire {S , S'}. Plus précisément, les points isodynamiques pris individuellement sont fixes par les transformations de Möbius qui projette l'intérieur du cercle circonscrit de ABC vers l'intérieur du cercle circonscrit du triangle transformé, et permutés par les transformations qui échangent l'intérieur et l'extérieur du cercle circonscrit[7].

Trois cercles, chacun faisant un angle de π/3 avec le cercle circonscrit et les deux autres, se croisent au premier point isodynamique.

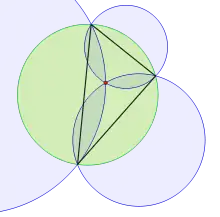
En plus d'être les intersections des cercles d'Apollonius, chaque point isodynamique est le point d'intersection d'un autre triplet de cercles. Le premier point isodynamique est l'intersection de trois cercles passant par les paires de points AB, AC et BC, où chacun des trois cercles croise le cercle circonscrit du triangle ABC pour former une lentille avec un angle au sommet 2π/3. De façon similaire, le deuxième point isodynamique est l'intersection de trois cercles qui croise le cercle circonscrit pour former des lentilles avec un angle au sommet de π/3[7].

Les angles formés par le premier point isodynamique avec les sommets du triangle satisfont les équations ${\displaystyle {\widehat {ASB}}={\widehat {ACB}}+\pi /3}$, ${\displaystyle {\widehat {ASC}}={\widehat {ABC}}+\pi /3}$ et ${\displaystyle {\widehat {BSC}}={\widehat {BAC}}+\pi /3}$. De manière analogue, les angles formés par le deuxième point isodynamique vérifient ${\displaystyle {\widehat {AS'B}}={\widehat {ACB}}-\pi /3}$, ${\displaystyle {\widehat {AS'C}}={\widehat {ABC}}-\pi /3}$ et ${\displaystyle {\widehat {BS'C}}={\widehat {BAC}}-\pi /3}$[7].

Le triangle pédal d'un point isodynamique (le triangle formé en projetant orthogonalement S sur les trois côtés du triangle ABC) est équilatéral[1] - [4] car il est le triangle formé en réfléchissant S de chaque côté du triangle[8]. De tous les triangles équilatéraux inscrits dans le triangle ABC, le triangle pédal du premier point isodynamique est celui d'aire minimale[9].

Les points isodynamiques sont sur l'axe de Brocard du triangle, et sont donc alignés avec le centre du cercle circonscrit au triangle, ainsi que son point de Lemoine.

Les points isodynamiques sont les conjugués isogonaux des deux points isogoniques du triangle, et réciproquement[2] - [6].

Le cercle circonscrit au triangle formé par les points isodynamiques et le centre de gravité du triangle de référence est le cercle de Parry du triangle de référence.

La cubique de Neuberg passe par les deux points isodynamiques[6].

Si un cercle est séparé en trois arcs, le premier point isodynamique du triangle formé par les trois points de séparation est l'unique point dans le cercle tel que chacun des trois arcs a autant de chances d'être atteint par un mouvement brownien partant de ce point. Ainsi, le point isodynamique est le point pour lequel les mesures harmoniques des trois arcs sont égales[10].

Construction du premier point isodynamique à partir du symétrique du triangle de référence et de triangles équilatéraux pointant vers l'intérieur.

Le cercle d'Apollonius par le sommet A du triangle ABC peut être construit en trouvant les deux bissectrices (intérieure et extérieure) des deux angles formées par les droites AB et AC au sommet A, et intersectant les bissectrices avec la droite BC. Le segment entre les deux points d'intersection est le diamètre du cercle d'Apollonius. Les points isodynamiques peuvent être trouvés en construisant deux de ces cercles et en repérant leurs deux points d'intersection[4] - [5].

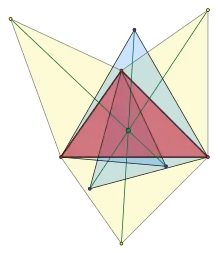
Une autre construction au compas et à la règle graduée implique le symétrique A' du sommet A par la droite BC (l'intersection de cercles centrés en B et C passant par A), et en construisant un triangle équilatéral vers l'intérieur du côté BC du triangle (le sommet A'' de ce triangle est l'intersection de deux cercles avec BC comme rayon). La droite A'A'' croise les droites B'B'' et C'C'', construites de façon similaire, comme le premier point isodynamique. Le deuxième point isodynamique peut être construit de façon similaire mais avec les triangles équilatéraux pointant vers l'extérieur[11].

De façon alternative, la position du premier point isodynamique peut être calculé avec ses coordonnées trilinéaires, qui sont[12]

${\displaystyle \sin(A+\pi /3):\sin(B+\pi /3):\sin(C+\pi /3).}$

Celles du deuxième point isodynamique sont similaires mais avec un angle supplémentaire de -π/3 à la place de π/3.

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Isodynamic point » (voir la liste des auteurs).

• Isodynamic points X(15) and X(16) dans Encyclopedia of Triangle Centers par Clark Kimberling
• (en) Eric W. Weisstein, « Isodynamic Points », sur MathWorld