Lentille (géométrie)
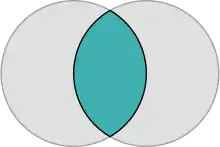
En géométrie euclidienne, une lentille est un ensemble convexe borné par deux arcs de cercle qui se rejoignent à leurs extrémités. Afin que cette forme soit convexe, les deux arcs doivent avoir des courbures inverses (convexe-convexe). Elle peut être vue comme l'intersection de deux disques, ou l'union de deux segments circulaires (régions entre la corde d'un cercle et le cercle lui-même), joint par une corde commune.
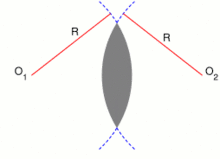
Types
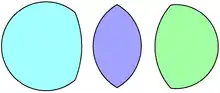
Si les deux arcs ont même rayon, on parle de lentille symétrique, sinon, de lentille asymétrique.
Le vesica piscis est une forme particulière de lentille symétrique, formé par deux arcs de cercle dont le centre d'un arc est sur l'arc opposé. Ils forment donc un angle de 120° à leurs extrémités.
Aire
- Cas symétrique
L'aire d'une lentille symétrique s'exprime en fonction du rayon R et des longueurs d'arc θ en radians :
Cette aire est en effet le double de celle d'un segment circulaire d'angle .
La distance entre les centres des disques est , ce qui donne
Pour le vesica picis, , donc , et , voir la suite A093731 de l'OEIS.
- Cas asymétrique
L'aire d'une lentille asymétrique s'exprime en fonction des rayons R et r et de la distance entre les centres d[1]:
avec
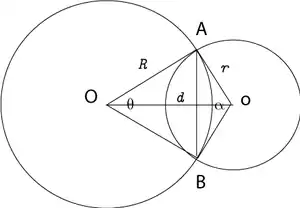
où on reconnait la formule de Héron pour l'aire d'un triangle appliquée à un triangle de côtés d, R et r.
Applications
Le problème de Mrs. Miniver (en), demande la forme d'une lentille symétrique de sorte que son aire soit égale à celle de la différence symétrique des deux disques.
D'après la formule ci-dessus, la longueur d'arc de cette lentille vérifie , soit °, voir la suite A336082 de l'OEIS.
Le rapport , voir la suite A255899 de l'OEIS.
Les lentilles sont utilisées pour définir les bêta squelettes (en), des graphes géométriques définis sur un ensemble de points en connectant des paires de points par un segment partout où une lentille déterminée par deux points est vide.
Voir aussi
.png.webp)
- La lunule, forme non convexe formée par deux arcs circulaires, avec des courbures dans le même sens
- Le problème de la chèvre, dans le cas où l'un des deux cercles est centré sur la circonférence de l'autre.
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Lens (geometry) » (voir la liste des auteurs).
- (en) Eric W. Weisstein, « Lens », sur MathWorld
- Pedoe, D., Circles: A Mathematical View, rev. ed., Washington, DC: Math. Assoc. Amer., (ISBN 978-0883855188)
- Plummer, H., An Introductory Treatise of Dynamical Astronomy, York, Dover, (lire en ligne
 )
) - Watson, G. N., A Treatise on the Theory of Bessel Functions, 2nd ed., Cambridge, England, Cambridge University Press,














