Pavé droit
En géométrie, un pavé droit, ou parallélépipède rectangle[1], est une figure solide délimitée par six faces rectangulaires (boîte rectangulaire).
| Pavé droit Parallélépipède rectangle | |
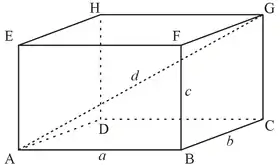 Pavé droit ABCDEFGH avec sa grande diagonale et ses trois dimensions a, b et c | |
| Type | Prisme |
|---|---|
| Faces | 6 rectangles |
| Arêtes | 12 |
| Sommets | 8 |
| Caractéristique | 2 |
| Volume | |
| Aire | |
| Propriétés | convexe, zonoédrique, isogonal |
C'est un parallélépipède dont les trois angles issus d'un sommet sont droits, et tous les angles sont alors droits. Les faces opposées du pavé sont égales. C'est aussi un prisme rectangulaire droit.
Le prisme carré droit[2] (aussi appelé de manière ambiguë prisme carré[3]) est un cas particulier de pavé dont au moins deux faces sont carrées. Le cube est un cas particulier de pavé droit dont toutes les faces sont carrées.
Les arêtes du pavés sont plus souvent appelées ses côtés, et leurs longueurs ses dimensions.
Si les dimensions du pavé sont a, b et c, son volume est le produit abc et son aire est 2(ab + ac + bc).
La longueur de la grande diagonale est d = √a2 + b2 + c2.
Le pavé droit est un polyèdre convexe. Ses six faces bornent une région unique de l'espace. Il possède huit sommets et douze arêtes.
La formule d'Euler F + S = A + 2 (où F est le nombre de faces, S le nombre de sommets et A le nombre d'arêtes d'un polyèdre) donne ici 6 + 8 = 12 + 2.
La forme du pavé droit est souvent utilisée pour les boîtes, les armoires, les pièces, les immeubles, etc. Le pavé droit fait partie des solides pouvant paver un espace tridimensionnel. Cela lui donne une grande polyvalence, puisque chaque pavé droit peut contenir des pavés droits plus petits : une boîte à sucre contient des morceaux de sucre, un immeuble contient des pièces, etc.
Notes et références
- On trouve aussi l'anglicisme "cuboïde", ainsi que l'appellation "brique", dans brique d'Euler.
- Collectif, Dictionnaire technologique, ou Nouveau dictionnaire universel des arts et métiers, et de l'économie industrielle et commerciale, Volume 10, Thomine et Fortic, 1827, p. 282.
- Claude Lucien Bergery, Géométrie des écoles primaires, 1837, p. 135.
Voir aussi
Articles connexes
- Hyperrectangle (en)
- Brique d'Euler
- Tétrèdre équifacial, inscrit dans un pavé droit
- Tétraèdre quadrirectangle, également inscrit dans un pavé droit
Liens externes
- (en) Eric W. Weisstein, « Cuboid », sur MathWorld
- (en) Paper Model of a Rectangular Prism cuboid sur korthalsaltes.com
- (en) Cuboids, Rectangular Prisms and Cubes sur mathsisfun.com
- Volume d’un parallélépipède rectangle sur lememento.fr

