Optimisation quadratique

En optimisation mathématique, un problème d'optimisation quadratique est un problème d'optimisation dans lequel on minimise (ou maximise) une fonction quadratique sur un polyèdre convexe. Les contraintes peuvent donc être décrites par des fonctions linéaires (on devrait dire affines). L'optimisation quadratique est la discipline qui étudie ces problèmes. L'optimisation linéaire peut être vue comme un cas particulier de l'optimisation quadratique.

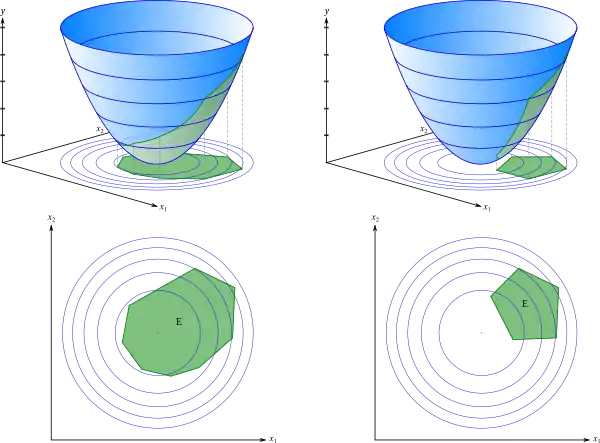
Optimisation quadratique dans un espace à deux dimensions

Optimisation quadratique dans un espace à deux dimensions (x₁, x₂) contraint dans un polygone convexe.

Gauche : l'ensemble admissible E contient le minimum absolu.
Droite : l'ensemble admissible E ne contient pas le minimum absolu.
Haut : vue en perspective.
Bas : vue plane, la valeur de y étant représentée par des courbes de niveau.

Ce problème est NP-difficile dans le cas général. Dans le cas particulier de la minimisation d'une fonction objectif convexe, le problème est polynomial et on parle d'optimisation quadratique convexe ; une discipline déjà très riche aux propriétés mieux connues.

Lorsque le critère et les contraintes du problème d'optimisation sont quadratiques, on parle d'optimisation tout quadratique (en). Cette classe de problèmes contient toute l'optimisation polynomiale et est donc beaucoup plus générale que l'optimisation quadratique.

Formulation du problème

Un problème d'optimisation quadratique consiste à minimiser une fonction quadratique $q:\mathbb {R} ^{n}\to \mathbb {R}$ , non nécessairement convexe, sur un polyèdre convexe.

Critère à minimiser

La fonction $q$ est définie en $x=(x_{1},\ldots ,x_{n})\in \mathbb {R} ^{n}$ par

$q(x)=g^{\mathsf {T}}x+{\frac {1}{2}}\,x^{\mathsf {T}}Hx=\sum _{i=1}^{n}g_{i}x_{i}+{\frac {1}{2}}\,\sum _{i=1}^{n}\sum _{j=1}^{n}H_{ij}x_{i}x_{j}.$

Dans la première expression de $q (x)$ , l'expression sous forme matricielle, $g\in \mathbb {R} ^{n}$ est un vecteur et $H\in \mathbb {R} ^{n\times n}$ est une matrice réelle symétrique (celle-ci est généralement supposée symétrique, car $q$ ne voit pas la partie antisymétrique éventuelle de $H$ ). Il ne sert à rien de garder le terme constant dans $q$ , car celui-ci n'affecte pas la solution du problème de minimisation.

Rappelons qu'une telle fonction quadratique $q$ est

convexe si, et seulement si, la matrice $H$ est semi-définie positive,
strictement convexe si, et seulement si, la matrice $H$ est définie positive.

Contraintes

On impose également au vecteur recherché $x$ d'appartenir à un polyèdre convexe, ce qui revient à dire que $x$ doit vérifier un nombre fini de contraintes affines. Celles-ci peuvent prendre des formes variées comme

${\begin{array}{ll}l_{B}\leqslant x\leqslant u_{B}&{\mbox{(contraintes de borne)}}\\l_{I}\leqslant A_{I}x\leqslant u_{I}&{\mbox{(contraintes d'inégalité affines)}}\\A_{E}x=b_{E}&{\mbox{(contraintes d'égalité affines),}}\end{array}}$

expressions dans lesquelles on a noté

$l B$ et $u B$ des vecteurs de ${\bar {\mathbb {R} }}^{n}$ pouvant donc prendre des valeurs infinies et vérifiant $l B < u B$ ,
$A_{I}\in \mathbb {R} ^{m_{I}\times n}$ une matrice réelle de type $m I \times n$ ( $A I x$ désigne le produit de la matrice $A I$ par le vecteur $x$ ),
$l I$ et $u I$ des vecteurs de ${\bar {\mathbb {R} }}^{m_{I}}$ pouvant donc prendre des valeurs infinies et vérifiant $l I < u I$ ,
$A_{E}\in \mathbb {R} ^{m_{E}\times n}$ une matrice réelle de type $m E \times n$ ,
$b_{E}\in \mathbb {R} ^{m_{E}}$ un vecteur réel.

Il sera intéressant d'utiliser la notation compacte

$[l_{B},u_{B}]:=\{x\in \mathbb {R} ^{n}:l_{B}\leqslant x\leqslant u_{B}\}$

et une définition similaire pour $[l I, u I]$ . On note $X Q$ l'ensemble admissible défini par toutes les contraintes ci-dessus, à savoir

$X_{Q}:=\{x\in \mathbb {R} ^{n}:x\in [l_{B},u_{B}],~A_{I}x\in [l_{I},u_{I}],~A_{E}x=b_{E}\}.$

Formulation compacte

De manière compacte, on peut donc écrire le problème d'optimisation quadratique de la manière suivante

$(P_{Q})\quad \inf _{x\in X_{Q}}\,q(x).$

On dit que ce problème est convexe si le critère $q$ est convexe, ce qui est le cas si, et seulement si, $H$ est semi-définie positive.

Analyse du problème

Existence de solution

Le résultat fondamental est dû à Frank et Wolfe (1956[1]). Il est du même type que celui connu en optimisation linéaire. Rappelons que

un problème d'optimisation est dit réalisable si son ensemble admissible est non vide (ce qui revient à dire que sa valeur optimale ne vaut pas $+\infty$ ),
un problème d'optimisation réalisable est dit borné si sa valeur optimale ne vaut pas $-\infty$ (on ne peut pas trouver une suite de points admissibles faisant tendre le critère vers $-\infty$ ).

Existence de solution — Pour un problème d'optimisation quadratique (non nécessairement convexe), les propriétés suivantes sont équivalentes :

le problème a une solution,
le problème est réalisable et borné,
la valeur optimale du problème est finie.

L'unicité de la solution aura certainement lieu si $q$ est strictement convexe, mais pourra se produire sans cela. C'est le cas par exemple pour le problème à une unique variable $inf{x : x \geq 0}$ , dont le critère est linéaire (donc pas strictement convexe).

Bornitude

Voici une caractérisation du caractère borné (ou non borné) d'un problème quadratique convexe réalisable (c'est-à-dire dont l'ensemble admissible est non vide) en termes d'existence d'une direction qui a des intérêts théorique et numérique[2]. On y a noté $X \infty$ le cône asymptotique de l'ensemble $X$ .

Bornitude d'un problème quadratique convexe — Pour un problème d'optimisation quadratique convexe réalisable, dont l'ensemble admissible polyédrique est noté $X$ , les propriétés suivantes sont équivalentes :

le problème est non borné,
il existe une direction $d$ telle que $g^{\top }d<0$ , $Hd=0$ et $d\in X^{\infty }$ .

Le cône asymptotique de l'ensemble admissible $X Q$ défini ci-dessus (supposé non vide) s'écrit

$X_{Q}^{\infty }=\{d\in \mathbb {R} ^{n}:d\in [l_{B},u_{B}]^{\infty },~A_{I}d\in [l_{I},u_{I}]^{\infty },~A_{E}d=0\}.$

L'expression de $[l, u] \infty$ est donnée dans la page sur le cône asymptotique.

Méthodes de résolution

S'il n'y a que des contraintes d'égalité, le problème revient à résoudre un système linéaire. En présence de contraintes d'inégalité, le problème en général est NP-ardu et peut être résolu par les approches suivantes :

Algorithme d'activation,
Algorithme du gradient conjugué (des extensions),
Algorithme du gradient projeté,
Algorithme du lagrangien augmenté[3],
Méthode de Nelder-Mead (des extensions).
Algorithmes de points intérieurs (pour problème convexe).

Annexes

Note

Voir l'appendice (i) de l'article.
Voir par exemple le lemme 2.2 dans l'article de Chiche et Gilbert (2014).
Beaucoup de contributions sur ce sujet. L'article de Delbos et Gilbert (2005) en analyse la convergence linéaire globale lorsque le problème a une solution; celui de Chiche et Gilbert (2014) en analyse le comportement lorsque le problème n'est pas réalisable.

Lien externe

Operations Research Models and Methods (Paul A. Jensen and Jonathan F. Bard)

Bibliographie

(en) A. Chiche, J. Ch. Gilbert (2016). How the augmented Lagrangian algorithm can deal with an infeasible convex quadratic optimization problem. Journal of Convex Analysis, 23:2, 425-459.
(en) F. Delbos, J. Ch. Gilbert (2005). Global linear convergence of an augmented Lagrangian algorithm for solving convex quadratic optimization problems. Journal of Convex Analysis, 12, 45–69.
(en) M. Frank, P. Wolfe (1956). An algorithm for quadratic programming. Naval Research Logistics Quarterly, 3, 95–110.

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.