Méthode de Nelder-Mead
La méthode de Nelder-Mead est un algorithme d'optimisation non linéaire qui a été publiée[1] par John Nelder et Roger Mead (en) en 1965. C'est une méthode numérique heuristique qui cherche à minimiser une fonction continue dans un espace à plusieurs dimensions.
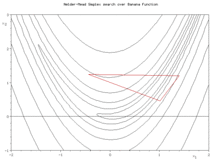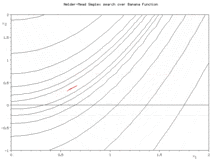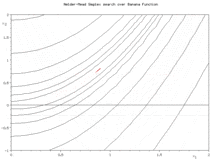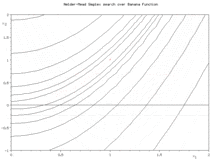
Appelée également downhill simplex method, l’algorithme exploite le concept de simplexe qui est un polytope de N+1 sommets dans un espace à N dimensions. Partant initialement d’un tel simplexe, celui-ci subit des transformations simples au cours des itérations : il se déforme, se déplace et se réduit progressivement jusqu’à ce que ses sommets se rapprochent d’un point où la fonction est localement minimale.
La méthode de Nelder-Mead avec recuit simulé est issue du couplage entre l’algorithme d’origine et le mécanisme empirique du recuit simulé.
Algorithme
Soit une fonction f définie sur un espace de dimension N. L'algorithme débute par la définition d'un simplexe non dégénéré choisi dans cet espace. Par itérations successives, le processus consiste à déterminer le point du simplexe où la fonction est maximale afin de le remplacer par la réflexion (c'est-à-dire le symétrique) de ce point par rapport au centre de gravité des N points restants. Si la valeur de la fonction en ce nouveau point est inférieure à toutes les autres valeurs prises sur les autres points, le simplexe est étiré dans cette direction. Sinon si la valeur de la fonction en ce nouveau point est meilleure que la deuxième moins bonne mais moins bonne que la meilleure, on garde cette valeur et on recommence. Sinon, il est supposé que l'allure locale de la fonction est une vallée, et le simplexe est contracté sur lui même. Si cela ne donne toujours pas un meilleur point, le simplexe est réduit par une homothétie centrée sur le point du simplexe où la fonction est minimale.
Plus précisément :
- Choix de N+1 points de l'espace des inconnues de dimension N. Cela forme un simplexe : {},
- Calcul des valeurs de la fonction f en ces points, tri des points de façon à avoir . Il suffit en fait de connaître le premier et les deux derniers.
- Calcul de x0, centre de gravité de tous les points sauf xN+1.
- Calcul de (réflexion de xN+1 par rapport à x0).
- Soit , remplacement de xN+1 par et retour à l'étape 2.
- Soit , calcul de (expansion du simplexe). Si , remplacement de xN+1 par sinon, remplacement de xN+1 par xr et retour à l'étape 2.
- Soit , calcul de (contraction du simplexe). Si , remplacement de xN+1 par xc et retour à l'étape 2, sinon aller à l'étape 8.
- Homothétie de rapport et de centre x1 : remplacement de xi par et retour à l'étape 2.
Avec des coefficients tels que , et . Des valeurs standards sont , , et .
Analyse
Avantages
- La généralité : la méthode s'applique à une fonction continue sans avoir à évaluer ses dérivées.
- La simplicité de la mise en œuvre.
- L’efficacité pour une fonction non dérivable.
- L’interprétation géométrique sous-jacente.
- Assurance d’obtenir une série décroissante de valeurs.
Inconvénients
- S’applique mal (ou difficilement) lorsque le domaine de définition de la fonction est complexe ou que le minimum recherché se situe dans un voisinage de la frontière.
- Elle nécessite la donnée « arbitraire » d’un simplexe de départ, qui peut ralentir l’algorithme si mal choisi.
- Une dégradation des performances lorsque la dimension N augmente.
- Le risque que les simplexes obtenus successivement aient tendance à dégénérer (bien que l’expérience montre que ce soit rarement le cas).
- L'optimum obtenu par la méthode n'est pas forcément un optimum global.
Amélioration facile et très efficace : redémarrer l'algorithme
Pour pallier les inconvénients 1) et 4), ainsi que d'autres, le fait de redémarrer l'algorithme de Nelder-Mead à partir de la dernière solution obtenue (et continuer de le redémarrer jusqu'à ce qu'il n'y ait plus d'amélioration, jusqu'à une précision donnée) ne peut qu'améliorer (parfois très fortement) la solution finale[2] - [3]. De même, il est souvent conseillé de faire plusieurs exécutions de l'algorithme, à partir de solutions initiales différentes (là encore, pour diminuer l'impact des inconvénients de la méthode et permettre de trouver une meilleure solution finale).
Lorsque le domaine de définition admet une frontière et que le minimum se situe sur ou à proximité de cette frontière, les déformations successives du simplex ont tendance à le dégénérer. Une manière efficace de l'éviter consiste à prolonger la fonction hors de sa frontière en lui ajoutant une pénalité.
Méthode de Nelder-Mead avec recuit simulé
Lorsque la fonction possède de nombreux minima locaux, il arrive fréquemment de converger vers l’un d’eux et de manquer la solution. Dans un tel cas, il est possible d’introduire[4] dans la méthode de Nelder-Mead un couplage avec le mécanisme empirique du recuit simulé : à chaque itération, les valeurs effectives de la fonction aux divers sommets sont perturbées par un bruit de fond « thermique » aléatoire dont l’importance décroît au fur et à mesure que l’algorithme progresse.
Notes et références
- (en) John Nelder et Roger Mead, « A simplex method for function minimization », Computer Journal, vol. 7, no 4, , p. 308-313
- « Improving the convergence of Nelder-Mead (and so fminsearch) », sur Mathworks.com (consulté le ).
- Simon, Emile, « Optimal static output feedback design through direct search », sur arXiv.org, (consulté le ).
- W. H Press, S. A. Teukolsky, W. T. Vetterling, B. P. Flannery, « Numerical Recipes : The Art of Scientific Computing », Cambridge University Press, Third Edition (2007)





















