Octogramme
En géométrie, un octogramme ou étoile à huit branches est un polygone étoilé à huit angles.
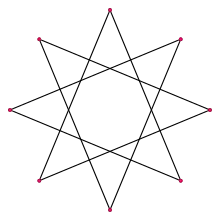
Le nom octogramme combine le préfixe numérique grec, octo-, avec le suffixe -gram . Le suffixe -gram dérive de γραμμή (grammḗ) signifiant "ligne"[1].
Détail
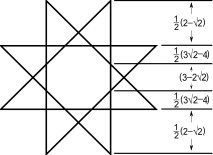
En général, un octogramme est n'importe quel octogone dont les arêtes s'intersectent.
L'octogramme régulier est dénoté par le symbole Schläfli {8/3}, qui signifie une étoile à 8 côtés, reliée un point sur trois.
Variantes
Ces variations ont une symétrie plus faible, à savoir D4 :
  (rotation à 45 degrés) |
  Isotoxal |
 Ancien drapeau du Chili (le Guñelve). |
 L'étoile octogonale régulière est très populaire en tant que symbole des clubs d'aviron en Cologne (drapeau du club de l'Association d'aviron de Cologne) |
 La géométrie peut être ajustée pour que 3 arêtes se croisent en un seul point, comme le symbole d'Auseklis |
 Une rose des vents à 8 points peut être considérée comme une étoile octogonale, avec 4 points principaux et 4 points secondaires. |
Composés de polygones étoilés
Il y a deux étoiles octogrammiques régulières (composées) de la forme {8/k}, la première construite comme deux carrés {8/2}=2{4}, et la seconde comme quatre digones dégénérés, {8/4}=4{2}. Il existe d'autres composés isogonaux et isotoxaux.
| Régulier | Isogonal | Isotoxal | ||
|---|---|---|---|---|
.svg.png.webp) a{8}={8/2}=2{4} a{8}={8/2}=2{4} |
.svg.png.webp) {8/4}=4{2} {8/4}=4{2} |
 |
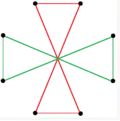 |
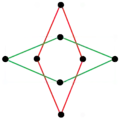 |
{8/2} ou 2{4}, comme les diagrammes de Coxeter ![]()
![]()
![]() +
+![]()
![]()
![]() , peut être vu comme l'équivalent 2D du composé 3D du cube et de l'octaèdre,
, peut être vu comme l'équivalent 2D du composé 3D du cube et de l'octaèdre, ![]()
![]()
![]()
![]()
![]() +
+![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() , ou
, ou ![]()
![]()
![]()
![]()
![]()
![]()
![]() +
+![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Autres présentations d'une étoile octogonale
Une étoile octogonale peut être vue comme un hexadécagone concave, sans intersections intérieures.
| Polygone étoilé | Concave | Découpages | ||
|---|---|---|---|---|
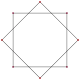 Composé de 2{4} Composé de 2{4} |
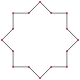 |8/2| |8/2| |
 |
 |
 |
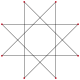 {8/3} {8/3} |
 |8/3| |8/3| |
 |
 |
 |
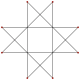 Isogonal Isogonal |
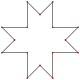 |
 |
 |
 |
 Isotoxal Isotoxal |
 |
 |
 |
 |
Articles connexes
- Usage
- Rub el Hizb – caractère islamique
- Étoile d'Ishtar (en) - symbole de l'ancienne déesse sumérienne Inanna et de son homologue orientale Ishtar, et de la Vénus romaine.
- Étoile de Lakshmi - caractère indien
- Rose des vents - utilisation dans les boussoles pour représenter les directions cardinales des huit vents principaux
- Auseklis (en) - utilisation de l'octagramme régulier par les Lettons
- Guñelve (en) – représentation de Vénus dans l'iconographie mapuche.
- Selburose - blason norvégien
- Étoiles en général
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Octagram » (voir la liste des auteurs).
- γραμμή, Henry George Liddell, Robert Scott, A Greek-English Lexicon, on Perseus
- Grünbaum, B. et GC Shephard ; Carrelage et motifs, New York : WH Freeman & Co., (1987), (ISBN 0-7167-1193-1) .
- Grünbaum, B. ; Polyèdres à faces creuses, Proc de la conférence NATO-ASI sur les polytopes...etc. (Toronto 1993), éd. T. Bisztriczky et al., Kluwer Academic (1994) p. 43-70.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, Les symétries des choses 2008, (ISBN 978-1-56881-220-5) (Chapitre 26. p. 404 : Polytopes étoilés réguliers Dimension 2)
Liens externes
- (en) Eric W. Weisstein, « Octagramme », sur MathWorld