Nombre presque entier

Des exemples de nombres presque entiers sont les puissances entières élevées du nombre d'or ${\displaystyle \varphi }$. Pour mémoire :

${\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}\simeq 1{,}618\dots }$.

On a par exemple :

${\displaystyle \varphi ^{17}=3571{,}000280\dots }$

${\displaystyle \varphi ^{18}=5777{,}999827\dots }$

${\displaystyle \varphi ^{19}=9349{,}000107\dots }$

${\displaystyle \varphi ^{20}=15126{,}999934\dots }$

${\displaystyle \varphi ^{21}=24476{,}000040\dots }$

${\displaystyle \varphi ^{22}=39602{,}999974\dots }$.

Le fait que ces valeurs s'approchent de nombres entiers s'explique du fait que le nombre d'or est un nombre de Pisot-Vijayaraghavan : un entier algébrique réel strictement supérieur à 1 dont les éléments conjugués (ici : ${\displaystyle -1/\varphi }$) sont en module strictement inférieurs à 1. Il en résulte que pour ${\displaystyle n\gg 1}$ :

${\displaystyle \varphi ^{n}\approx L_{n}-{\frac {(-1)^{n}}{L_{n}}}}$

où L_n est le n-ième nombre de Lucas.

Une proportion importante des premiers nombres de la forme ${\displaystyle \mathrm {e} ^{\pi {\sqrt {n}}}}$ ont une partie décimale commençant par plusieurs 9 :

${\displaystyle \mathrm {e} ^{\pi {\sqrt {6}}}={\text{entier}}+0{,}99\dots }$

${\displaystyle \mathrm {e} ^{\pi {\sqrt {17}}}={\text{entier}}+0{,}99\dots }$

${\displaystyle \mathrm {e} ^{\pi {\sqrt {18}}}={\text{entier}}+0{,}99\dots }$

${\displaystyle \mathrm {e} ^{\pi {\sqrt {22}}}={\text{entier}}+0{,}99\dots }$

${\displaystyle \mathrm {e} ^{\pi {\sqrt {25}}}={\text{entier}}+0{,}999\dots }$

${\displaystyle \mathrm {e} ^{\pi {\sqrt {37}}}={\text{entier}}+0{,}9999\dots }$

${\displaystyle \mathrm {e} ^{\pi {\sqrt {43}}}={\text{entier}}+0{,}999\dots }$

${\displaystyle \mathrm {e} ^{\pi {\sqrt {58}}}={\text{entier}}+0{,}999999\dots }$

${\displaystyle \mathrm {e} ^{\pi {\sqrt {59}}}={\text{entier}}+0{,}99\dots }$

${\displaystyle \mathrm {e} ^{\pi {\sqrt {67}}}={\text{entier}}+0{,}99999\dots }$

${\displaystyle \mathrm {e} ^{\pi {\sqrt {74}}}={\text{entier}}+0{,}999\dots }$

${\displaystyle \mathrm {e} ^{\pi {\sqrt {163}}}={\text{entier}}+0{,}99999999999925\dots }$

${\displaystyle \mathrm {e} ^{\pi {\sqrt {232}}}={\text{entier}}+0{,}99999\dots }$

${\displaystyle \mathrm {e} ^{\pi {\sqrt {719}}}={\text{entier}}+0{,}9999\dots }$

${\displaystyle \mathrm {e} ^{\pi {\sqrt {1169}}}={\text{entier}}+0{,}9999\dots }$

${\displaystyle \mathrm {e} ^{\pi {\sqrt {1467}}}={\text{entier}}+0{,}99999999\dots }$

${\displaystyle \mathrm {e} ^{\pi {\sqrt {4075}}}={\text{entier}}+0{,}99999\dots }$

${\displaystyle \mathrm {e} ^{\pi {\sqrt {5773}}}={\text{entier}}+0{,}9999\dots }$.

En supposant que la partie décimale ait une répartition uniforme entre 0 et 1, on s'attendrait à observer statistiquement, parmi les nombres ${\displaystyle \mathrm {e} ^{\pi {\sqrt {n}}}}$ :

• un nombre (au lieu des onze observés) dont la partie décimale commence par 0,99..., pour 1 ≤ n < 100 ;
• un nombre (au lieu des neuf observés) dont la partie décimale commence par 0,999..., pour 1 ≤ n < 1 000 ;
• un nombre (au lieu des dix observés) dont la partie décimale commence par 0,9999..., pour 1 ≤ n < 10 000.

Logarithme de la distance de e^nπ√x à l'entier le plus proche en fonction de n pour x = 163, 58 et 67.

Le nombre ${\displaystyle \mathrm {e} ^{\pi {\sqrt {163}}}}$, qui est le plus étonnant, est parfois nommé constante de Ramanujan[1], à cause de l'anecdote suivante : en 1975, Martin Gardner proposa dans la revue Scientific American un poisson d'avril, dans lequel il prétendait que ce nombre était un entier (à la précision des ordinateurs de l'époque) et que cela avait été prédit par le mathématicien indien Ramanujan. En réalité, on savait depuis 1934 que les nombres de cette forme sont non seulement non entiers, mais transcendants (c'est une conséquence du théorème de Gelfond-Schneider) ; d'autre part, en utilisant des développements en série liés aux formes modulaires[2], Ramanujan avait effectivement remarqué[3] d'autres nombres presque entiers, comme e^π√58, mais cette propriété pour e^π√163 avait été mentionnée par Charles Hermite dès 1859[4] - [5].

Autre fait remarquable : trois des nombres de la liste correspondent aux valeurs de n qui sont les trois plus grands nombres de Heegner : 43, 67 et 163. On a :

${\displaystyle {\begin{aligned}\mathrm {e} ^{\pi {\sqrt {43}}}&\approx 12^{3}(9^{2}-1)^{3}+744-0{,}00022\\\mathrm {e} ^{\pi {\sqrt {67}}}&\approx 12^{3}(21^{2}-1)^{3}+744-0{,}0000013\\\mathrm {e} ^{\pi {\sqrt {163}}}&\approx 12^{3}(231^{2}-1)^{3}+744-0{,}00000000000075.\end{aligned}}}$

La présence des carrés (de 9, 21 et 231) est en relation avec certaines séries d'Eisenstein[6].

Les puissances de la constante de Ramanujan sont également des nombres presque entiers, quoique de moins en moins au fur et à mesure que l'exposant augmente :

e^π√163 = 262537412640768743,99999999999925...

e^2π√163 = 68925893036109279891085639286943768,00000000016...

e^3π√163 = 18095625621654510801615355531263454706630064771074975,9999999901...

e^4π√163 = 4750778730825177725463920948909726618214491718039471366318747406368792,00000030...

e^5π√163 = 1247257156019637304856107520018074552566824585862995272173368815794085495792299621093743,9999936...

e^6π√163 = 327451666639079200503292535866541250265248788274691526825971156747731856100971255480468836963064283775072,000097...

e^7π√163 = 85968313324331384516193000468092278329755548797409399442004776269126859976027905282083513810327974584994948290745606149951,9988...

e^8π√163 = 22569898549260886473888468331565301907474037192863812586061996691592154447956371062753799948390245371838040419276512345203199926422461218840,012....

Le fait que ces puissances soient elles aussi des nombres presque entiers est une coïncidence supplémentaire, elle ne découle pas du fait que la constante de Ramanujan soit un nombre presque entier (la différence entre le carré du nombre entier proche de e^π√163 et le nombre entier proche de e^2π√163 est de 393 768).

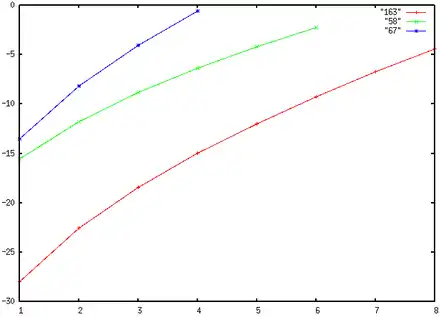
Par ailleurs, ces puissances sont proches d'un entier alternativement par en dessous (exposants impairs) et par en dessus (exposants pairs). Enfin, la courbe représentant le logarithme de la distance de la puissance n-ième à l'entier le plus proche est remarquablement régulière de la puissance 1 à la puissance 8 (voir la figure ci-dessus).

Ceci s'observe également mais dans une moindre mesure pour les puissances de e^π√58 (approximations toutes par en dessous) :

e^π√58 = 24591257751,99999982...

e^2π√58 = 604729957825300084759,9999921...

e^3π√58 = 14871070263238043663567627879007,99984...

e^4π√58 = 365698321891389219219142531076638716362775,9982...

e^5π√58 = 8992981693105016374155646905045678991816481660068751,984...

et pour les puissances de e^π√67 :

e^π√67 = 147197952743,9999986...

e^2π√67 = 21667237292024856735768,00029...

e^3π√67 = 3189372971004509360884026494978975,982....

${\displaystyle \left({\frac {\ln(640320^{3}+744)}{\pi }}\right)^{2}=163{,}\underbrace {0000000000000000000000000000} _{28}232\dots }$.

François Le Lionnais cite[7] ce cas (qui n'est d'ailleurs qu'une variante de la constante de Ramanujan) comme étant « certainement l'approximation la plus étonnante d'un entier dans l'univers ».

Pourtant, l'approximation suivante, avec trente et un zéros après la virgule[8], dépasse ce record :

${\displaystyle \sum _{n=1}^{\infty }{\frac {n^{3}}{\mathrm {e} ^{2\pi n/13}-1}}=119{,}\underbrace {0000000000000000000000000000000} _{31}959374585\dots }$ ;

on trouvera des approximations plus précises encore, découvertes récemment par ordinateur, dans l'article « Mathématiques expérimentales ».

Des nombres presque entiers utilisant les constantes π et e ont souvent étonné et amusé les mathématiciens. Par exemple :

${\displaystyle \mathrm {e} ^{\pi }-\pi =19{,}999099979\dots }$ ;

${\displaystyle \pi ^{\sqrt[{3}]{93}}-\mathrm {e} ^{\sqrt[{3}]{93}}=86{,}0000188811\dots }$ ;

${\displaystyle \left|\pi ^{\mathrm {e} \,\mathrm {i} }-1\right|=1{,}99977658827\dots }$.

Coïncidence mathématique

• (en) Eric W. Weisstein, « Almost Integer », sur MathWorld
• (en) J. S. Markovitch, « Coincidence, data compression, and Mach's concept of economy of thought », sur cogprints.org, 2004