Méthodes de calcul d'intégrales de contour

Les contours sont définis comme des courbes régulières orientées[6]. On peut ainsi définir précisément un "morceau" d'une courbe lisse, dont on trace un contour.

Une courbe lisse est une fonction z : [a, b] → C avec une dérivée continue qui ne s'annule pas et ne possèdent pas de point double, sauf peut-être aux extrémités (tel que z(a) = z(b)). On parle alors de courbe fermée, et la fonction doit alors être bijective et les dérivées doivent correspondre aux extrémités (z′(a) = z′(b)). Sinon, on parle d'arc lisse ou de courbe ouverte[6].

La paramétrisation d'une courbe donne un ordre naturel des points de la courbe : z(x) est avant z(y) si x < y. On peut ainsi définir une courbe lisse orientée, ce qui est surtout utile pour les courbes indépendantes d'une paramétrisation spécifique. Ceci peut être fait en considérant des classes d'équivalence de courbes lisses avec la même direction. Une courbe lisse orientée est alors un ensemble ordonné de points du plan complexe, image d'une courbe lisse dans leur ordre naturel (selon la paramétrisation). Il faut noter que tous les ordres de points correspondent à l'ordre naturel d'une courbe lisse. En effet, une courbe lisse donnée n'a que deux ordres. De plus, une courbe fermée peut avoir tout point comme extrémité, alors qu'un arc lisse aura deux possibilités.

Les contours sont les classes de courbes sur lesquelles on peut définir l'intégration de contour. Un contour est une courbe orientée qui est formé d'une suite finie de courbes lisses dirigées dont les extrémités sont reliées pour donner une seule direction. Cela nécessite que la suite de courbes γ₁, …, γ_n soit telle que, le point final de γ_i coïncide avec le point initial de γ_i+1, ∀ i, 1 ≤ i < n. Cela inclut toutes les courbes lisses dirigées. De même, un point singleton du plan complexe peut être considéré comme un contour. Le symbole + est souvent utilisé pour désigner le raccordement des courbes afin de former une nouvelle courbe. Ainsi on peut construire un contour Γ qui est formé de n courbes telles que

$${\displaystyle \Gamma =\gamma _{1}+\gamma _{2}+\cdots +\gamma _{n}.}$$

Pour définir l'intégrale de contour dans ce cas, on dit d'abord considérer l'intégrale, sur une variable réelle, d'une fonction à valeurs complexes. Soit f : R → C une fonction à valeurs complexes d'une variable réelle t. Les parties réelles et imaginaires de f sont souvent dénotées u(t) et v(t), respectivement, de sorte que

$${\displaystyle f(t)=u(t)+\mathrm {i} v(t).}$$

Alors l'intégrale de f sur l'intervalle [a, b] est donnée par

$${\displaystyle {\begin{aligned}\int _{a}^{b}f(t)\,\mathrm {d} t&=\int _{a}^{b}\left(u(t)+\mathrm {i} v(t)\right)\,\mathrm {d} t\\&=\int _{a}^{b}u(t)\,\mathrm {d} t+\mathrm {i} \int _{a}^{b}v(t)\,\mathrm {d} t.\end{aligned}}}$$

Soit f : C → C une fonction continue sur une courbe lisse orientée γ. Soit z : R → C une paramétrisation de γ consistante avec sa direction. Alors l'intégrale le long de γ est notée

$${\displaystyle \int _{\gamma }f(z)\,\mathrm {d} z\,}$$

et se calcule par[6]

$${\displaystyle \int _{\gamma }f(z)\,\mathrm {d} z=\int _{a}^{b}f\left(\gamma (t)\right)\gamma '(t)\,\mathrm {d} t.}$$

Cette définition est bien définie. Ainsi, le résultat est indépendant de la paramétrisation choisie[6]. Dans le cas où l'intégrale à droite n'existe pas, l'intégrale le long de γ n'est pas définie.

La généralisation de l'intégrale de Riemann aux fonctions d'une variable complexe est faite par analogie avec les fonctions d'une variable réelle. La partition d'une courbe lisse orientée γ est définie comme un ensemble de points ordonnés et fini sur γ. L'intégrale sur la courbe est la limite des sommes finies de valeurs de fonction, prise aux points de la partition, où la limite est celle où la distance maximum entre n'importe lequel des deux points successifs sur la partition (dans le plan complexe 2D), connu comme le maillage, tend vers zéro.

Arc de Jordan

Un arc de Jordan est une courbe fermée simple du plan complexe qui sépare le plan en deux parties : l'intérieur et l'extérieur. Les contours les plus simples et intuitifs pour les intégrales de contour sont les arcs de Jordan et les lacets. Afin de pouvoir appliquer le théorème des résidus, on construira donc un lacet entourant les pôles de l'intégrande.

Contour de Hankel

Un contour de Hankel, parcouru dans le sens positif.

Une version totalement linéaire du contour de Hankel.

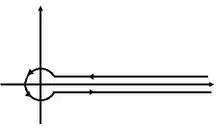
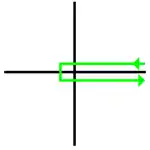
Un contour de Hankel est une courbe ouverte entourant un demi-axe du plan.

La version la plus courante consiste en deux demi-droites parallèles au demi-axe choisi, reliées par un arc de cercle centré à l'origine du demi-axe. Il est parcouru dans le sens horaire.

Ce type de contour est utilisé lorsqu'un logarithme complexe est impliqué, comme la fonction Gamma d'Euler sur le plan complexe.

Contour de Pochhamer

Un contour de Pochhammer tourne dans le sens horaire autour d'un point, puis dans le sens horaire autour d'un autre point, puis dans le sens anti-horaire autour du premier point, et enfin dans le sens anti-horaire autour du second point. La position exacte, la courbure, etc. ne sont pas essentielles dans ce cas, seule la suite de tours importe.

Un contour de Pochhammer, introduit par Camille Jordan[7] et Leo Pochhammer, est utile pour les intégrales de contour autour de deux points. En notant C_A et C_B les boucles parcourues autour des points A et B respectivement, alors le contour de Pochhammer est ABA⁻¹B⁻¹, où l'exposant −1 désigne un chemin parcouru dans le sens inverse.

Par sa construction, la courbe est homologue à 0 mais pas homotopique à 0. Son indice autour de tout point est de 0 malgré le fait qu'à l'intérieur le plan doublement épointé il ne peut pas être réduit à un seul point.

Un cycle de Pochhammer est homologue à zero : c'est la frontière de la surface verte moins la frontière de la rouge.

Un résultat fondamental en analyse complexe est que l'intégrale de contour de 1/z vaut 2πi, avec un chemin pris sur le cercle unité dans le sens anti-horaire (ou toute courbe de Jordan orientée positivement autour de 0). Dans le cas du cercle unité, il y a une méthode directe de calcul de l'intégrale

$${\displaystyle \oint _{C}{\frac {1}{z}}\,\mathrm {d} z.}$$

Dans le calcul de cette intégrale, le cercle unité est caractérisé par |z| = 1, qu'on paramètre par z(t) = e^it, avec t ∈ [0, 2π], ce qui donne dz/dt = ie^it, d'où

$${\displaystyle \oint _{C}{\frac {1}{z}}\,\mathrm {d} z=\int _{0}^{2\pi }{\frac {1}{\mathrm {e} ^{\mathrm {i} t}}}\mathrm {ie} ^{\mathrm {i} t}\,\mathrm {d} t=\mathrm {i} \int _{0}^{2\pi }1\,\mathrm {d} t=\mathrm {i} \,t{\Big |}_{0}^{2\pi }=\left(2\pi -0\right)\mathrm {i} =2\pi \mathrm {i} .}$$

On retrouve bien la valeur attendue.

Illustration du chemin utilisé dans l'exemple.

On considère l'intégrale

$${\displaystyle \int _{-\infty }^{\infty }{\frac {1}{\left(x^{2}+1\right)^{2}}}\,\mathrm {d} x,}$$

Pour le calcul, on passe par la fonction d'une variable complexe

$${\displaystyle f(z)={\frac {1}{\left(z^{2}+1\right)^{2}}}}$$

qui présente deux singularités en i et −i. On choisit donc un contour qui contient l'intégrale réelle, par exemple un demi-cercle dont le diamètre est formé par un intervalle sur la droite réelle (allant de −a vers a, pour a réel strictement supérieur à 1) conviendrait. On note ce contour C.

Il y a deux façons de procéder, selon le théorème qu'on souhaite utiliser :

Avec la formule intégrale de Cauchy

On note que :

$${\displaystyle \oint _{C}f(z)\,\mathrm {d} z=\int _{-a}^{a}f(z)\,\mathrm {d} z+\int _{\text{Arc}}f(z)\,\mathrm {d} z}$$

soit

$${\displaystyle \int _{-a}^{a}f(z)\,\mathrm {d} z=\oint _{C}f(z)\,\mathrm {d} z-\int _{\text{Arc}}f(z)\,\mathrm {d} z.}$$

On observe que

$${\displaystyle f(z)={\frac {1}{\left(z^{2}+1\right)^{2}}}={\frac {1}{(z+\mathrm {i} )^{2}(z-\mathrm {i} )^{2}}}.}$$

Comme la seule singularité contenue dans le contour est celle en i, on peut écrire

$${\displaystyle f(z)={\frac {\frac {1}{(z+\mathrm {i} )^{2}}}{(z-\mathrm {i} )^{2}}},}$$

ce qui donne la fonction sous une forme qui permet l'application directe de la formule intégrale de Cauchy :

$${\displaystyle \oint _{C}f(z)\,\mathrm {d} z=\oint _{C}{\frac {\frac {1}{(z+\mathrm {i} )^{2}}}{(z-\mathrm {i} )^{2}}}\,\mathrm {d} z=2\pi \mathrm {i} \,\left.{\frac {\mathrm {d} }{\mathrm {d} z}}{\frac {1}{(z+\mathrm {i} )^{2}}}\right|_{z=\mathrm {i} }=2\pi \mathrm {i} \left[{\frac {-2}{(z+\mathrm {i} )^{3}}}\right]_{z=\mathrm {i} }={\frac {\pi }{2}}}$$

On prend la dérivée première, dans les calculs précédents, car le pole est d'ordre 2. Ainsi, (z − i) est prise au carré, donc on utilise a dérivée première de f(z). Si on avait (z − i) élevé au cube, on aurait utilisé la dérivée seconde et divisé par 2!, etc. Le cas de (z − i) à la puissance 1 correspond à une dérivée d'ordre 0 — soit f(z) elle-même.

On doit montrer que l'intégrale sur le demi-cercle tend vers zéro pour a → ∞, par le lemme d'estimation

$${\displaystyle \left|\int _{\text{Arc}}f(z)\,\mathrm {d} z\right|\leq L({\text{Arc}})M}$$

avec M un majorant de |f(z)| sur l'arc et L désignant la longueur de l'arc. Ainsi,

$${\displaystyle \left|\int _{\text{Arc}}f(z)\,\mathrm {d} z\right|\leq {\frac {a\pi }{\left(a^{2}-1\right)^{2}}}\longrightarrow _{a\to \infty }0.}$$

Ainsi

$${\displaystyle \int _{-\infty }^{\infty }{\frac {1}{\left(x^{2}+1\right)^{2}}}\,\mathrm {d} x=\int _{-\infty }^{\infty }f(z)\,\mathrm {d} z=\lim _{a\to +\infty }\int _{-a}^{a}f(z)\,\mathrm {d} z={\frac {\pi }{2}}.\quad \square }$$

Par le théorème des résidus

On considère la série de Laurent de f(z) en i, qui est la seule singularité à considérer. On a

$${\displaystyle f(z)={\frac {-1}{4(z-\mathrm {i} )^{2}}}+{\frac {-\mathrm {i} }{4(z-\mathrm {i} )}}+{\frac {3}{16}}+{\frac {\mathrm {i} }{8}}(z-\mathrm {i} )+{\frac {-5}{64}}(z-\mathrm {i} )^{2}+\cdots }$$

Il est clair par l'observation que le résidu vaut −i/4, ainsi, la formule des résidus permet de conclure :

$${\displaystyle \oint _{C}f(z)\,\mathrm {d} z=\oint _{C}{\frac {1}{\left(z^{2}+1\right)^{2}}}\,\mathrm {d} z=2\pi \mathrm {i} \,\operatorname {Res} _{z=\mathrm {i} }f(z)=2\pi \mathrm {i} \left(-{\frac {\mathrm {i} }{4}}\right)={\frac {\pi }{2}}\quad \square }$$

Remarque sur le contour

On aurait pu choisir le demi-cercle dans la partie inférieure du plan complexe, qui entoure la singularité en −i. Pour avoir l'intégrale sur l'axe réel bien orienté, il faudrait parcourir le demi-cercle dans le sens horaire, ce qui change le signe de l'intégrale complète, mais pas le résultat final sur l'intégrale réelle.

L'intégrale

$${\displaystyle \int _{-\infty }^{\infty }{\frac {\mathrm {e} ^{\mathrm {i} tx}}{x^{2}+1}}\,\mathrm {d} x}$$

Le contour

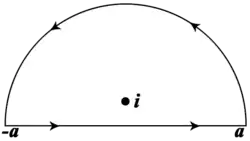
(qui apparait en théorie des probabilités comme un multiple scalaire de la fonction caractéristique de la loi de Cauchy) résiste aux techniques d'analyse élémentaire. On l'évalue en l'exprimant comme la limite d'intégrales de contour faites sur les demi-cercles dont le diamètre est formé par l'intervalle de la droite réelle entre −a et a et sur le demi-cercle centré en 0 et de rayon a, sur le demi-plan complexe des nombres de partie imaginaire positives, parcouru dans le sens anti-horaire. On prendra a plus grand que 1, de façon que l'affixe de i soit à l'intérieur de la courbe. L'intégrale de contour devient alors

$${\displaystyle \int _{C}{\frac {\mathrm {e} ^{\mathrm {i} tz}}{z^{2}+1}}\,\mathrm {d} z.}$$

Comme e^itz est une fonction entière (sans singularité sur le plan complexe), l'intégrande a des singularités aux lieux où le dénominateur z² + 1 s'annule. La factorisation donne z² + 1 = (z + i)(z − i), les singularités sont en z = i ou z = −i. Seul un de ces points est dans la zone délimitée par le contour. Le résidu de f(z) en z = i est

$${\displaystyle \lim _{z\to \mathrm {i} }(z-\mathrm {i} )f(z)=\lim _{z\to \mathrm {i} }(z-\mathrm {i} ){\frac {\mathrm {e} ^{\mathrm {i} tz}}{z^{2}+1}}=\lim _{z\to \mathrm {i} }(z-\mathrm {i} ){\frac {\mathrm {e} ^{\mathrm {i} tz}}{(z-\mathrm {i} )(z+\mathrm {i} )}}=\lim _{z\to \mathrm {i} }{\frac {\mathrm {e} ^{\mathrm {i} tz}}{z+\mathrm {i} }}={\frac {\mathrm {e} ^{-t}}{2\mathrm {i} }}.}$$

Selon le théorème des résidus, on a alors

$${\displaystyle \int _{C}f(z)\,\mathrm {d} z=2\pi \mathrm {i} \operatorname {Res} _{z=\mathrm {i} }f(z)=2\pi \mathrm {i} {\frac {\mathrm {e} ^{-t}}{2\mathrm {i} }}=\pi \mathrm {e} ^{-t}.}$$

Le contour C peut être séparé en une partie "droite" et un arc, donc

$${\displaystyle \int _{\text{droite}}+\int _{\text{arc}}=\pi \mathrm {e} ^{-t},}$$

est donc

$${\displaystyle \int _{-a}^{a}=\pi \mathrm {e} ^{-t}-\int _{\text{arc}}.}$$

Selon le lemme de Jordan, si t > 0 alors

$${\displaystyle \int _{\text{arc}}{\frac {\mathrm {e} ^{\mathrm {i} tz}}{z^{2}+1}}\,\mathrm {d} z\rightarrow 0{\mbox{ pour }}a\rightarrow \infty .}$$

Ainsi, si t > 0 alors

$${\displaystyle \int _{-\infty }^{\infty }{\frac {\mathrm {e} ^{\mathrm {i} tx}}{x^{2}+1}}\,\mathrm {d} x=\pi \mathrm {e} ^{-t}.}$$

Un argument similaire avec un arc qui tourne autour de −i au lieu de i montre que si t < 0 alors

$${\displaystyle \int _{-\infty }^{\infty }{\frac {\mathrm {e} ^{\mathrm {i} tx}}{x^{2}+1}}\,\mathrm {d} x=\pi \mathrm {e} ^{t},}$$

ainsi, on obtient:

$${\displaystyle \int _{-\infty }^{\infty }{\frac {\mathrm {e} ^{\mathrm {i} tx}}{x^{2}+1}}\,\mathrm {d} x=\pi \mathrm {e} ^{-|t|}.\quad \square }$$

(Si t = 0 alors l'intégrale peut être calculée grâce à l'analyse réelle et vaut π.)

Certaines substitutions peuvent être aux intégrales impliquant des fonctions trigonométriques, ainsi l'intégrande est transformé en une fonction rationnelle d'une variable complexe et on peut appliquer les méthodes vues au-dessus pour calculer l'intégrale. On peut considérer par exemple

$${\displaystyle \int _{-\pi }^{\pi }{\frac {1}{1+3(\cos t)^{2}}}\,\mathrm {d} t.}$$

On veut faire une substitution de z = e^it. On applique la formule d'Euler

$${\displaystyle \cos t={\frac {1}{2}}\left(\mathrm {e} ^{\mathrm {i} t}+\mathrm {e} ^{-\mathrm {i} t}\right)={\frac {1}{2}}\left(z+{\frac {1}{z}}\right)}$$

et donc

$${\displaystyle {\frac {\mathrm {d} z}{\mathrm {d} t}}=\mathrm {i} z,\ \mathrm {d} t={\frac {\mathrm {d} z}{\mathrm {i} z}}.}$$

On considère C le cercle unité, ce qui donne par substitution :

$${\displaystyle {\begin{aligned}\oint _{C}{\frac {1}{1+3\left({\frac {1}{2}}\left(z+{\frac {1}{z}}\right)\right)^{2}}}\,{\frac {\mathrm {d} z}{\mathrm {i} z}}&=\oint _{C}{\frac {1}{1+{\frac {3}{4}}\left(z+{\frac {1}{z}}\right)^{2}}}{\frac {1}{\mathrm {i} z}}\,\mathrm {d} z\\&=\oint _{C}{\frac {-\mathrm {i} }{z+{\frac {3}{4}}z\left(z+{\frac {1}{z}}\right)^{2}}}\,\mathrm {d} z\\&=-\mathrm {i} \oint _{C}{\frac {\mathrm {d} z}{z+{\frac {3}{4}}z\left(z^{2}+2+{\frac {1}{z^{2}}}\right)}}\\&=-\mathrm {i} \oint _{C}{\frac {\mathrm {d} z}{z+{\frac {3}{4}}\left(z^{3}+2z+{\frac {1}{z}}\right)}}\\&=-\mathrm {i} \oint _{C}{\frac {\mathrm {d} z}{{\frac {3}{4}}z^{3}+{\frac {5}{2}}z+{\frac {3}{4z}}}}\\&=-\mathrm {i} \oint _{C}{\frac {4}{3z^{3}+10z+{\frac {3}{z}}}}\,\mathrm {d} z\\&=-4\mathrm {i} \oint _{C}{\frac {\mathrm {d} z}{3z^{3}+10z+{\frac {3}{z}}}}\\&=-4\mathrm {i} \oint _{C}{\frac {z}{3z^{4}+10z^{2}+3}}\,\mathrm {d} z\\&=-4\mathrm {i} \oint _{C}{\frac {z}{3\left(z+\mathrm {i} {\sqrt {3}}\right)\left(z-\mathrm {i} {\sqrt {3}}\right)\left(z+{\frac {\mathrm {i} }{\sqrt {3}}}\right)\left(z-{\frac {\mathrm {i} }{\sqrt {3}}}\right)}}\,\mathrm {d} z\\&=-{\frac {4\mathrm {i} }{3}}\oint _{C}{\frac {z}{\left(z+\mathrm {i} {\sqrt {3}}\right)\left(z-\mathrm {i} {\sqrt {3}}\right)\left(z+{\frac {\mathrm {i} }{\sqrt {3}}}\right)\left(z-{\frac {\mathrm {i} }{\sqrt {3}}}\right)}}\,\mathrm {d} z.\end{aligned}}}$$

Les singularités à considérer sont en ${\displaystyle {\tfrac {\pm \mathrm {i} }{\sqrt {3}}}.}$ Soit C₁ un petit cercle autour de ${\displaystyle {\tfrac {\mathrm {i} }{\sqrt {3}}},}$ et C₂ un petit cercle autour de ${\displaystyle {\tfrac {-\mathrm {i} }{\sqrt {3}}}.}$ On en déduit :

$${\displaystyle {\begin{aligned}&-{\frac {4\mathrm {i} }{3}}\left[\oint _{C_{1}}{\frac {\frac {z}{\left(z+\mathrm {i} {\sqrt {3}}\right)\left(z-\mathrm {i} {\sqrt {3}}\right)\left(z+{\frac {\mathrm {i} }{\sqrt {3}}}\right)}}{z-{\frac {\mathrm {i} }{\sqrt {3}}}}}\,\mathrm {d} z+\oint _{C_{2}}{\frac {\frac {z}{\left(z+\mathrm {i} {\sqrt {3}}\right)\left(z-\mathrm {i} {\sqrt {3}}\right)\left(z-{\frac {\mathrm {i} }{\sqrt {3}}}\right)}}{z+{\frac {\mathrm {i} }{\sqrt {3}}}}}\,\mathrm {d} z\right]\\={}&-{\frac {4\mathrm {i} }{3}}\left[2\pi \mathrm {i} \left[{\frac {z}{\left(z+\mathrm {i} {\sqrt {3}}\right)\left(z-\mathrm {i} {\sqrt {3}}\right)\left(z+{\frac {\mathrm {i} }{\sqrt {3}}}\right)}}\right]_{z={\frac {\mathrm {i} }{\sqrt {3}}}}+2\pi \mathrm {i} \left[{\frac {z}{\left(z+\mathrm {i} {\sqrt {3}}\right)\left(z-\mathrm {i} {\sqrt {3}}\right)\left(z-{\frac {\mathrm {i} }{\sqrt {3}}}\right)}}\right]_{z=-{\frac {\mathrm {i} }{\sqrt {3}}}}\right]\\={}&{\frac {8\pi }{3}}\left[{\frac {\frac {\mathrm {i} }{\sqrt {3}}}{\left({\frac {\mathrm {i} }{\sqrt {3}}}+\mathrm {i} {\sqrt {3}}\right)\left({\frac {\mathrm {i} }{\sqrt {3}}}-\mathrm {i} {\sqrt {3}}\right)\left({\frac {\mathrm {i} }{\sqrt {3}}}+{\frac {\mathrm {i} }{\sqrt {3}}}\right)}}+{\frac {-{\frac {\mathrm {i} }{\sqrt {3}}}}{\left(-{\frac {\mathrm {i} }{\sqrt {3}}}+\mathrm {i} {\sqrt {3}}\right)\left(-{\frac {\mathrm {i} }{\sqrt {3}}}-\mathrm {i} {\sqrt {3}}\right)\left(-{\frac {\mathrm {i} }{\sqrt {3}}}-{\frac {\mathrm {i} }{\sqrt {3}}}\right)}}\right]\\={}&{\frac {8\pi }{3}}\left[{\frac {\frac {\mathrm {i} }{\sqrt {3}}}{\left({\frac {4}{\sqrt {3}}}\mathrm {i} \right)\left(-{\frac {2}{\mathrm {i} {\sqrt {3}}}}\right)\left({\frac {2}{\mathrm {i} {\sqrt {3}}}}\right)}}+{\frac {-{\frac {\mathrm {i} }{\sqrt {3}}}}{\left({\frac {2}{\sqrt {3}}}\mathrm {i} \right)\left(-{\frac {4}{\sqrt {3}}}\mathrm {i} \right)\left(-{\frac {2}{\sqrt {3}}}\mathrm {i} \right)}}\right]\\={}&{\frac {8\pi }{3}}\left[{\frac {\frac {\mathrm {i} }{\sqrt {3}}}{\mathrm {i} \left({\frac {4}{\sqrt {3}}}\right)\left({\frac {2}{\sqrt {3}}}\right)\left({\frac {2}{\sqrt {3}}}\right)}}+{\frac {-{\frac {\mathrm {i} }{\sqrt {3}}}}{-\mathrm {i} \left({\frac {2}{\sqrt {3}}}\right)\left({\frac {4}{\sqrt {3}}}\right)\left({\frac {2}{\sqrt {3}}}\right)}}\right]\\={}&{\frac {8\pi }{3}}\left[{\frac {\frac {1}{\sqrt {3}}}{\left({\frac {4}{\sqrt {3}}}\right)\left({\frac {2}{\sqrt {3}}}\right)\left({\frac {2}{\sqrt {3}}}\right)}}+{\frac {\frac {1}{\sqrt {3}}}{\left({\frac {2}{\sqrt {3}}}\right)\left({\frac {4}{\sqrt {3}}}\right)\left({\frac {2}{\sqrt {3}}}\right)}}\right]\\={}&{\frac {8\pi }{3}}\left[{\frac {\frac {1}{\sqrt {3}}}{\frac {16}{3{\sqrt {3}}}}}+{\frac {\frac {1}{\sqrt {3}}}{\frac {16}{3{\sqrt {3}}}}}\right]\\={}&{\frac {8\pi }{3}}\left[{\frac {3}{16}}+{\frac {3}{16}}\right]\\={}&\pi .\end{aligned}}}$$

La méthode décrite ici est utile pour les intégrales de la forme

$${\displaystyle \int _{0}^{2\pi }{\frac {P\left(\sin(t),\sin(2t),\ldots ,\cos(t),\cos(2t),\ldots \right)}{Q\left(\sin(t),\sin(2t),\ldots ,\cos(t),\cos(2t),\ldots \right)}}\,\mathrm {d} t}$$

où P et Q sont des polynômes, i.e. une fonction rationnelle de termes trigonométrique est intégrée. On notera que les bornes d'intégration peuvent être π est -π, comme dans l'exemple, ou les extrémités tout intervalle de longueur 2π.

L'astuce est d'utiliser la substitution z = e^it où dz = ie^it dt et donc

$${\displaystyle {\frac {1}{\mathrm {i} z}}\,\mathrm {d} z=\mathrm {d} t.}$$

Cette substitution envoie l'intervalle [0, 2π] sur le cercle unité. De plus,

$${\displaystyle \sin(kt)={\frac {\mathrm {e} ^{\mathrm {i} kt}-\mathrm {e} ^{-\mathrm {i} kt}}{2\mathrm {i} }}={\frac {z^{k}-z^{-k}}{2i}}}$$

et

$${\displaystyle \cos(kt)={\frac {\mathrm {e} ^{\mathrm {i} kt}+\mathrm {e} ^{-\mathrm {i} kt}}{2}}={\frac {z^{k}+z^{-k}}{2}}}$$

de sorte qu'une fonction rational f(z) en z résulte de la substitution, est l'intégrale devient

$${\displaystyle \oint _{|z|=1}f(z){\frac {1}{\mathrm {i} z}}\,\mathrm {d} z}$$

qui à son tour se calcule en sommant les résidus de f(z)1/iz dans le cercle unité.

On prend par exemple l'intégrale

$${\displaystyle I=\int _{0}^{\frac {\pi }{2}}{\frac {1}{1+(\sin t)^{2}}}\,\mathrm {d} t.}$$

On doit d'abord voir que

$${\displaystyle I={\frac {1}{4}}\int _{0}^{2\pi }{\frac {1}{1+(\sin t)^{2}}}\,\mathrm {d} t.}$$

La substitution donne

$${\displaystyle {\frac {1}{4}}\oint _{|z|=1}{\frac {4\mathrm {i} z}{z^{4}-6z^{2}+1}}\,\mathrm {d} z=\oint _{|z|=1}{\frac {\mathrm {i} z}{z^{4}-6z^{2}+1}}\,\mathrm {d} z.}$$

Les poles de cette fonction sont en 1 ± √2 et −1 ± √2. De ces quatre poles, 1 + √2 et −1 − √2 sont hors du cercle unité (en rouge), mais 1 − √2 et −1 + √2 (en bleu) sont à l'intérieur. Les résidus correspondants sont tous deux égaux à −i√2/16, ainsi l'intégrale vaut

$${\displaystyle I=2\pi \mathrm {i} \times 2\times \left(-{\frac {\sqrt {2}}{16}}\mathrm {i} \right)=\pi {\frac {\sqrt {2}}{4}}.}$$

On considère l'intégrale réelle

$${\displaystyle \int _{0}^{\infty }{\frac {\sqrt {x}}{x^{2}+6x+8}}\,\mathrm {d} x.}$$

On peut d'abord commencer par poser l'intégrale de contour

$${\displaystyle \int _{C}{\frac {\sqrt {z}}{z^{2}+6z+8}}\,\mathrm {d} z=I.}$$

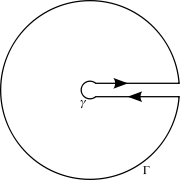
Si les résultats utilisés pour le calcul des résidus restent les mêmes, il faut noter que z^1/2 = e^{(Log z)/2}, donc z^1/2 a un point de branchement, ce qui doit être pris en compte dans le choix du contour C. Normalement le branchement du logarithme est définie comme le demi-axe réel négatif, cependant, ce choix rend le calcul de l'intégrale un peu compliqué, donc on choisira le demi-axe réel positif.

On utilise alors le contour du "trou de serrure", formé d'un petit cercle ouvert de rayon ε, s'étendant sur un segment parallèle au demi-axe jusqu'à un autre cercle ouvert.

Notons que z = −2 et z = −4 sont dans le grand cercle. Ce sont les deux poles restants, dérivables en factorisant le dénominateur de l'intégrande. Le point de branchement en z = 0 est évité en le contournant.

Soit γ le petit cercle de rayon ε, Γ le plus grand, de rayon R, alors

$${\displaystyle \int _{C}=\int _{\varepsilon }^{R}+\int _{\Gamma }+\int _{R}^{\varepsilon }+\int _{\gamma }.}$$

On peut voir que les intégrales sur Γ et γ tendent toutes deux vers 0 pour ε → 0 et R → ∞, par une estimation donnée au-dessus, ce qui laisse deux termes. Comme z^1/2 = e^{(Log z)/2}, sur le contour hors du branchement, on a gagné 2π en argument le long de γ. (Par l'identité d'Euler, e^iπ représente le vecteur unité, donc a un log égal à π, ce qui correspond à l'argument de z. Le coefficient de 1/2 force à utiliser 2π.) Ainsi

$${\displaystyle {\begin{aligned}\int _{R}^{\varepsilon }{\frac {\sqrt {z}}{z^{2}+6z+8}}\,\mathrm {d} z&=\int _{R}^{\varepsilon }{\frac {\mathrm {e} ^{{\frac {1}{2}}\operatorname {Log} z}}{z^{2}+6z+8}}\,\mathrm {d} z\\[6pt]&=\int _{R}^{\varepsilon }{\frac {\mathrm {e} ^{{\frac {1}{2}}(\log |z|+\mathrm {i} \arg {z})}}{z^{2}+6z+8}}\,\mathrm {d} z\\[6pt]&=\int _{R}^{\varepsilon }{\frac {\mathrm {e} ^{{\frac {1}{2}}\log |z|}e^{{\frac {1}{2}}(2\pi \mathrm {i} )}}{z^{2}+6z+8}}\,\mathrm {d} z\\[6pt]&=\int _{R}^{\varepsilon }{\frac {\mathrm {e} ^{{\frac {1}{2}}\log |z|}e^{\pi \mathrm {i} }}{z^{2}+6z+8}}\,\mathrm {d} z\\[6pt]&=\int _{R}^{\varepsilon }{\frac {-{\sqrt {z}}}{z^{2}+6z+8}}\,\mathrm {d} z\\[6pt]&=\int _{\varepsilon }^{R}{\frac {\sqrt {z}}{z^{2}+6z+8}}\,\mathrm {d} z.\end{aligned}}}$$

Ainsi :

$${\displaystyle \int _{C}{\frac {\sqrt {z}}{z^{2}+6z+8}}\,\mathrm {d} z=2\int _{0}^{\infty }{\frac {\sqrt {x}}{x^{2}+6x+8}}\,\mathrm {d} x.}$$

Avec le théorème des résidus ou la formule intégrale de Cauchy (d'abord en la méthode des fractions partielles pour dériver une somme de deux intégrales de contour simples) on obtient

$${\displaystyle \pi \mathrm {i} \left({\frac {\mathrm {i} }{\sqrt {2}}}-\mathrm {i} \right)=\int _{0}^{\infty }{\frac {\sqrt {x}}{x^{2}+6x+8}}\,\mathrm {d} x=\pi \left(1-{\frac {1}{\sqrt {2}}}\right).\quad \square }$$

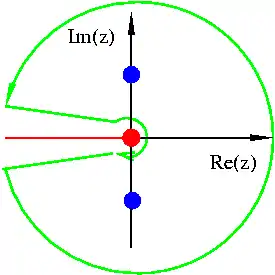
Cette section traite des intégrales semblables à l'exemple suivant :

$${\displaystyle \int _{0}^{\infty }{\frac {\log x}{\left(1+x^{2}\right)^{2}}}\,\mathrm {d} x.}$$

Pour le calcul des intégrales, on utilise la fonction

$${\displaystyle f(z)=\left({\frac {\log z}{1+z^{2}}}\right)^{2}}$$

et la branche du logarithme correspond à −π < arg(z) ≤ π.

On va calculer l'intégrale de f(z) le long du contour "trou de serrure" décrit en image. Comme il s'avère que cette intégrale est un multiple de l'intégrale initiale et par le théorème des résidus, on a

$${\displaystyle {\begin{aligned}\left(\int _{R}+\int _{M}+\int _{N}+\int _{r}\right)f(z)\,\mathrm {d} z&=2\pi \mathrm {i} \left(\operatorname {Res} _{z=i}f(z)+\operatorname {Res} _{z=-i}f(z)\right)\\&=2\pi \mathrm {i} \left(-{\frac {\pi }{4}}+{\frac {1}{16}}\mathrm {i} \pi ^{2}-{\frac {\pi }{4}}-{\frac {1}{16}}\mathrm {i} \pi ^{2}\right)\\&=-\mathrm {i} \pi ^{2}.\end{aligned}}}$$

Soit R le rayon du grand cercle, et r le rayon du petit. On note le segment supérieur M, et N le segment inférieur. Comme auparavant, on prend la limite en R → ∞ et r → 0. Les contributions sur les deux cercles tendent à s'annuler. Par exemple, on peut majorer, par le lemme d'estimation avec :

$${\displaystyle \left|\int _{R}f(z)\,\mathrm {d} z\right|\leq 2\pi R{\frac {(\log R)^{2}+\pi ^{2}}{\left(R^{2}-1\right)^{2}}}\to 0.}$$

Afin de calculer les contributions de M et N on pose z = −x + iε sur M et z = −x − iε sur N, avec 0 < x < +∞:

$${\displaystyle {\begin{aligned}-\mathrm {i} \pi ^{2}&=\left(\int _{R}+\int _{M}+\int _{N}+\int _{r}\right)f(z)\,\mathrm {d} z\\[6pt]&=\left(\int _{M}+\int _{N}\right)f(z)\,\mathrm {d} z&&\int _{R},\int _{r}\rightarrow 0\\[6pt]&=-\int _{\infty }^{0}\left({\frac {\log(-x+\mathrm {i} \varepsilon )}{1+(-x+\mathrm {i} \varepsilon )^{2}}}\right)^{2}\,\mathrm {d} x-\int _{0}^{\infty }\left({\frac {\log(-x-\mathrm {i} \varepsilon )}{1+(-x-i\varepsilon )^{2}}}\right)^{2}\,\mathrm {d} x\\[6pt]&=\int _{0}^{\infty }\left({\frac {\log(-x+\mathrm {i} \varepsilon )}{1+(-x+\mathrm {i} \varepsilon )^{2}}}\right)^{2}\,\mathrm {d} x-\int _{0}^{\infty }\left({\frac {\log(-x-\mathrm {i} \varepsilon )}{1+(-x-i\varepsilon )^{2}}}\right)^{2}\,\mathrm {d} x\\[6pt]&=\int _{0}^{\infty }\left({\frac {\log x+\mathrm {i} \pi }{1+x^{2}}}\right)^{2}\,\mathrm {d} x-\int _{0}^{\infty }\left({\frac {\log x-\mathrm {i} \pi }{1+x^{2}}}\right)^{2}\,\mathrm {d} x&&\varepsilon \to 0\\&=\int _{0}^{\infty }{\frac {(\log x+\mathrm {i} \pi )^{2}-(\log x-\mathrm {i} \pi )^{2}}{\left(1+x^{2}\right)^{2}}}\,\mathrm {d} x\\[6pt]&=\int _{0}^{\infty }{\frac {4\pi \mathrm {i} \log x}{\left(1+x^{2}\right)^{2}}}\,\mathrm {d} x\\[6pt]&=4\pi \mathrm {i} \int _{0}^{\infty }{\frac {\log x}{\left(1+x^{2}\right)^{2}}}\,\mathrm {d} x\end{aligned}}}$$

ce qui donne

$${\displaystyle \int _{0}^{\infty }{\frac {\log x}{\left(1+x^{2}\right)^{2}}}\,\mathrm {d} x=-{\frac {\pi }{4}}.}$$

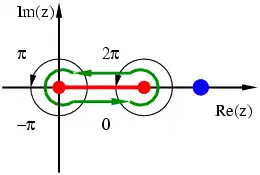
On veut évaluer

$${\displaystyle I=\int _{0}^{3}{\frac {x^{\frac {3}{4}}(3-x)^{\frac {1}{4}}}{5-x}}\,\mathrm {d} x.}$$

ce qui implique de considérer

$${\displaystyle f(z)=z^{\frac {3}{4}}(3-z)^{\frac {1}{4}}.}$$

On construit f(z) telle qu'il y ait un branchement sur [0, 3], en rouge dans le schéma. Pour ce faire, on choisit deux branchements du logarithme, ce qui donne

$${\displaystyle z^{\frac {3}{4}}=\exp \left({\frac {3}{4}}\log z\right)\quad {\mbox{avec}}\quad -\pi \leq \arg z<\pi }$$

et

$${\displaystyle (3-z)^{\frac {1}{4}}=\exp \left({\frac {1}{4}}\log(3-z)\right)\quad {\mbox{avec}}\quad 0\leq \arg(3-z)<2\pi .}$$

Le branchement de z^3/4 est donc ]−∞, 0] et le branchement de (3 − z)^1/4 est ]−∞, 3]. Il est simple de voir que le branchement du produit des deux, i.e. f(z), est [0, 3], car f(z) est en fait continue sur ]−∞, 0[. Ceci apparait pour z = −r < 0 et quand on approche le branchement par au-dessus, f(z) a la valeur

$${\displaystyle r^{\frac {3}{4}}\mathrm {e} ^{{\frac {3}{4}}\mathrm {i} \pi }(3+r)^{\frac {1}{4}}\mathrm {e} ^{{\frac {2}{4}}\mathrm {i} \pi }=r^{\frac {3}{4}}(3+r)^{\frac {1}{4}}\mathrm {e} ^{{\frac {5}{4}}\mathrm {i} \pi }.}$$

En l'approchant par en-dessous, f(z) a la valeur

$${\displaystyle r^{\frac {3}{4}}\mathrm {e} ^{-{\frac {3}{4}}\mathrm {i} \pi }(3+r)^{\frac {1}{4}}\mathrm {e} ^{{\frac {0}{4}}\mathrm {i} \pi }=r^{\frac {3}{4}}(3+r)^{\frac {1}{4}}\mathrm {e} ^{-{\frac {3}{4}}\mathrm {i} \pi }.}$$

Mais

$${\displaystyle \mathrm {e} ^{-{\frac {3}{4}}\mathrm {i} \pi }=\mathrm {e} ^{{\frac {5}{4}}\mathrm {i} \pi },}$$

donc il y a continuité à travers le branchement. C'est illustré dans le schéma, où les deux cercles noirs orientés sont notés avec la valeur correspondante de l'argument du logarithme dans z^3/4 et (3 − z)^1/4.

On utilise le contour en vert dans le schéma. Pour faire cela, on doit calculer la valeur de f(z) le long des segments juste au-dessus et en-dessous du branchement.

Soit z = r (à la limite, i.e. quand les deux cercles verts se réduisent vers un point), où 0 ≤ r ≤ 3. Le long du segment d'au-dessus, on trouve que f(z) a la valeur

$${\displaystyle r^{\frac {3}{4}}\mathrm {e} ^{{\frac {0}{4}}\mathrm {i} \pi }(3-r)^{\frac {1}{4}}\mathrm {e} ^{{\frac {2}{4}}\mathrm {i} \pi }=\mathrm {i} r^{\frac {3}{4}}(3-r)^{\frac {1}{4}}}$$

et le long du segment d'en-dessous,

$${\displaystyle r^{\frac {3}{4}}\mathrm {e} ^{{\frac {0}{4}}\mathrm {i} \pi }(3-r)^{\frac {1}{4}}\mathrm {e} ^{{\frac {0}{4}}\mathrm {i} \pi }=r^{\frac {3}{4}}(3-r)^{\frac {1}{4}}.}$$

Il suit que l'intégrale de f(z)/5 − z le long du segment vaut −iI à la limite, et le long du segment d'en-dessous, I.

Si on peut montrer que les intégrale sur les deux cercles s'annulent à la limite, alors on a également la valeur de I, par le théorème des résidus. On note ρ le rayon des cercles verts, avec ρ < 0,001 et ρ → 0, pour appliquer le lemme d'estimation. Pour le cercle de gauche C_L on obtient

$${\displaystyle \left|\int _{C_{\mathrm {L} }}{\frac {f(z)}{5-z}}\mathrm {d} z\right|\leq 2\pi \rho {\frac {\rho ^{\frac {3}{4}}3.001^{\frac {1}{4}}}{4.999}}\in {\mathcal {O}}\left(\rho ^{\frac {7}{4}}\right)\to 0.}$$

De même, sur le cercle à droite C_R, on a

$${\displaystyle \left|\int _{C_{\mathrm {R} }}{\frac {f(z)}{5-z}}\mathrm {d} z\right|\leq 2\pi \rho {\frac {3.001^{\frac {3}{4}}\rho ^{\frac {1}{4}}}{1.999}}\in {\mathcal {O}}\left(\rho ^{\frac {5}{4}}\right)\to 0.}$$

Avec le théorème des résidus, on a

$${\displaystyle (-\mathrm {i} +1)I=-2\mathrm {i} \pi \left(\operatorname {Res} _{z=5}{\frac {f(z)}{5-z}}+\operatorname {Res} _{z=\infty }{\frac {f(z)}{5-z}}\right).}$$

où le signe moins vient que le chemin autour des résidus est parcouru dans le sens horaire. En utilisant la branche du logarithme défini plus tôt, on trouve

$${\displaystyle \operatorname {Res} _{z=5}{\frac {f(z)}{5-z}}=-5^{\frac {3}{4}}\mathrm {e} ^{{\frac {1}{4}}\log(-2)}.}$$

Le pole est montré en bleu sur le schéma. La valeur se simplifie en

$${\displaystyle -5^{\frac {3}{4}}\mathrm {e} ^{{\frac {1}{4}}(\log 2+\mathrm {i} \pi )}=-\mathrm {e} ^{{\frac {1}{4}}\mathrm {i} \pi }5^{\frac {3}{4}}2^{\frac {1}{4}}.}$$

On utilise la formule suivante pour les résidus à l'infini :

$${\displaystyle \operatorname {Res} _{z=\infty }h(z)=\operatorname {Res} _{z=0}\left(-{\frac {1}{z^{2}}}h\left({\frac {1}{z}}\right)\right).}$$

Par substitution, on trouve

$${\displaystyle {\frac {1}{5-{\frac {1}{z}}}}=-z\left(1+5z+5^{2}z^{2}+5^{3}z^{3}+\cdots \right)}$$

et

$${\displaystyle \left({\frac {1}{z^{3}}}\left(3-{\frac {1}{z}}\right)\right)^{\frac {1}{4}}={\frac {1}{z}}(3z-1)^{\frac {1}{4}}={\frac {1}{z}}\mathrm {e} ^{{\frac {1}{4}}\mathrm {i} \pi }(1-3z)^{\frac {1}{4}},}$$

en utilisant l'égalité −1 = e^iπ sur la deuxième branche du logarithme. Ensuite, on applique le développement binomial, qui donne

$${\displaystyle {\frac {1}{z}}\mathrm {e} ^{{\frac {1}{4}}\mathrm {i} \pi }\left(1-{1/4 \choose 1}3z+{1/4 \choose 2}3^{2}z^{2}-{1/4 \choose 3}3^{3}z^{3}+\cdots \right).}$$

On en conclut

$${\displaystyle \operatorname {Res} _{z=\infty }{\frac {f(z)}{5-z}}=\mathrm {e} ^{{\frac {1}{4}}\mathrm {i} \pi }\left(5-{\frac {3}{4}}\right)=\mathrm {e} ^{{\frac {1}{4}}\mathrm {i} \pi }{\frac {17}{4}}.}$$

Enfin, il suit que la valeur de I est de

$${\displaystyle I=2\pi \mathrm {i} {\frac {\mathrm {e} ^{{\frac {1}{4}}\mathrm {i} \pi }}{-1+\mathrm {i} }}\left({\frac {17}{4}}-5^{\frac {3}{4}}2^{\frac {1}{4}}\right)=2\pi 2^{-{\frac {1}{2}}}\left({\frac {17}{4}}-5^{\frac {3}{4}}2^{\frac {1}{4}}\right)}$$

dont on tire

$${\displaystyle I={\frac {\pi }{2{\sqrt {2}}}}\left(17-5^{\frac {3}{4}}2^{\frac {9}{4}}\right)={\frac {\pi }{2{\sqrt {2}}}}\left(17-40^{\frac {3}{4}}\right).}$$

Soit le champ de vecteurs F = sin(2x) + sin(2y) + sin(2z), dans le pavé

$${\displaystyle {0\leq x\leq 1}\ ,\ {0\leq y\leq 3}\ ,\ {-1\leq z\leq 4}}$$

L'intégrale de contour double correspondante sera définie comme:

$${\displaystyle \int \!\!\!\!\!\!\!\subset \!\!\!\supset \!\!\!\!\!\!\!\int _{S}\mathbf {F} \cdot \mathbf {n} \,\mathrm {d} S}$$

On évalue maintenant ∇ • F, par l'intégrale triple correspondante :

$${\displaystyle {\begin{aligned}\int \!\!\!\!\!\!\!\subset \!\!\!\supset \!\!\!\!\!\!\!\int _{S}\mathbf {F} \cdot \mathbf {n} \,\mathrm {d} S&=\int \!\!\!\!\!\int \!\!\!\!\!\int _{V}\left({\frac {\partial F_{x}}{\partial x}}+{\frac {\partial F_{y}}{\partial y}}+{\frac {\partial F_{z}}{\partial z}}\right)\,\mathrm {d} V\\[6pt]&=\int \!\!\!\!\!\int \!\!\!\!\!\int _{V}\left({\frac {\partial \sin(2x)}{\partial x}}+{\frac {\partial \sin(2y)}{\partial y}}+{\frac {\partial \sin(2z)}{\partial z}}\right)\,\mathrm {d} V\\[6pt]&=\int \!\!\!\!\!\int \!\!\!\!\!\int _{V}2\left(\cos(2x)+\cos(2y)+\cos(2z)\right)\,\mathrm {d} V\\[6pt]&=\int _{0}^{1}\int _{0}^{3}\int _{-1}^{4}2(\cos(2x)+\cos(2y)+\cos(2z))\,\mathrm {d} x\,\mathrm {d} y\,\mathrm {d} z\\[6pt]&=\int _{0}^{1}\int _{0}^{3}(10\cos(2y)+\sin(8)+\sin(2)+10\cos(z))\,\mathrm {d} y\,\mathrm {d} z\\[6pt]&=\int _{0}^{1}(30\cos(2z)+3\sin(2)+3\sin(8)+5\sin(6))\,\mathrm {d} z\\[6pt]&=18\sin(2)+3\sin(8)+5\sin(6)\end{aligned}}}$$

On considère le champ de vecteurs F = u⁴ + x⁵ + y⁶ + z^-3, et n désigne la quatrième dimension. On borne ce champ de vecteurs par le pavé :

$${\displaystyle {0\leq x\leq 1}\ ,\ {-10\leq y\leq 2\pi }\ ,\ {4\leq z\leq 5}\ ,\ {-1\leq u\leq 3}}$$

On utilise donc le théorème de la divergence. Un élément de volume est donc dV = dx dy dz du.