Loi z de Fisher

En théorie des probabilités et en statistique, la loi z de Fisher est construite à partir de la loi de Fisher en prenant la moitié de son logarithme :

Z={\frac {1}{2}}\log X

où X suit une loi de Fisher.

Loi z de Fisher
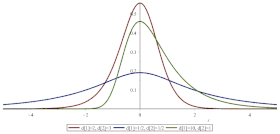Densité de probabilité



Paramètres	$d_{1}>0,\,d_{2}>0$ , (degrés de liberté)
Support	${\displaystyle x\in ]-\infty$
Densité de probabilité	${\textstyle {\frac {2d_{1}^{d_{1}/2}d_{2}^{d_{2}/2}}{\mathrm {B} (d_{1}/2,d_{2}/2)}}{\frac {{\rm {e}}^{d_{1}z}}{\left(d_{1}{\rm {e}}^{2z}+d_{2}\right)^{\left(d_{1}+d_{2}\right)/2}}}\!}$
Mode	0
Fonction caractéristique	${\textstyle \exp \!\left[\;{\rm {i}}t\mu -\|c\,t\|(1+{\tfrac {2{\rm {i}}}{\pi }}\log(\|t\|)\right]}$

Ronald Fisher

Elle est initialement apparue dans un travail[1] de Ronald Fisher lors du congrès international des mathématiciens de 1924 à Toronto, et intitulé On a distribution yielding the error functions of several well-known statistics que l'on peut traduire par : Sur une loi modélisant les fonctions d'erreur de plusieurs statistiques bien connues.

Définition

La densité de probabilité et la fonction de répartition peuvent être obtenues grâce à celles de la loi de Fisher par l'application $x\mapsto {\rm {e}}^{2x}$ . Cependant la moyenne et la variance ne sont pas les images de cette application. La densité est donnée par[2] - [3] :

f(x;d_{1},d_{2})={\frac {2d_{1}^{d_{1}/2}d_{2}^{d_{2}/2}}{\mathrm {B} (d_{1}/2,d_{2}/2)}}{\frac {{\rm {e}}^{d_{1}x}}{\left(d_{1}{\rm {e}}^{2x}+d_{2}\right)^{(d_{1}+d_{2})/2}}},

où $B$ est la fonction bêta.

Lien avec d'autres lois

Si $X\sim \operatorname {FisherZ} (n,m)$ alors $e^{2X}\sim \operatorname {F} (n,m)\,$ (loi de Fisher)
Si $X\sim \operatorname {F} (n,m)$ alors ${\tfrac {\log {X}}{2}}\sim \operatorname {FisherZ} (n,m)$
Lorsque le nombre de degré de liberté est grand ( $n_{1},n_{2}\rightarrow \infty$ ), la loi approche la loi normale de moyenne[2] ${\bar {X}}=(1/d_{2}-1/d_{1})/2$ et de variance $\sigma _{X}^{2}=(1/d_{1}+1/d_{2})/2.$

Références

(en) R.A. Fisher, « On a Distribution Yielding the Error Functions of Several Well Known Statistics », Proceedings of the International Congress of Mathematics, Toronto, vol. 2,‎ 1924, p. 805-813 (lire en ligne)

Proceedings of the International Congress of Mathematics, Toronto, 2: 805-813 (1924)
Leo A. Aroian, « A study of R. A. Fisher's z distribution and the related F distribution », The Annals of Mathematical Statistics, vol. 12, n^o 4,‎ décembre 1941 (JSTOR 2235955)
Charles Ernest Weatherburn, A first course in mathematical statistics

Liens externes

(en) Eric W. Weisstein, « Fishers' z Distribution », sur MathWorld

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.