Loi hyper-exponentielle

En théorie des probabilités et en statistique, la loi hyper-exponentielle (ou loi hyper-exponentielle-n) est une loi de probabilité continue mélangeant plusieurs lois exponentielles. Elle dépend de trois paramètres : n le nombre de lois exponentielles indépendantes, $(\lambda _{i},1\leq i\leq n)$ les paramètres de ces lois exponentielles et $(p_{i},1\leq i\leq n)$ une pondération de ces lois. Le terme hyper vient du fait que le coefficient de variation de la loi est supérieur à 1, comparativement à la loi hypo-exponentielle dont le coefficient de variation est inférieur à 1 et à la loi exponentielle dont le coefficient vaut 1.

Loi hyper-exponentielle
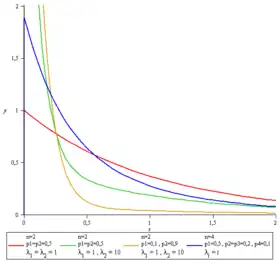Densité de probabilité


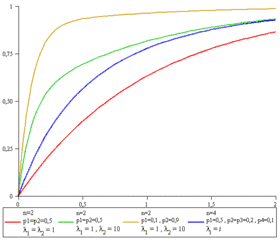Fonction de répartition

Paramètres	n=1,2,... $0<p_{i}\leq 1$ paramètres de mélange $\lambda _{i}>0$
Support	$x\in [0;+\infty [\,$
Densité de probabilité	$\sum _{i=1}^{n}p_{i}\lambda _{i}e^{-\lambda _{i}y}$
Fonction de répartition	$1-\sum _{i=1}^{n}p_{i}e^{-\lambda _{i}y}$
Espérance	$\sum _{i=1}^{n}{\frac {p_{i}}{\lambda _{i}}}$
Fonction caractéristique	$\displaystyle \prod _{i=1}^{N}{\frac {\lambda _{i}p_{i}}{\lambda _{i}+\xi }}$

C'est une loi utilisée dans la théorie des files d'attente[1] dans le cas d'une simulation de n serveurs en parallèle.

Définition

La loi hyper-exponentielle est, en un certain sens, un mélange de plusieurs lois exponentielles. Notons $(X_{i},1\leq i\leq n)$ n lois exponentielles indépendantes de paramètres respectifs $(\lambda _{i},1\leq i\leq n)$ : $X_{i}\sim {\mathcal {E}}(\lambda _{i})$ .

Les paramètres de mélange sont notés $(p_{i},1\leq i\leq n)$ et vérifient

\sum _{i=1}^{n}p_{i}=1,

Alors la loi de $Y$ peut être obtenue de la manière suivante : on tire avec probabilité $p i$ le paramètre $\lambda _{i}$ que l'on prendra pour la loi exponentielle ${\mathcal {E}}(\lambda _{i})$ que suivra $Y$ . On obtient ainsi une loi hyper-exponentielle de paramètres n, ( $p i$ ), ( $\lambda _{i}$ ). Cette loi sera notée : $Y\sim {\mathcal {H}}_{n}((p_{i}),(\lambda _{i}))$ .

Caractéristiques

La densité de probabilité de la loi hyper-exponentielle est la somme des densités des lois exponentielles :

f_{Y}(y):={\begin{cases}\sum _{i=1}^{n}p_{i}\lambda _{i}\mathrm {e} ^{-\lambda _{i}y}&{\text{ si }}y>0\\0&{\text{sinon.}}\end{cases}}

La fonction de répartition est donnée par :

F_{Y}(y):={\begin{cases}1-\sum _{i=1}^{n}p_{i}\mathrm {e} ^{-\lambda _{i}y}&{\text{ si }}y>0\\0&{\text{sinon.}}\end{cases}}

L'espérance est la somme pondérée des espérances des lois exponentielles :

\mathbb {E} (Y)=\sum _{i=1}^{n}{\frac {p_{i}}{\lambda _{i}}}

Applications

Puisque la loi exponentielle permet de simuler le temps de vie d'équipements en série, la loi hyper-exponentielle permet de simuler le temps nécessaire jusqu'à la prochaine réparation d'un système d'équipements en série lorsque le temps de vie peut être très court ou très long[2].

En remplaçant l'idée de panne d'un appareil par l'idée plus générale d'un évènement, par exemple l'arrivée d'un client ou d'un appel téléphonique, la loi hyper-exponentielle modélise le temps d'attente jusqu'au prochain appel dans un centre d'appel contenant n serveurs.

Liens avec d'autres lois

Si n=1, alors la loi hyper-exponentielle ${\mathcal {H}}_{1}(1,\lambda )$ est la loi exponentielle ${\mathcal {E}}(\lambda )$ .
Au même titre que la loi exponentielle est l'équivalent continu de la loi géométrique, la loi hyper-exponentielle est l'équivalent continu de la loi hypergéométrique.

Références

Pierre-Jean Erard et Pontien Déguénon, Simulation par évènements discrets, Lausanne/Paris, Presses polytechniques et universitaires romandes, 1996, 1^re éd., 425 p. (ISBN 2-88074-295-1, lire en ligne), p. 272
(en) A.K.S. Jardine, Operational research in maintenance, Manchester university press, 1970, 233 p. (lire en ligne), p. 22

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.