Loi hypo-exponentielle

En théorie des probabilités et en statistique, la loi hypo-exponentielle ou loi d'Erlang généralisée[1] est une loi de probabilité continue, à support semi-infini qui trouve des applications dans les mêmes domaines que la loi d'Erlang : théorie des files d'attente, ingénierie de trafic, etc. Le terme hypo vient du fait que le coefficient de variation de la loi est inférieur à un, comparativement à la loi hyper-exponentielle dont le coefficient de variation est supérieur à un et à la loi exponentielle dont le coefficient vaut un.

Loi hypo-exponentielle
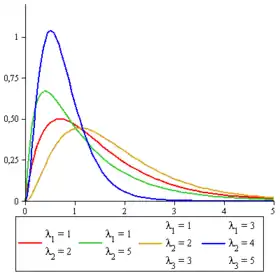Densité de probabilité


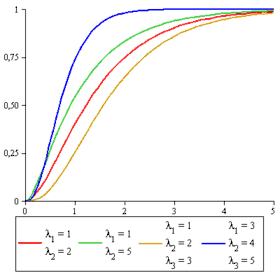Fonction de répartition

Paramètres	n=1,2,... $\lambda _{i}>0$
Support	$x\in [0;\infty [\!$
Densité de probabilité	$\sum _{i=1}^{n}\prod _{j\neq i}{\frac {\lambda _{j}}{\lambda _{j}-\lambda _{i}}}\lambda _{i}\mathrm {e} ^{-\lambda _{i}x}$
Fonction de répartition	$1-\sum _{i=1}^{n}\prod _{j\neq i}{\frac {\lambda _{j}}{\lambda _{j}-\lambda _{i}}}\mathrm {e} ^{-\lambda _{i}x}$
Espérance	$\sum _{i=1}^{k}1/\lambda _{i}\,$
Médiane	$\ln(2)\sum _{i=1}^{k}1/\lambda _{i}\,$
Mode	$0$
Variance	$\sum _{i=1}^{k}1/\lambda _{i}^{2}$
Asymétrie	$\sum _{i=1}^{n}{\frac {1}{\lambda _{i}^{2}}}$

Une variable aléatoire qui suit une loi hypo-exponentielle sera notée : $Y\sim \mathrm {Hypo} (\lambda _{1},\dots ,\lambda _{n})$ .

Définition

La loi hypo-exponentielle définie comme la loi de la somme de n variables aléatoires ${\textstyle X_{i},\,i=1,\dots ,n}$ de loi exponentielle indépendantes de paramètres respectifs : ${\textstyle \lambda _{i},\,i=1,\dots ,n}$ :

Y=\sum _{i=1}^{n}X_{i}

avec

X_{i}\sim {\mathcal {E}}(\lambda _{i})

Le coefficient de variation minimum de la loi hypo-exponentielle est $1/n$ .

Densité de probabilité

La densité de probabilité de la loi hypo-exponentielle se calcule par récurrence[2] pour obtenir la formule :

f_{X}(x)={\begin{cases}\displaystyle \sum _{i=1}^{n}\prod _{j\neq i}{\frac {\lambda _{j}}{\lambda _{j}-\lambda _{i}}}\lambda _{i}\mathrm {e} ^{-\lambda _{i}x}&{\text{ si }}x>0\\0&{\text{ sinon }}\end{cases}}

dans le cas où les paramètres ${\textstyle \lambda _{i}}$ sont tous différents deux à deux.

Fonction de répartition

La fonction de répartition de la loi hypo-exponentielle est donnée par[2] :

F_{X}(x)={\begin{cases}\displaystyle 1-\sum _{i=1}^{n}\prod _{j\neq i}{\frac {\lambda _{j}}{\lambda _{j}-\lambda _{i}}}\mathrm {e} ^{-\lambda _{i}x}&{\text{ si }}x>0\\0&{\text{ sinon }}\end{cases}}

avec le même critère pour le paramètres ${\textstyle \lambda _{i}\;:\;\lambda _{i}\neq \lambda _{j},{\text{ si }}i\neq j}$ .

Références

(en) Melania Calinescu, Forecasting and Capacity Planning for Ambulances Services, Amsterdam, rapport interne, 2009, 19 p. (lire en ligne), p. 10
(en) Sheldon Ross, Introduction to Probability models, Elsevier, 2010, 10^e éd., 784 p. (ISBN 978-0-12-375686-2, lire en ligne), p. 308

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.