Loi de Xenakis

La loi de Xenakis est la loi d'une variable aléatoire positive, utilisée par Iannis Xenakis en musique stochastique, par exemple pour les durées des notes et leur variation de hauteur[1].

Loi de Xenakis
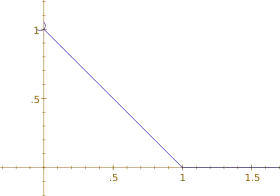Densité de probabilité Densité de la loi de Xenakis de paramètre 1


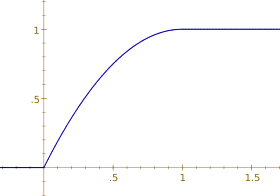Fonction de répartition Fonction de répartition de la loi de Xenakis de paramètre 1; elle est proche de celle d'une loi exponentielle de paramètre e

Paramètres	$\scriptstyle a>0$
Support	$x\in [0,a]$
Densité de probabilité	$\scriptstyle {\frac {2}{a}}\left(1-{\frac {x}{a}}\right)$ pour $\scriptstyle x\in [0,a]$
Fonction de répartition	${\frac {2ax-x^{2}}{a^{2}}}$ pour $\scriptstyle x\in [0,a]$
Espérance	${\frac {a}{3}}$
Médiane	$a\left(1-{\frac {\sqrt {2}}{2}}\right)$
Mode	0
Variance	${\frac {a^{2}}{18}}$
Asymétrie	${\frac {2{\sqrt {2}}}{5}}$
Kurtosis normalisé	$-{\frac {3}{5}}$
Entropie	${\frac {3}{2}}$
Fonction génératrice des moments	${\frac {2(e^{at}-at-1)}{t^{2}a^{2}}}$
Fonction caractéristique	${\tfrac {2-2\cos \left(at\right)+e^{-ita}-e^{iat}+2iat}{t^{2}a^{2}}}$

Définition

La loi de Xenakis est la loi de la longueur d'un segment inclus dans un segment de longueur $a$ [2]. C'est donc une loi triangulaire de paramètres 0, $a$ et 0.

Propriétés

Densité

La densité de la loi de Xenakis est, dans sa forme standard, une fonction affine sur $[0 , a]$ s'annulant en $a$ .

p(x)={\begin{cases}{\frac {2}{a}}\left(1-{\frac {x}{a}}\right)&{\text{ si }}x\in [0,a]\\0&{\text{ sinon.}}\end{cases}}

Le paramètre $a$ est donc un paramètre d'échelle ; la forme standard de la loi de Xenakis ne présente pas de paramètre de position.

Fonction de répartition

La fonction de répartition de la loi de Xenakis est du second degré. Par conséquent, on peut simuler celle-ci à l'aide d'une loi uniforme continue. En effet, si $X$ est une variable aléatoire uniforme sur $[0 ; 1]$ , $a\left(1-{\sqrt {1-X}}\right)$ est une variable aléatoire de Xenakis de paramètre $a$ .

F(x)={\begin{cases}0&{\text{ si }}x<0\\1-{\frac {(x-a)^{2}}{a^{2}}}&{\text{ si }}x\in [0,a]\\1&{\text{ si }}x\geqslant a.\end{cases}}

Loi de Xenakis de paramètres affines fixés

Loi de Xenakis de paramètre 1

La loi de Xenakis sur $[0 ; 1]$ est une loi bêta de paramètres 1 et 2. On peut donc définir la loi de Xenakis de paramètre 1 comme la loi du minimum de deux variables aléatoires uniformes sur $[0 ; 1]$ .

Loi de Xenakis centrée réduite

La loi de Xenakis centrée réduite, donc d’espérance 0 et d’écart type 1, est définie sur $[-{\sqrt {2}};2{\sqrt {2}}]$ par :

p(x)={\frac {2{\sqrt {2}}-x}{9}}

Distributions associées

Le minimum de deux variables aléatoires de Xenakis de paramètre 1 suit une loi bêta de paramètres 1 et 4.

Simulation

Pour simuler une variable de Xenakis de paramètre 1 à partir de variables uniformes sur $[0 ; 1]$ , on a le choix entre trois méthodes:

la définition, en rappelant que la distance entre deux nombres est la valeur absolue de leur différence ;
Le fait qu'une variable de Xenakis est une variable de loi bêta, le minimum de deux nombres étant assez rapide à calculer (cette façon de faire n'était apparemment pas connue de Xenakis) ;
l'utilisation de l'inverse de la fonction de répartition, qui est d'ailleurs celle utilisée par Xenakis[3].

Notes et références

Iannis Xenakis, Musiques formelles : nouveaux principes formels de composition musicale, Paris, Stock/Musique, 1981, 260 p. (ISBN 2-234-01510-3, BNF 36143274), Annexe
Musiques formelles, chapitre 1
Musiques formelles, appendice

« Musiques formelles », sur http://www.iannis-xenakis.org (consulté le 9 octobre 13)

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.